Section 9.5: Differences Between Several Independent Groups: The Kruskal–Wallis Test
Learning Objectives
At the end of this section you should be able to answer the following questions:
- What is the parametric antilog to the Kruskal-Wallis Test?
- What test would you use to compare differences between several related groups?
The Kruskal-Wallis H test for three or more Independent Samples
When examining the differences between three or more groups, Kruskal-Wallis H Test is best. This test examines the differences in median scores, as well as the size of the differences. This test examines the main effect of your variable, similar to an ANOVA. Example: Is there a difference in the median reported levels of mental distress for full-time, part-time, and casual employees? If one wanted to compare differences between several related groups, the test to use would be Friedman’s ANOVA.
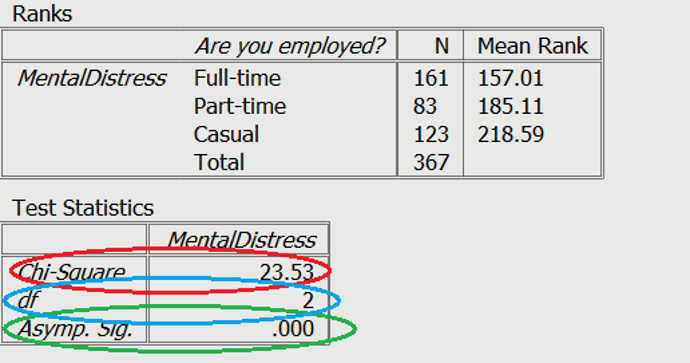
Interpretation of the Kruskal-Wallis H test
As can be seen in the blue, there is a statistically significant difference, note the p value. The chi-squared value, and degrees of freedom are also needed for reporting. The median ranks indicate that casual employees have the highest scores of mental distress. It is important to note that follow-up tests are required for individual group differences (like Mann-Whitney U Tests), similar to posthoc tests in ANOVA.
Write-up
A Kruskal-Wallis H test showed that there was a statistically significant difference in levels of mental distress, χ2(2) = 23.53, p < .001, for full-time (Median = 157.01) , part-time (Median = 185.11) , and casual employees (Median = 218.58).
PowerPoint: Kruskal Wallis
Please click on the slides below to see an example of interpretation for the Kruskal-Wallis H test.

