2.1 Datums and Coordinates
Learning Objectives
After successfully completing this chapter you should be able to:
- identify and describe the essential elements of ellipse geometry
- differentiate between the ellipsoid and geoid and identify when measurements relate to each of these
- define and compare common horizontal and vertical datums in use today
- outline the history of the development of these datums
- explain the fundamental characteristics of the Australian Height Datum (AHD)
- demonstrate an understanding of the construction and use of geoid models
- apply values from geoid models to attain orthometric heights from GNSS surveying observations.
In the beginning…
A guy looked down a well.
What came next
Eratosthenes was a Greek mathematician, geographer, poet, astronomer and librarian. He was the first known person to calculate the circumference of the Earth, in around 240BC. And he did it all without leaving his home in the city of Alexandria.
Eratosthenes knew that at noon on the summer solstice, in what is now known as Aswan in Egypt, if a person was standing over a well their shadow would block the reflection of the Sun on the water in the well. At the same time in Alexandria, he measured the shadow of a rod on the ground. Using the well-known distance between Aswan and Alexandria (which was surveyed every year) he combined this information with some simple geometry to determine the circumference of the Earth. He didn’t get it exactly right, but given the technology of the day, he did a pretty good job!
Armed with this knowledge, Eratosthenes published a three-volume work called Geographika, and created the science we now know as Geography. Geographika contained the first model of the Earth that was covered with the grid we now recognise as latitude and longitude.
You can watch the NASA video explaining the history and applications of geodesy below.
Video 2.1: Looking down a well – a brief history of geodesy [2 mins, 25 secs]
Note: Closed captions are available by clicking the CC button in the clip below. This video is in the Public Domain.
Due to his enormous contributions to the field, Eratosthenes is often referred to as the Father of Geography.
All because some guy looked down a well.
The field of geodesy
Our understanding of the size and shape of the Earth has become known as geodesy, from the Greek word ge (earth) and daiein (divide).
The Offshore Petroleum Amendment (Datum) Bill defines geodesy as:
“The branch of applied mathematics which determines the shape and area of large tracts of country, the exact position of geographical points, and the curvature, shape, and dimensions of the earth.”
The surface of the Earth is very irregular, so when we measure things on the surface, we need to show them relative to some standard surface. A critical component of geodesy is developing these standard surfaces; mathematical models that represent the size and shape of the earth.
Ellipsoids
In the 17th century, Sir Isaac Newton reasoned that the surface of the Earth could best be represented by the surface of the oceans, but due to the rotation the Earth, the effect of centrifugal forces on the liquid oceans would make them bulge at the equator.
Measurements by geodesists proved this to be the case, showing that the Earth is about 43km wider at the equator than pole to pole, which is about 1/300 of the diameter.
This means that the Earth is not a perfect sphere, but an oblate ellipsoid.
The easiest way to visualise an oblate ellipsoid is to imagine what happens to a slightly flat soccer ball (or other ball that takes your fancy) that someone is sitting on. Ellipsoids can be described mathematically, as they have standard geometry.
Oblate means that a round shape has been flattened along the z axis. In the world of astronomy, this is the axis of rotation of the planet or other astronomical body.
Prolate means that the round shape has been flattened along the x & y axes, much like an AFL Sherrin football.
Ellipsoid geometry
An ellipsoid provides a simple mathematical approximation for the shape of the earth, either regionally or globally. The ellipsoid is a surface of revolution generated by rotating an ellipse about its minor (shortest) axis.
Figure 2.1(a) shows a typical ellipsoid and the geometric meaning of the parameters that define its size and shape
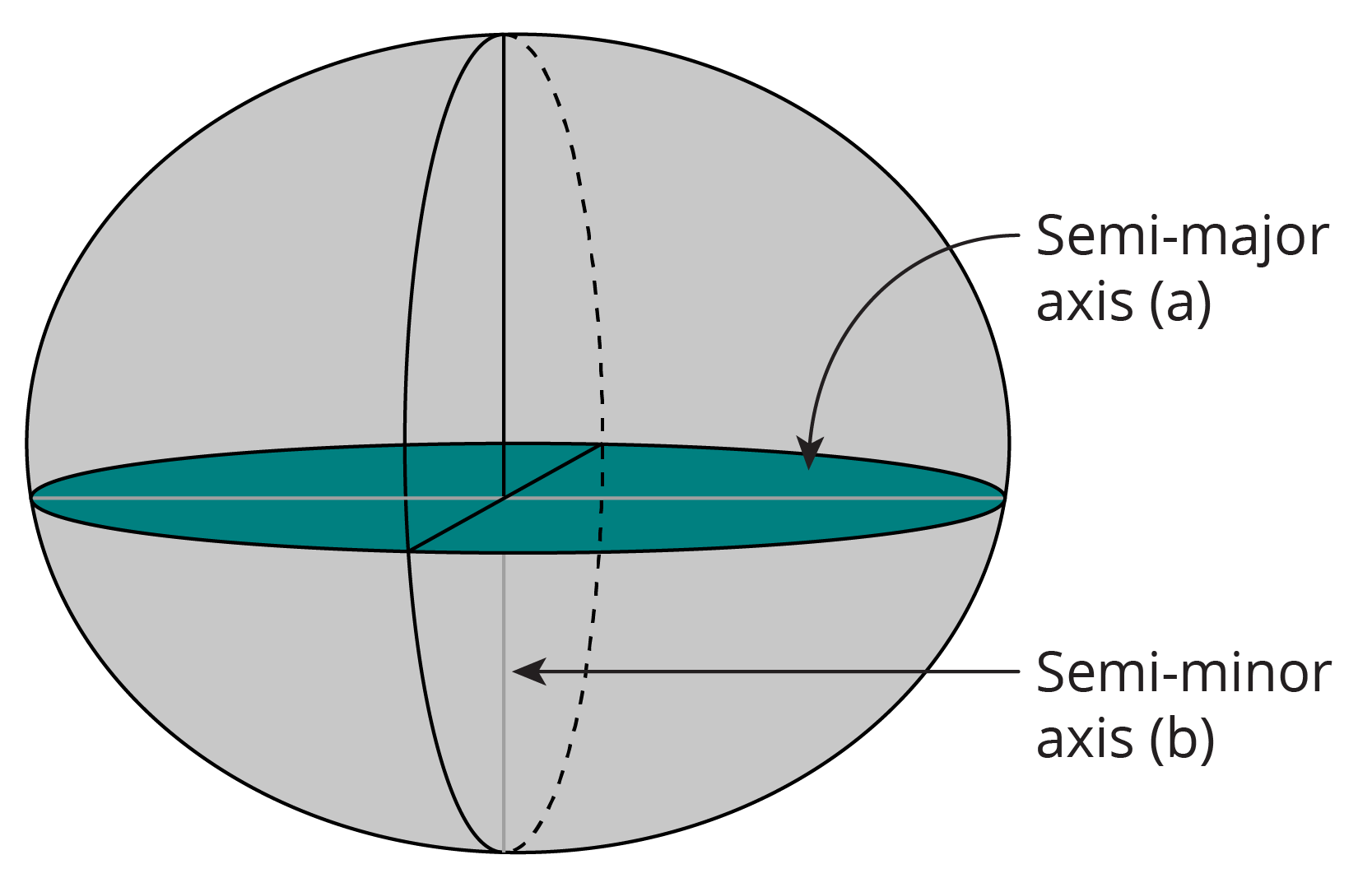
a = major semi axis of the ellipse
b = semi minor axis of the ellipse
f = flattening (approx ![]() for Earth).
for Earth).
The flattening determines the amount by which the ellipsoid is ‘flattened’ along the semi minor axis, which for the Earth is the axis of rotation. The flattening is defined by the equation:
![]()
The flattening is essentially a ratio of the two axes, so it has a value range of 0 to 1 where a value of zero would mean the two axes are equal (as in the case of a sphere).
Only two parameters are necessary to define the size and shape of a reference ellipsoid, and usually the parameters chosen are the length of the semi major axis and the inverse flattening (1/f).
The inverse of flattening is normally used when referring to ellipsoids to do with the Earth, as the flattening of the Earth is quite a small number: 0.003353.
As an ellipsoid is a mathematical model, it can never be directly measured, however, we are able to measure things relative to it.
The geoid
When we measure points on the irregular surface of the Earth, we need to show them relative to a reference surface, which as we have just discussed, can be mathematically defined by an ellipsoid.
However, this requires us to ‘reduce’ them from the location we took the measurement, to the reference surface, which can be quite time consuming, particularly without the benefit of modern day calculators and computing power. An obvious choice of a common surface that could be used everywhere was the sea level surface.
The level of the oceans at any given point on the earth is determined by the force of gravity that keeps the oceans from flying off into outer space. Gravity is a function of mass, and since the material of which the earth is made is not of uniform density, the sea level deviates from a regular ellipsoid shape from place to place.
The inconsistent density of the Earth is due to land masses, deep sea trenches and other materials. This means the exact shape of the earth, as indicated by the level of the oceans, can only be described as a ‘blob’. It does not conform to any regular mathematical formula or regular geometric shape. Since this terminology is not very scientific or aesthetically pleasing, geodesists invented a new shape and they gave this new shape the name geoid.
Because sea level is affected by gravity, the geoid is considered an equipotential surface, meaning it is perpendicular to gravity everywhere, as shown in Figure 2.1(b) The geoid extends worldwide, across the continental land masses.
It is important to note the geoid only considers the influences of the Earth’s own rotation and gravity on sea level, ignoring all other influences, like the impact the moon and winds have in creating tides.
The geoid and heights
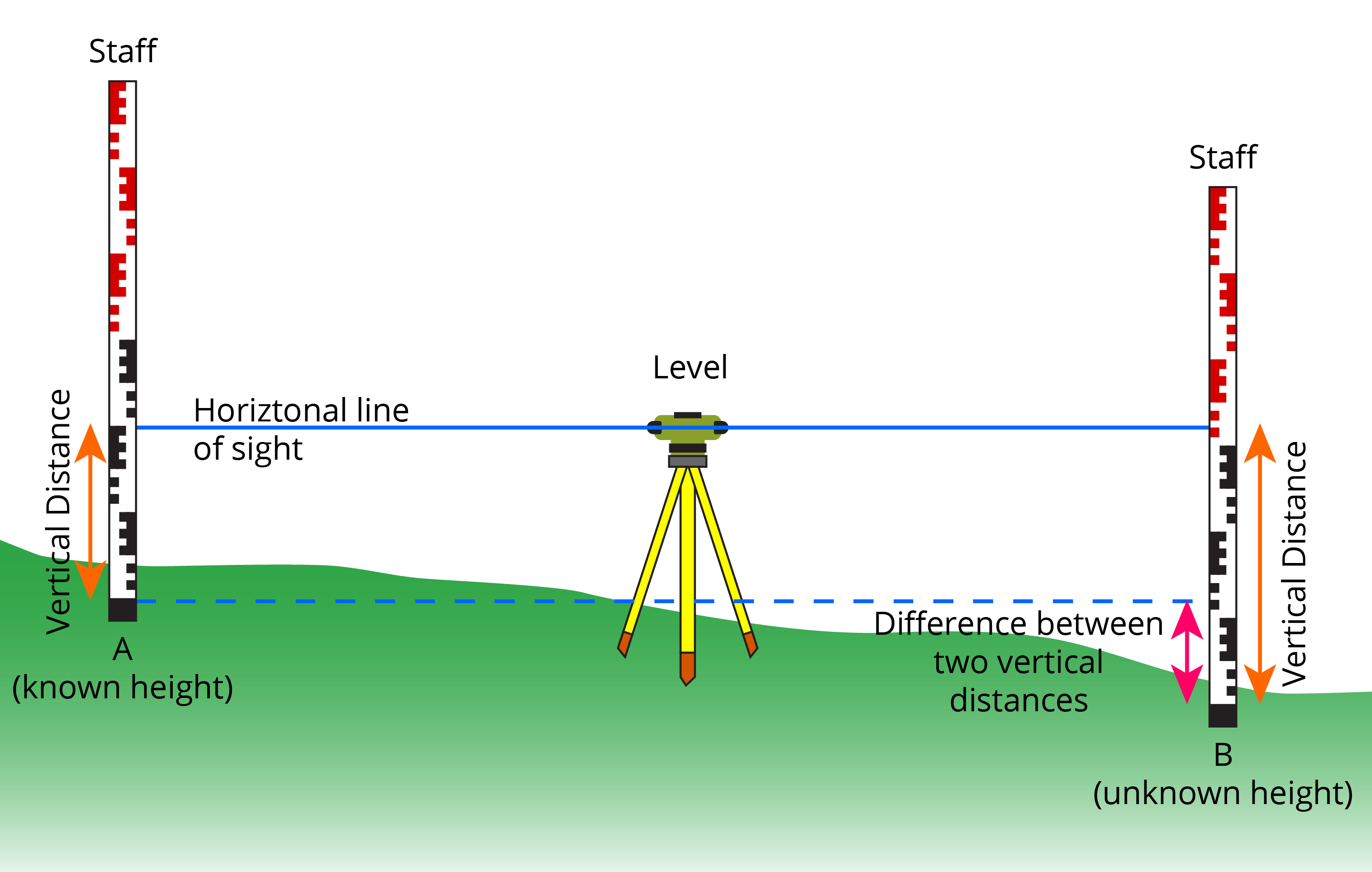
As the geoid is an equipotential surface, this means that it is defined by gravity. The benefit of gravity and the geoid is in measuring heights. We can use a surveying technique called levelling to measure the differences in heights between places, as shown in Figure 2.1(c).
While the variation in the Earth’s surface, called the topography, ranges from -11,034m in the Marianas Trench to +8,848m at Mt Everest, the deviation of the geoid from a global ellipsoid only ranges from approximately +85m in Iceland to -106m in India. So, while the geoid is an undulating surface due to changes in gravity, it is considerably more regular than the Earth’s physical surface.
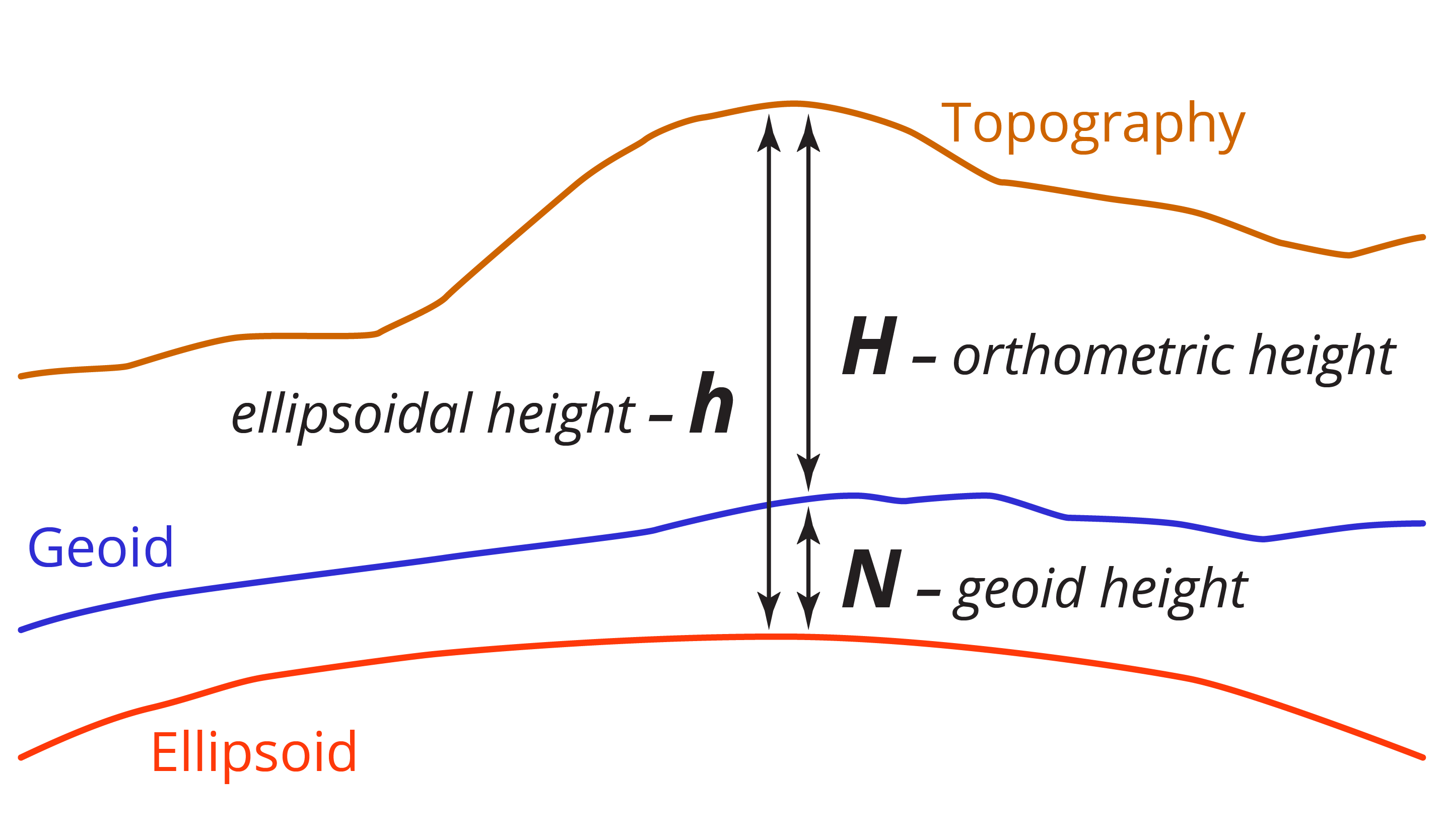
The deviation of the geoid from the ellipsoid will change at different locations, and is called the geoid-ellipsoid separation, and is represented by N. It is sometimes referred to as the geoid height.
But alas, measuring the topography of the Earth is what we need to do, and the geoid provides a reference surface that we can measure heights relative to. The distance from the geoid to the topography of the Earth is known as the orthometric height, and is represented by the symbol H. The distance from the ellipsoid to the topography is known as the ellipsoid height and is represented by the symbol h. The relationship between the three heights can be shown by the equation:
H = h -N
Where H = orthometric height
h = ellipsoid height
N= geoid – ellipsoid separation or geoid height
This relationship is shown in Figure 2.1(d).
When calculating the different heights, it is critical that the user understands which surface they are measuring to, and particularly which ellipsoid they are using.
A warning note: If we use ellipsoid heights in some situations (like engineering design) instead of geoid heights, we can end up in a situation where we are trying to get water or fluids to flow uphill!
Geoid models
As gravity is different across the globe, it is common for countries and regions to produce their own geoid model, where various scientific methods are used to approximate the geoid, most often by observing gravity using gravimeters, or by observing mean sea level (MSL). The later technique is discussed further in the section of this module on height datums. The critical component of a geoid model is the value of the difference between the geoid and the ellipsoid.
The geoid and horizontal positions
However convenient the geoid might initially appear to be as a reference surface, particularly for its very close approximation to sea level, it is unsuitable as a reference surface for horizontal positions.
The use of an ellipsoid that most nearly matches the topographic surface of the earth (or the geoid), to which calculations can be related is required. Such models of the surface of the earth are called geodetic datums and can be used in navigation, surveying and mapping.
Geodetic datums
A datum is also called a reference surface or reference system. It provides a model that lets people measure locations on the Earth’s surface, relative to a particular ellipsoid that best fits the country, region or continent where the measurements are taking place, at a particular point in time.
There are three main parts to a geodetic datum as shown in Figure 2.1(e); the ellipsoid, epoch and reference frame (which is also called a realisation).
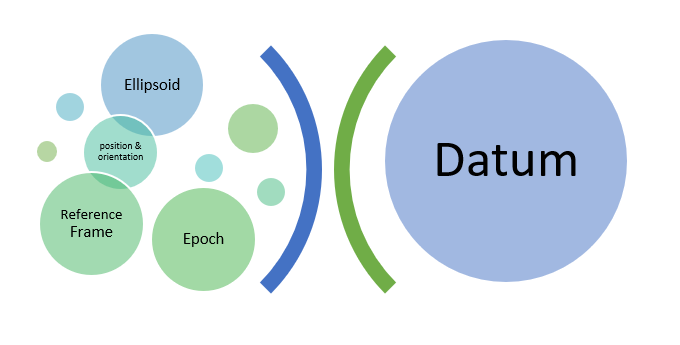
The ellipsoid has the usual ellipsoid geometry properties of semi minor and semi major axes, as well as flattening, that define its shape but also needs to have a position and orientation, which are determined by the reference frame.
The position of the ellipsoid refers to where its centre (or origin) is relative to the Earth, and the orientation refers to the axis of rotation. The axis of rotation is determined by the location of the north and south poles and the equator, which subsequently determines how the lines of latitude and longitude are orientated.
A reference frame, or realisation is where physical measurements at known points on the Earth are taken to determine the position and orientation of the ellipsoid. The realisation commonly use known points that are known in surveying as permanent marks, which are physical survey marks that are maintained by various State and Territory governments in Australia.
Datums are also referenced to a point in time, called an epoch. This essentially means that the parameters for that datum were defined at this date, and any measurements made on that datum are relative to the positions at that point in time. The epoch is the third of the three components that define a datum.

There are many different datums, and they are all uniquely named. An example is the global datum developed for GPS, called the World Geodetic System of 1984, shortened to WGS84. The two parts that make up the name are explained in Figure 2.1(f).
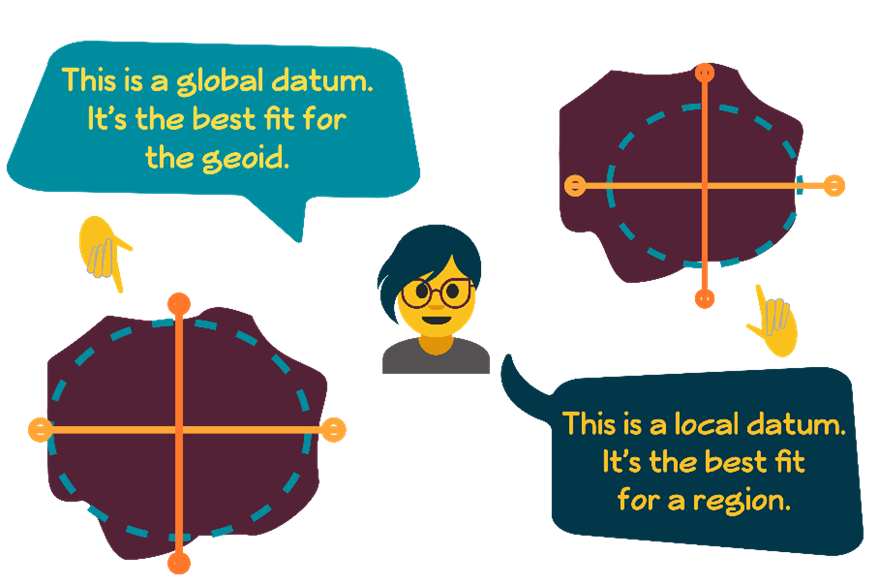
Before technology like GNSS, local and regional models were very common, as there was no real need to relate data on a global scale. These datums are called local datums, and have huge variations in their ellipsoid geometry, position and orientation.
Once GPS arrived, a global datum was needed – a datum that was the best fit for the geoid in a global sense. Figure 2.1(g) shows the concepts of local and global datums.
GNSS and Geocentric datums
Because satellites are affected by Earth’s gravity field, their orbits are related to the centre of mass of the earth (we will cover orbits in Chapter 3 when we discuss Kepler’s laws of planetary motion).
This means that calculations of the positions of satellites need to be referred to a datum based on the earth’s centre of mass. Datums that are centred on the centre of mass of the earth are known as geocentric datums.
A geocentric datum provides direct compatibility with GNSS measurements and mapping that is based on a geocentric datum
Ideally we would like a single ellipsoid, or one worldwide standard, that best represents the entire globe, so for world-wide applications and to achieve compatibility with GPS, it was decided to define a geocentric datum. This ellipsoid would provide a best fit of the earth on a global scale. Today, the GPS datum is WGS84 (World Geodetic System of 1984) and the GRS80 (Geodetic Reference System of 1980) ellipsoids are the ones preferred by surveyors and cartographers worldwide and represent the best fit of the entire geoid in a global sense.
Since any ellipsoid is only a best fit to the geoid: just how good is this best fit? WGS84 is approximately 60 metres above and 100 metres below the geoid in Australia. Since the radius of the earth is about six million metres, the maximum deviation of the ellipsoid and the geoid is about one part in 100 000.
Note that since the WGS84 ellipsoid represents a best fit for the entire earth, a local datum would provide deviations significantly smaller than these maximums.
Height datums
Generally, an approximation of Mean Sea Level (MSL) is used to make height datums, as MSL can be considered an approximation of the geoid. MSL is observed through a network of tide gauges – currently 19 years is understood as the appropriate amount of time for data to be collected to determine MSL.
Permanent survey marks, known as benchmarks are installed near the tide gauges, and the height (relative to MSL) is transferred from the gauge to the marks by surveying levelling techniques. The ‘level’ or height above MSL is assigned to the mark, and this is used to determine the level of other marks across land.

