Most GNSS chips available in devices like smartphones, tablets and in car systems, only use the L1 GPS signal for positioning. These types of receivers are called single frequency receivers. They use the code observable – the PRN codes, C/A and P(Y), on L1 to obtain a position of a point quickly and in three dimensions, using just one GNSS receiver.

This is where we get the name point positioning from; it is the fastest, cheapest, easiest, but least accurate method of GNSS positioning.

The basics of point positioning

By now, we have covered the basics of how GNSS works, so you should be aware that the time GNSS signals (radio waves) take to get from a satellite to a GNSS receiver are a critical component of measuring the distance from a satellite to a GNSS receiver. This distance is referred to as a range, and taking these measurements is referred to as ranging.

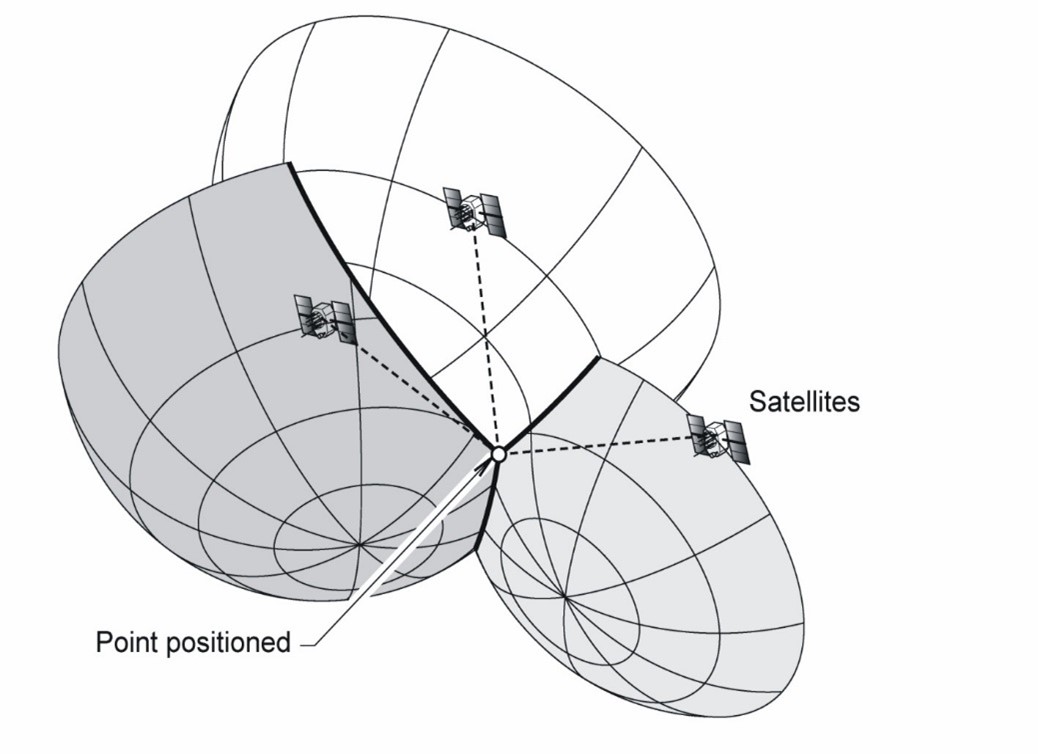
We’ve also briefly covered the fact you need a minimum of four satellites to get a position using GNSS, but why is this?

Well, it’s essentially trilateration over some big distances, plus correcting for clock errors using the satellite ranges. Let’s look at this in more detail.

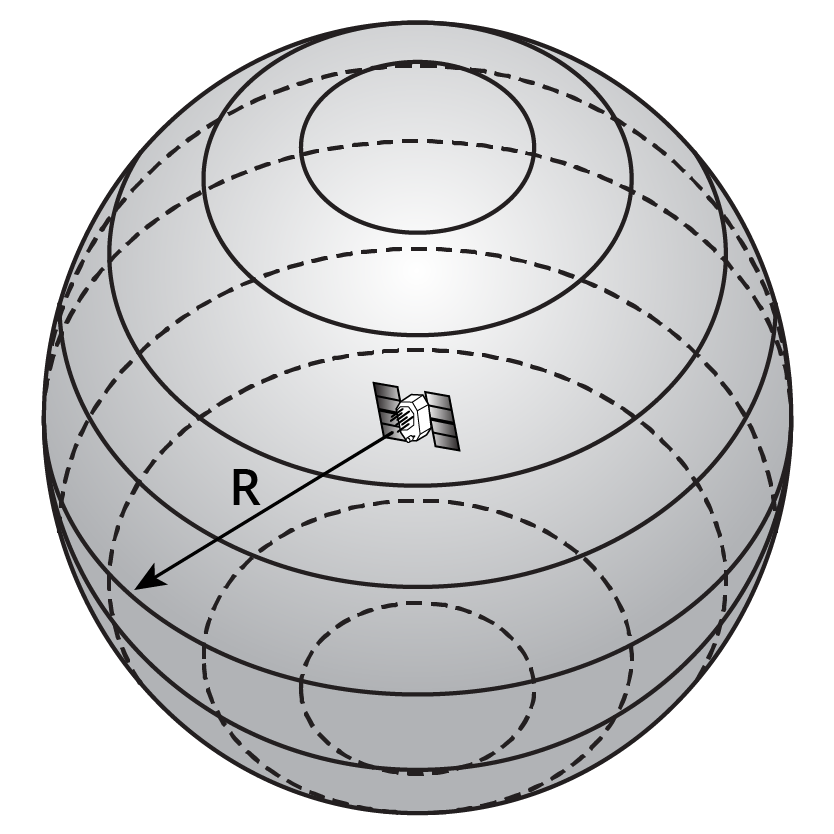
We can measure a satellite range by knowing the amount of time the GNSS signal takes to get to our receiver, but if we can only determine one satellite range, all this really means that we’re somewhere on a sphere with a radius of approximately 20,000km, as shown in Figure 4.2(a). This isn’t particularly useful on its own!

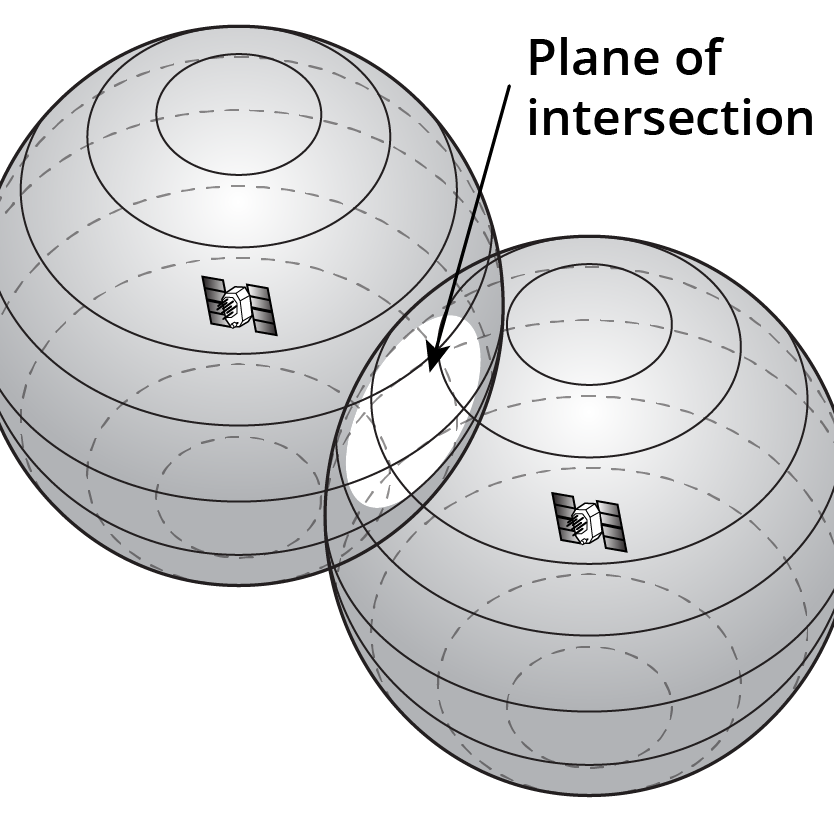
By adding in a second satellite range, we now have two spheres of similar radius that have an intersecting plane. We know we’re somewhere on the circle where the two spheres intersect, as shown in Figure 4.2(b).

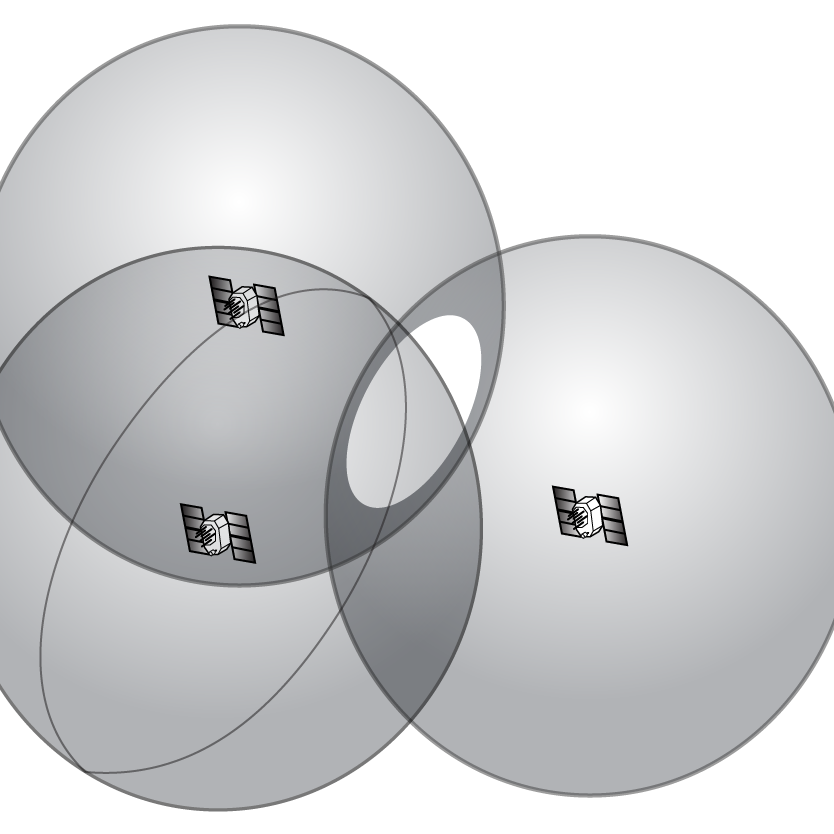
The third satellite range gives us a third sphere, and now we’re down to two possible spots on the circle where the first two spheres intersect, as shown in Figure 4.2(c).

Adding in satellite range number four means we can eliminate one of the two points, as shown in Figure 4.2(d) and now we have a point position in an ECEF coordinate system.

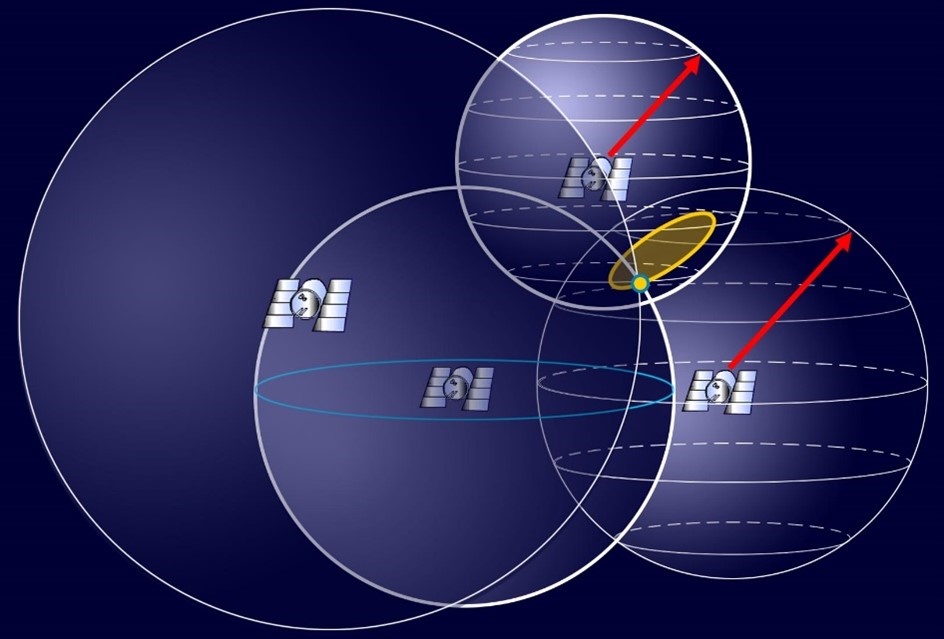
In reality though, our receiver can figure out our position with only three satellite ranges, as one of these points is going to be nowhere near the Earth. The GNSS receiver has various techniques it uses to allow it to figure out the correct point from the incorrect one. This is essentially how point positioning works, as shown in Figure 4.2(e).

If you know your elevation, you could also eliminate one of the satellite ranges and replace it with a sphere that has a radius of your distance from the centre of the Earth, but thankfully we no longer have to do this. So, what’s with needing the fourth satellite then?

We know there are errors in GNSS measurements due to receiver, location and system errors. The fourth satellite essentially acts as a check on the other three measurements, and helps us deal with clock errors. In point positioning we do this through a process called code pseudo range positioning.