Now we understand how to determine the motion or orbit of a satellite, the next step is to understand how we describe this relative to the Earth. As we learnt in Chapter 2, the best way to do this is using a coordinate system. To describe the position of satellites, we use an Earth centred, Earth fixed Cartesian coordinate system.

The system is defined by:

• centre of the Earth is fixed at (0, 0, 0)
• X axis aligns with the zero meridian, which is the first point of Aries, represented by y. This is the point of the Sun at the vernal equinox in the northern hemisphere, around 20th – 22nd March.
• Y axis is perpendicular to the X axis in the equatorial plane, also called the plane of the celestial equator
• Z axis is the mean axis of rotation for the Earth.

However, this isn’t enough information to fully describe the position of a satellite, as we need to understand how the orbit of a satellite is positioned relative to the Earth as well. We do this by using the six Keplerian elements that define an orbit.

Orbital elements

From Kepler’s laws, there are six elements or parameters that are needed to describe the position of a satellite, three of them we already know:

• Eccentricity of the ellipse
• The semi major axis
• The true anomaly

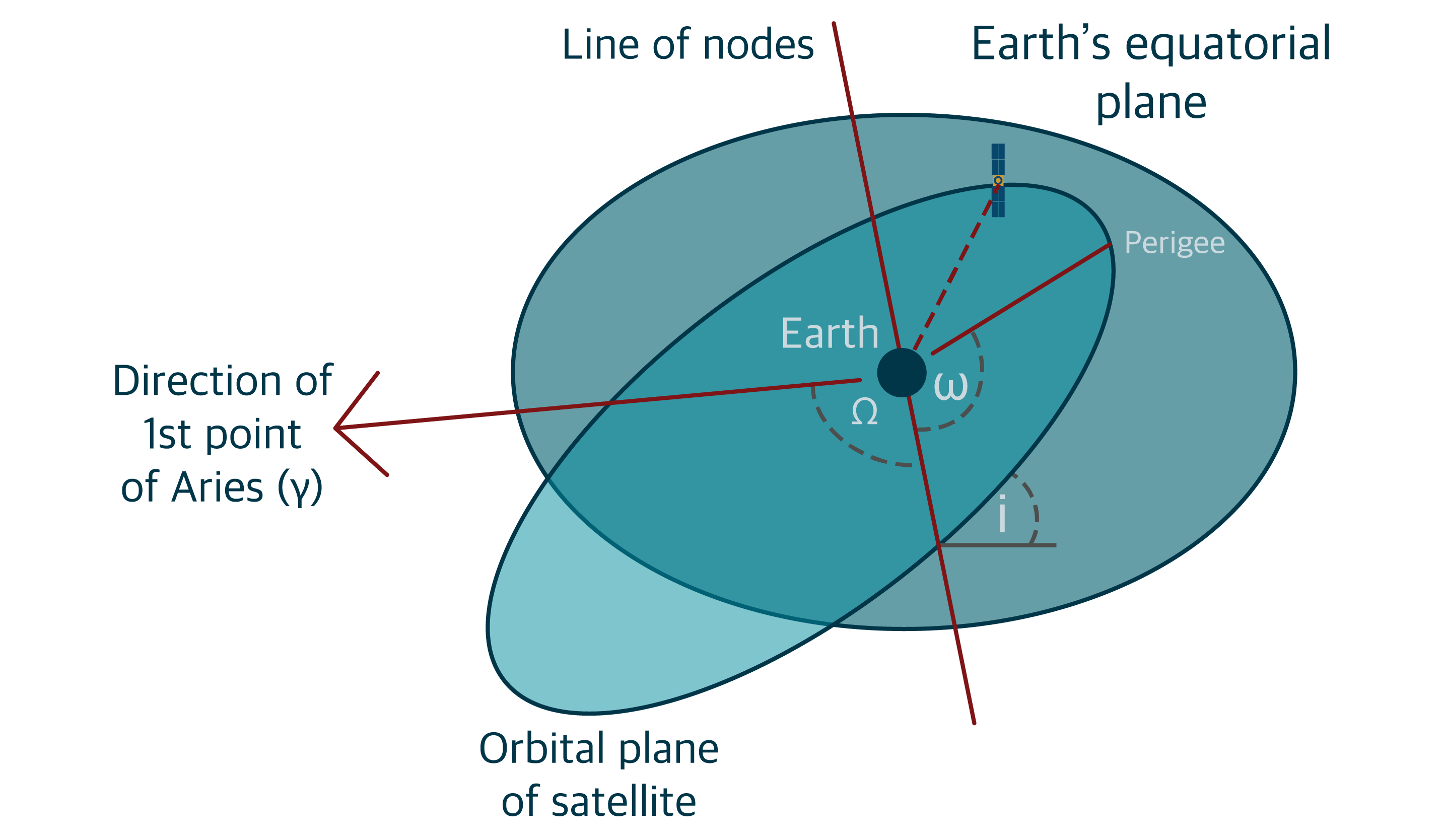
The remaining three are to do with how the satellite orbit is positioned relative to the Earth, and to do this we measure the three different angles between the orbital plane and the Earth’s equatorial plane. These are shown in Figure 3.3(a) In this figure:

• The line of nodes is the line where the two planes intersect. The edges of the orbital plane on this line are points called nodes; the ascending node and the descending node
• The first point of Aries is represented by the lowercase Greek letter gamma, . This is the point of the Sun at the vernal equinox in the Northern Hemisphere, around 20th – 22nd March

The three remaining elements are:

• The inclination of the orbital plane is the angle between the equatorial plane and the orbital plane, and is represented by i
• The longitude of the ascending node is the angle from the vernal equinox to the ascending node in the equatorial plane. It is represented by the uppercase Greek letter omega,
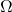
• The argument of the perigee is the angle from the line of nodes to the perigee in the orbital plane. It is represented by the lowercase Greek letter omega

These are shown in Figure 3.3(a).

Combining these three parameters with the ECEF Cartesian coordinate system, we are able to describe the position of a satellite around the Earth. BUT….

The Earth is an ellipse that isn’t homogenous – gravity, air resistance, radiation pressure from the Sun all impact the orbit of satellites. This means the Kepler elements are constantly changing, so our predictions of satellites’ orbits have to be constantly updated. This is where the ephemeris comes into play, but more on that later.

Satellite constellations

Now we have a good understanding of how the motion and position of satellites are measured, we can review the three main Global Systems of GNSS and their specific satellite configurations.

These are all correct at the time of writing, however, the number of functional satellites will vary due to decommissioning of older satellites, and the launch of new ones.

GPS

The GPS satellite constellation consists of a minimum of 24 operational satellites arranged in six orbital planes with four satellites in each plane.

Although the nominal GPS operational constellation consists of 24 satellites that orbit the earth in about 12 hours, there are often more than 24 operational satellites as new ones are launched to replace older satellites.

The orbit altitude is approximately 20,000km, and is such that the satellites repeat almost the same ground track and configuration over any point in just short of every 24 hours (actually about four minutes earlier each day).

There are six orbital planes (with nominally four SVs in each), equally spaced (60 degrees apart), and inclined at 55 degrees with respect to the equatorial plane. This constellation often provides the user with between five and eight GPS SVs visible from any point on the earth.

Galileo

The Galileo constellation has 22 operational satellites, with another two used for testing and two that are decommissioned. They are arranged in three orbital planes, with an inclination of 56°. The planes are designated as A, B and C, and each have eight ‘slots’ for satellites, all of which are currently filled.

Galileo satellites are at an altitude of 23 616km.

GLONASS

The GLONASS constellation has developed in two main phases;

• Initial development through to full constellation deployment happened during the 1970s and 1980s, with a decline in operations in the 1990s after the collapse of the Soviet Union. The satellites launched during this phase are all decommissioned.
• Since the late 1990s and early 2000s, led by the Russian Space Agency. The current constellation has 24 satellites, with an additional satellite under testing and several more commissioned.

The inclination of the GLONASS satellite orbital plane is 64.8° and there are three orbital planes. Satellites orbit at 19 100 km.