Humans have been observing celestial bodies and their motion since ancient times, with some of the earliest records dating back to around 1200 BC.

The term satellite is used in astronomy to describe an astronomical body (like a moon) that orbits a planet. They are also known as natural satellites since the invention of artificial satellites like those used in GNSS. Regardless of whether they’re natural or artificial, all satellite orbits are governed by a set of scientific laws, most commonly known as Kepler’s laws of planetary motion.

Johannes Kepler was a German mathematician and astronomer in the 17th century, and he published a series of works that outlined how the Earth and other planets orbited the Sun. His work built on the theories of Nicolaus Copernicus, who had suggested that planets orbited the Sun in circular orbits. Kepler realised that the orbits were actually elliptical and proposed three laws that explained how these orbits worked.

In GNSS, Kepler’s laws of planetary motion are used to predict the position of satellites, which is a critical component of positioning, and is included in the signals transmitted by GNSS satellites. This information is in the ephemeris, which we will discuss further in the signals section of this module.

We already know that ellipses are important to GNSS, and how to define them, the fact that satellites have an elliptical orbit makes it pretty easy to understand the maths in Kepler’s laws.

However, before we discuss Kepler’s laws, it’s helpful to get our heads around some basic astronomical terms that relate to elliptical orbits. Because we’re going to be talking about satellites orbiting the Earth, we’ll look at the basics from this perspective.

The basics of elliptical orbits

Kepler proved that the orbit, or path that a satellite took around a body, was an ellipse. As we already know, an ellipse is defined by the semi major (a) and semi minor (b) axes, as shown in Figure 3.2(a). The centre of the ellipse is represented by C.

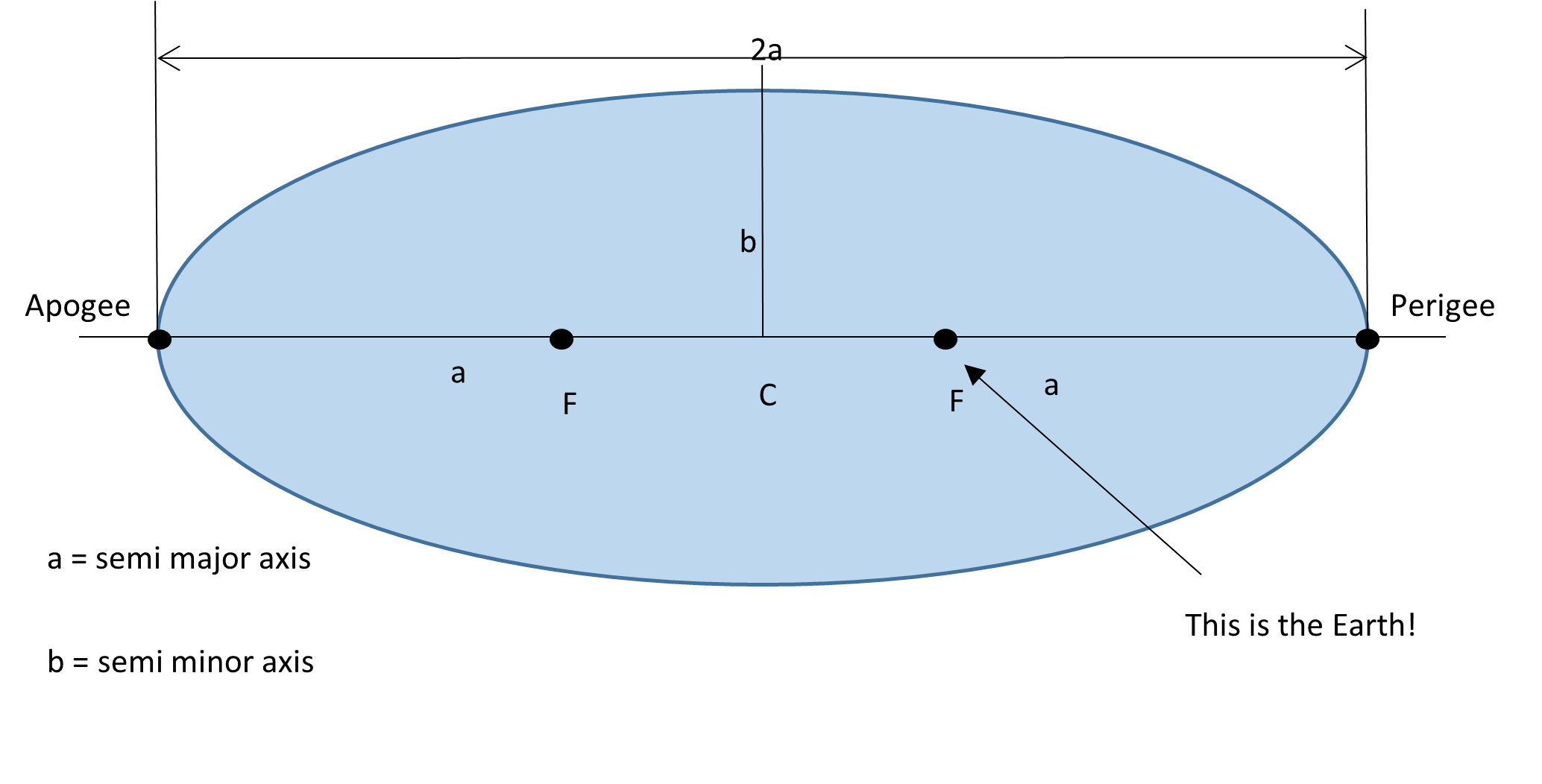
Perigee and apogee

The perigee and the apogee are points on the ends of the major axis, as shown in Figure 3.2(a). The prefix Peri means “near”, so the perigee is the closer of the two points to the Earth, while Ap means “away from”, so the apogee is the furthest point on the major axis from the Earth.

Depending on what the body being orbited is, depends on what these concepts are called. When orbiting the Sun we use the term “–hellion”, giving us aphelion and perihelion, while stars use “-astron” – apastron and periastron. The generic version is “-apsis”, giving apapsis and periapsis.

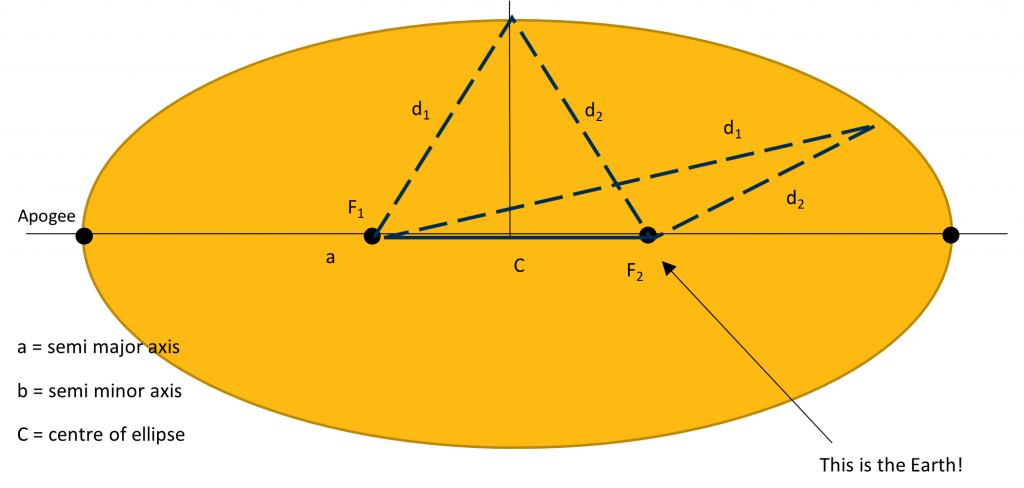
Foci

An ellipse also has two foci points (focus is the singular), represented by , as shown in Figure 3.2(b). The positions of the foci are such that at any point on the outside of the ellipse, the sum of the distances from that point to each of the foci will always be the same.

An easy way to visualise this is if you put two nails in a piece of wood a distance apart, and join them with a piece of string about two and a half times longer than the distance between them. If you pulled the string tight with a pencil and then moved it around 360 degrees, keeping the string tight, it would draw an ellipse. The total length of the string didn’t change, but the distance from each focus did. This is shown in Figure 3.2(b).

The distance from the centre of the ellipse to either of the foci is represented by

Eccentricity

How much an ellipse is away from being a circle is measured by its eccentricity. The distance between the two foci is defined in terms of eccentricity of the ellipse, which is represented by . Eccentricity is mathematical concept that has to do with conical sections, and for an ellipse, eccentricity will have a value greater than zero but less than one.

If you know where the centre of the ellipse is, the eccentricity is simply the distance from the centre to either of the foci, divided by the length of the semi major axis, given by the equation:

Eccentricity is important because it helps us calculate the position of satellites in their orbit relative to the Earth.

Kepler’s first law – the Law of Orbits

The Kepler’s first law, also known as the Law of Orbits states that the orbit of every planet will be an ellipse, with the centre of mass of the Sun being at one of the foci of the ellipse, as shown in Figure 3.2(a). Remember Kepler was talking in terms of our solar system, so he was describing how planets were orbiting the Sun. For GNSS, the equivalent is that satellites will have an elliptical orbit where the Earth is at one of the foci of the ellipse.

To calculate the x and y values in Kepler’s equation, we need to do some calculations to determine the position of a satellite in its orbit. The best way to understand this is through an example.

Let’s assume we have a satellite ‘S’ that is in an elliptical orbit around the Earth, as shown in Figure 3.2(c). We need to determine where the satellite is relative to the Earth, but as well as relative to its orbit. We can determine the  values from Kepler’s equation using our knowledge of plane coordinates, as shown in Figure 3.(c).

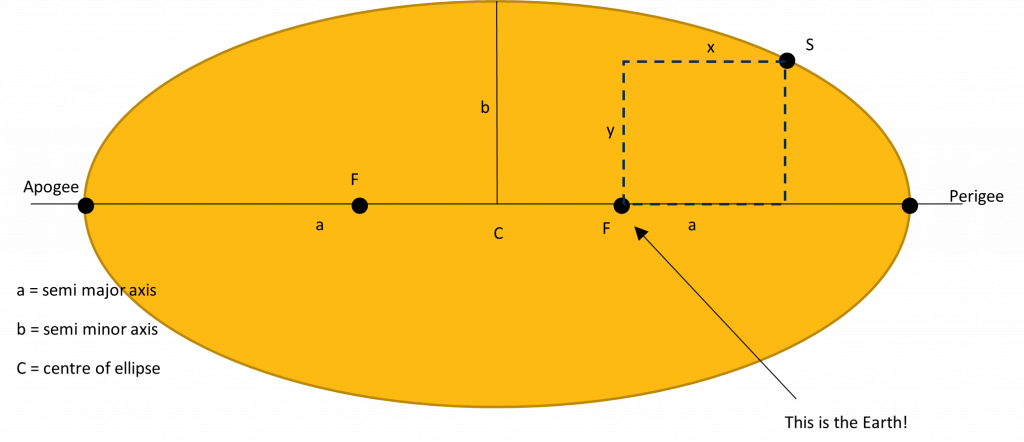
Next, we need to determine the angle between the satellite and the Earth, represented by the lowercase Greek letter phi, , and we’ll call the distance from the satellite to the Earth R (keeping in mind its value will change depending on where the satellite is in its orbit), as shown in Figure 3.2(d).

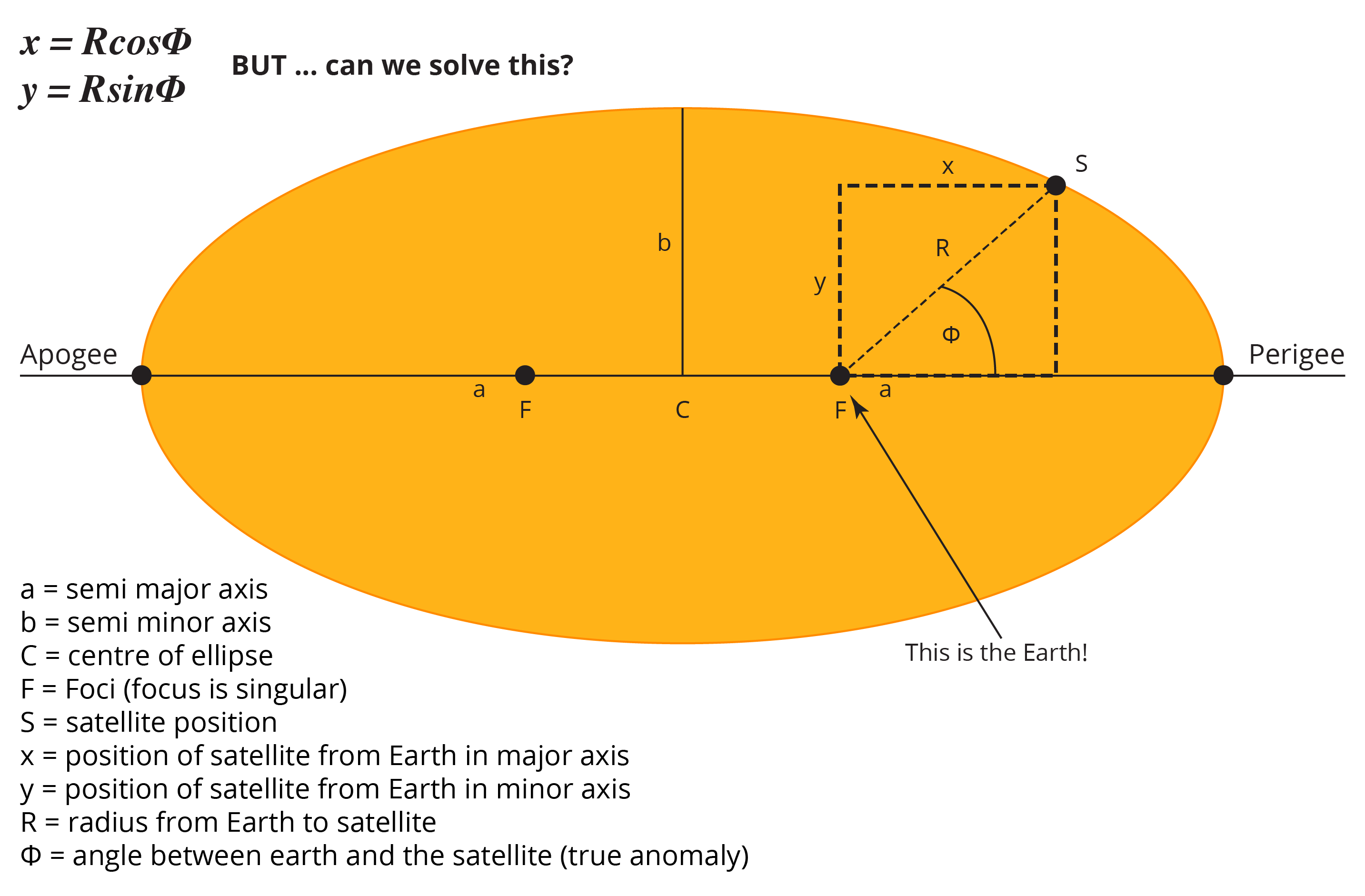
We can then use trigonometry to determine x the y values, however, doing the trigonometry on a shape that has a constant radius is significantly easier, so we project the position of the satellite onto a circle with a radius equal to the semi major axis, as shown in Figure 3.2(e). In the calculations on the circle, our x and y values become X and Y as shown.

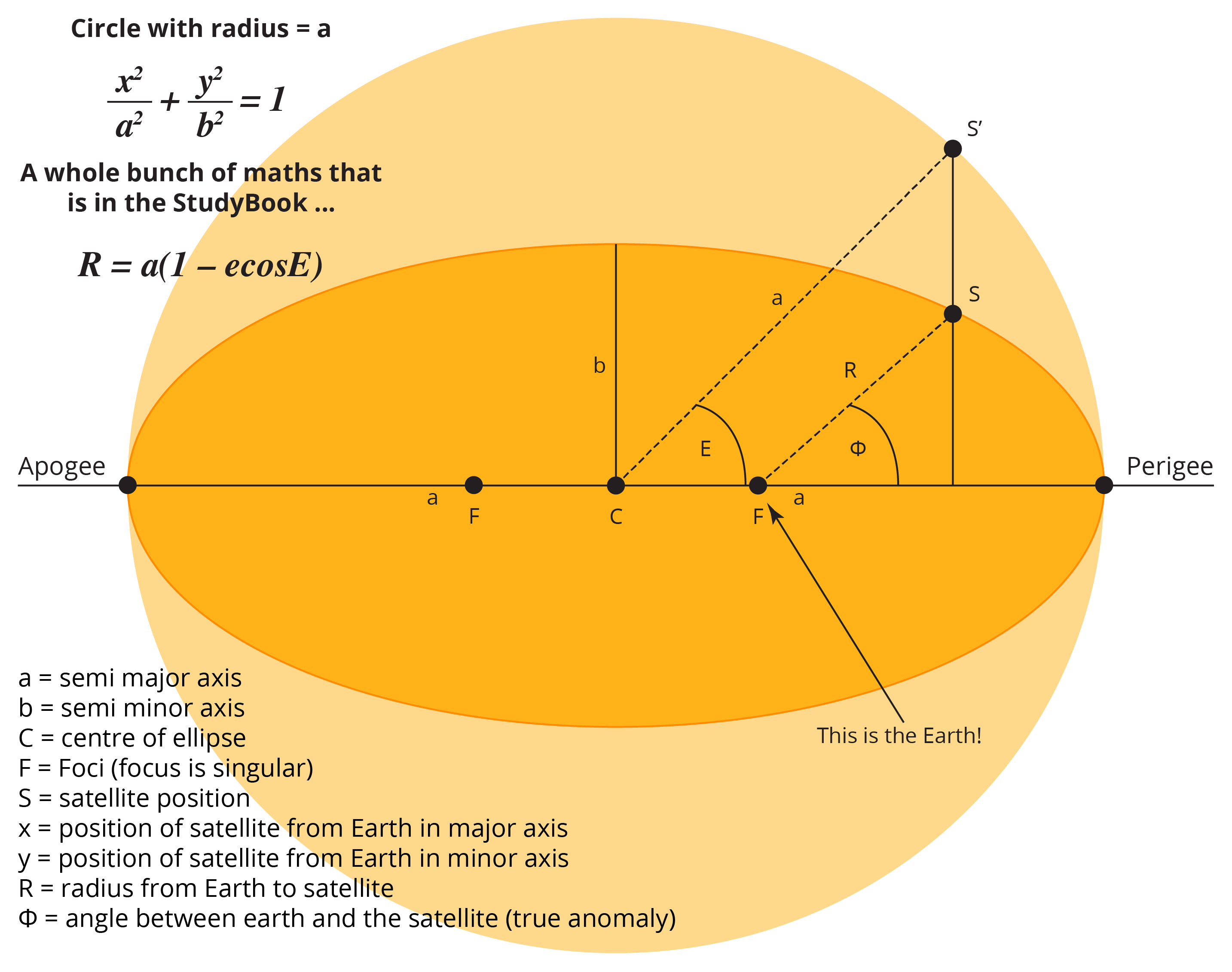
In astronomy, the angle between the satellite (or planet) given by , is called the true anomaly, while the angle between the centre of the ellipse and the satellite given by E is called the eccentric anomaly. These can be averaged to generate a mean anomaly, represented by M.

Considering the eccentricity of the ellipse and the mean anomaly, the version of Kepler’s first law that applies for GNSS satellites is:

It is worth noting that at the point where the satellite is at the perigee, there is more atmospheric friction compared with when the satellite is at the apogee. The orbit will tend to become more circular and closer to the earth until eventually the atmospheric friction becomes too large and burns up the satellite. This is important to know when we discuss the satellite orbit information, the ephemeris, later in this chapter.

Kepler’s second law – the Law of Areas

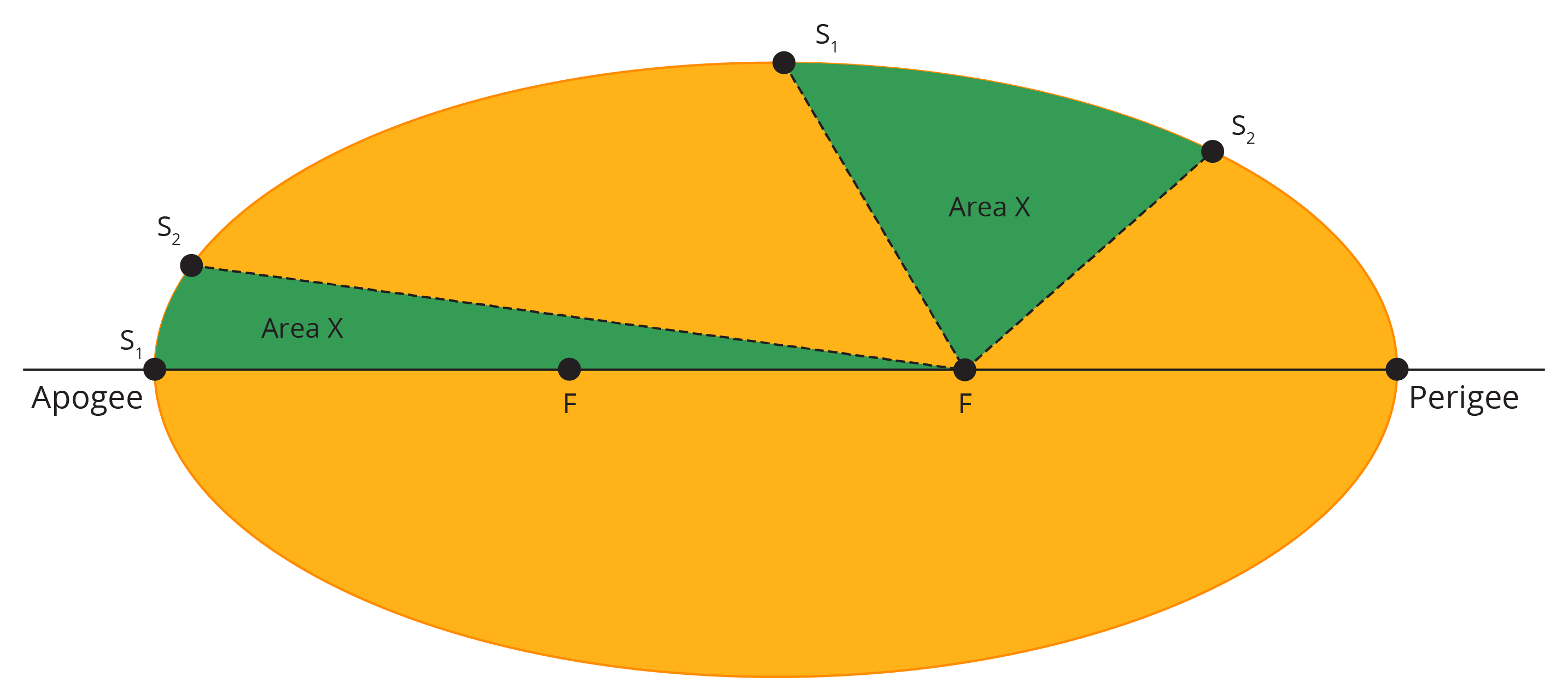
The second law is called the Law of Areas and showed that for a given time period a satellite will sweep out an equal area, regardless of where it is in its orbit. This in turn proved that the speed of a satellite changes at different points in its orbit, travelling faster when it is near the perigee, and slower near the apogee.

For satellites orbiting the Earth, this law is given by the equation:

In Figure 3.2(f) the time between S₁ and S₂ is the same for both sections of the orbit, and the area scribed out are also equal, despite the distance travelled by the satellite being different.

You can watch this YouTube clip on how the Law of Orbits works below.

Kepler’s third law – the Law of Periods