The system of Cartesian coordinates was developed by a French mathematician named René Descartes in the 17th century. A Cartesian coordinate system has three axes – X, Y & Z, which are in pairs perpendicular to each other, to represent the three dimensions.

A 3D Cartesian coordinate system must:

• share a common point, called the origin
• have an orientation for each axis
• use the same unit of length, for example, metres or kilometres.

The requirements for a Cartesian coordinate system are not that different to a datum, so using it as a coordinate system for the Earth becomes reasonably simple.

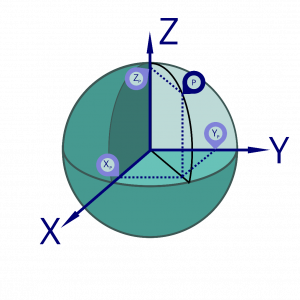
An Earth centred Earth fixed (ECEF) system has its centre at the centre of mass of the Earth, and the orientation of the axes are aligned with the Earth’s natural axis system. An example of a point, shown by P, and it’s location in an ECEF Cartesian coordinate system is shown in Figure 2.4(a).

Generally, the following is true for an ECEF Cartesian coordinate system that relates to a geocentric global datum:

• The origin is at the centre of mass of the Earth.
• The X axis and Y axis are perpendicular to each other, and form a plane that is the same as the plane formed by the equator, (called the equatorial plane).
• The X axis is at the prime meridian of Greenwich at 0° longitude.
• The Z axis is perpendicular to the X & Y axes, and aligns with the N-S pole, or axis of rotation, of the Earth.
• The axes are fixed to the Earth’s motion, so the coordinates of points are not constantly changing, apart for tectonic plate movement. This is why it is called “Earth fixed”.

ECEF Cartesian coordinates are generally shown as a set like (X, Y, Z), where they are all in the same units.

Importantly, an ECEF Cartesian coordinate system does not need a defined datum to express the coordinates of a point, however, you do need to know the origin and orientation of the axes of the coordinate system itself.

ECEF Cartesian coordinate systems and GNSS surveying

In more traditional surveying approaches, the horizontal position of something was most often dealt with separately to its vertical position or height. When GNSS came along, which is inherently a three dimensional system, a broader view of how to survey things had to be taken.

We will discuss the different GNSS techniques in Modules 4-6, however, it’s worth pointing out that ECEF Cartesian coordinates are utilised in a GNSS survey technique where we have two or more GNSS receivers collecting data at once. We are able to compare the positions of the GNSS receivers to calculate the three dimensional differences between them, which is known as a baseline. A baseline is usually represented by the Greek letter delta (which is often used to show that a value is the difference between two things), followed by the axis letter, for example, .

Coordinate transformations

Often data is collected on one reference surface, and for one of many reasons, may need to be changed to another reference surface, or even from one type of coordinate system to another. The process that moves the coordinates of points from one surface or system to another is called a transformation.

A transformation can involve a number of factors, including an origin change, rotation and scale to name a few, and these factors are known as transformation parameters, describing how the transformation needs to occur.

A type of transformation where we ‘slide’ all the points a consistent distance and direction is called a translation, which is often referred to in surveying as a block shift.

Moving between GDA94 and GDA2020 required a coordinate transformation. The transformation parameters for new datums to old datums are usually published at the same time as the definition of the new datum.