Coordinate system

We learnt in the that if we want to measure a position with GNSS, we need to have an understanding of the datum that we’re using – this part of the module covers how we describe that position using a coordinate system.

Most people are familiar with coordinates from a topographic map, or even from their GPS navigation system in their car or smartphone; they are essentially a numerical way of describing the position of something relative to a datum or other reference surface.

However, there are some differences between coordinates on a round shape like the Earth and a flat map!

The relationship between a datum and the positions on it can be represented by three different types of coordinate systems relevant to geodesy;

• geographic coordinate systems: Latitude, longitude and ellipsoidal heights
• earth centred Earth fixed (ECEF) Cartesian coordinates
• projection coordinates.

Geographic coordinate systems

Lines of latitude and longitude are a familiar sight to anyone who’s ever looked at a globe of the Earth, and they’re a concept that has been around for a long time.

Our ability to use them effectively is less recent though. While latitude is relatively easy to understand and use for navigation due to the equator and shadows (remember the well?!), longitude is a more tricky concept, particularly when navigating across vast oceans. An incredible amount of very smart people tried to solve the problem of longitude as far back at the 1400s. Eventually it was an English clockmaker named John Harrison who invented a device called the marine chronometer that proved to be the key piece in solving the problem. But back to coordinate systems…

A geographic coordinate system is used to define locations on the earth’s surface in three dimensions. The coordinates comprise angular measures (latitudes and longitudes) and heights referenced to a defined ellipsoidal datum surface.

Latitude, Longitude and ellipsoidal height are all dependent on the size, shape and position of the reference ellipsoid being used. This means that a position of a point described by a latitude, longitude and ellipsoidal height in one datum, say WGS84, will have a different latitude, longitude and ellipsoidal height on a different datum, like GDA2020. This is important to remember when measuring anything using GNSS!

Latitude and longitude are known as curvilinear coordinates, meaning they are expressed in angular units such as degrees, minutes and seconds of arc.

Latitude

A position’s latitude is measured relative to the equator – points in the southern hemisphere of the Earth will have a negative latitude value, while points in the northern hemisphere have a positive latitude value. At the equator latitude has a value of 0°, and at the poles is has a value of ±90°. Latitude is described by the lowercase Greek letter phi .

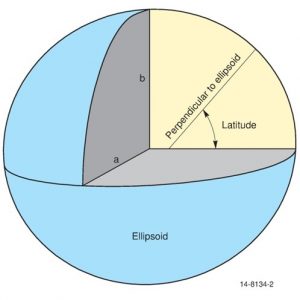
Technically, latitude is defined as the angle between the major axis of the ellipsoid and the normal to the tangent plane at that point, measured at the point of intersection of the normal with the equatorial plane. In more simple terms, latitude is essentially measuring the angle from the equator to the position of the point you are trying to measure. Figure 2.3(a) shows the semi major axis a, semi minor axis b, and the angle of latitude. Note the perpendicular to the ellipsoid line (also known as the normal) doesn’t intersect at the origin due to the ellipsoidal shape.

Lines of constant latitude are called parallels of latitude, as they are parallel to each other. These parallels are circles of different radius, where all the points on them are at the same angle from the equator.

Latitudes in Australia range from about -10° or 10° South (i.e. south of the equator) to about 45° South; and in mainland New Zealand from about 36° South to about 47° South.

Longitude

Longitude is the method we use to measure positions on a spheroid or ellipsoid in what is the East and West direction on the Earth. It is described using the lowercase Greek letter Lambda –

The lines of longitude are also called meridians of longitude, meaning that they all run from pole to pole – they’re the ones that look like segments of an orange. These meridians are all the same size and shape, and are also known as great ellipses if they have the same centre as the ellipsoid used in their datum.

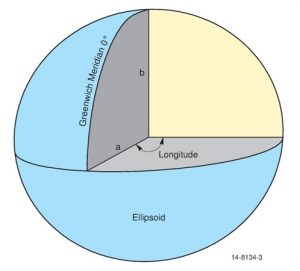
Longitude is described relative to the Royal Observatory in Greenwich England (pronounced Gren-itch) which is the meridian of 0°, making it the Prime Meridian. The other meridians are measured relative to the Prime Meridian along the equator. To the west of Greenwich the meridians are considered negative, through to -180°, while to the East they’re considered positive through to +180°. Figure 2.3(b) shows the angle of longitude relative to the Greenwich Meridian of 0°.

Longitudes in Australia range from about 110° East to about 155° East, and in New Zealand from about 167° East to 179° East, relative to the Greenwich Prime Meridian.

Distances from latitude and longitude

The distances subtended by one unit of measure (say one minute of arc) in latitude and longitude are not equal. For example, this means that the distance on the ellipsoid between latitudes of 10°13’ and 10°14’ (one minute of arc) won’t be equal to the distance on the ellipsoid between the longitudes of 10°13’ and 10°14’. At the equator the distance represented by one minute of latitude and one minute of longitude are approximately equal. This is because the equator is the only parallel of latitude whose radius is approximately equal to that of the meridians.

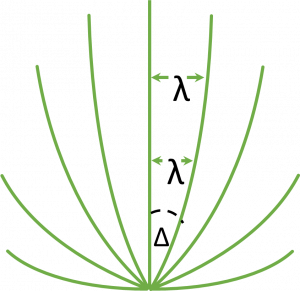
As the longitude meridians get closer together towards the poles (called converging) the distance between the meridians decreases. This is known as the meridian convergence, and is represented by the lowercase Greek letters delta and alpha – . Meridian convergence is shown in Figure 2.3(c).

Ellipsoidal heights

The third component of a geographic coordinate system is the ellipsoidal height, represented by lowercase (h). As covered in the section on ellipsoids and datums, ellipsoidal height is the difference between a point on the topography and the ellipsoid, which can be measured using GNSS, or calculated if you know the orthometric height (H) and the N value for the geoid-ellipsoidal separation.

Ellipsoidal height is measured along the ellipsoidal normal, from the surface of the ellipsoid to the point on the surface. The point on the ellipsoid is generally represented by while the point on the surface is represented by . Refer to the diagrams in the Datum chapter.