2 Thinking like a researcher

Conducting good research requires first retraining your brain to think like a researcher. This requires visualising the abstract from actual observations, mentally ‘connecting the dots’ to identify hidden concepts and patterns, and synthesising those patterns into generalisable laws and theories that apply to other contexts beyond the domain of the initial observations. Research involves constantly moving back and forth from an empirical plane where observations are conducted to a theoretical plane where these observations are abstracted into generalizable laws and theories. This is a skill that takes many years to develop, is not something that is taught in postgraduate or doctoral programs or acquired in industry training, and is by far the biggest deficit amongst PhD students. Some of the mental abstractions needed to think like a researcher include unit of analysis, constructs, hypotheses, operationalisation, theories, models, induction, deduction, and so forth, which we will examine in this chapter.

Unit of analysis

One of the first decisions in any social science research is the unit of analysis of a scientific study. The unit of analysis refers to the person, collective, or object that is the target of the investigation. Typical units of analysis include individuals, groups, organisations, countries, technologies, objects, and such. For instance, if we are interested in studying people’s shopping behaviour, their learning outcomes, or their attitudes to new technologies, then the unit of analysis is the individual. If we want to study characteristics of street gangs or teamwork in organisations, then the unit of analysis is the group. If the goal of research is to understand how firms can improve profitability or make good executive decisions, then the unit of analysis is the firm. In this case, even though decisions are made by individuals in these firms, these individuals are presumed to represent their firm’s decision rather than their personal decisions. If research is directed at understanding differences in national cultures, then the unit of analysis becomes a country. Even inanimate objects can serve as units of analysis. For instance, if a researcher is interested in understanding how to make web pages more attractive to users, then the unit of analysis is a web page rather than users. If we wish to study how knowledge transfer occurs between two firms, then our unit of analysis becomes the dyad—the combination of firms that is sending and receiving knowledge.

Understanding the units of analysis can sometimes be fairly complex. For instance, if we wish to study why certain neighbourhoods have high crime rates, then our unit of analysis becomes the neighbourhood, and not crimes or criminals committing such crimes. This is because the object of our inquiry is the neighbourhood and not criminals. However, if we wish to compare different types of crimes in different neighbourhoods, such as homicide, robbery, assault, and so forth, our unit of analysis becomes the crime. If we wish to study why criminals engage in illegal activities, then the unit of analysis becomes the individual (i.e., the criminal). Likewise, if we want to study why some innovations are more successful than others, then our unit of analysis is an innovation. However, if we wish to study how some organisations innovate more consistently than others, then the unit of analysis is the organisation. Hence, two related research questions within the same research study may have two entirely different units of analysis.

Understanding the unit of analysis is important because it shapes what type of data you should collect for your study and who you collect it from. If your unit of analysis is a web page, you should be collecting data about web pages from actual web pages, and not surveying people about how they use web pages. If your unit of analysis is the organisation, then you should be measuring organisational-level variables such as organisational size, revenues, hierarchy, or absorptive capacity. This data may come from a variety of sources such as financial records or surveys of Chief Executive Officers (CEO), who are presumed to be representing their organisation rather than themselves. Some variables such as CEO pay may seem like individual level variables, but in fact, it can also be an organisational level variable because each organisation has only one CEO to pay at any time. Sometimes, it is possible to collect data from a lower level of analysis and aggregate that data to a higher level of analysis. For instance, in order to study teamwork in organisations, you can survey individual team members in different organisational teams, and average their individual scores to create a composite team-level score for team-level variables like cohesion and conflict. We will examine the notion of ‘variables’ in greater depth in the next section.

Concepts, constructs, and variables

We discussed in Chapter 1 that although research can be exploratory, descriptive, or explanatory, most scientific research tends to be of the explanatory type in that it searches for potential explanations for observed natural or social phenomena. Explanations require development of concepts or generalisable properties or characteristics associated with objects, events, or people. While objects such as a person, a firm, or a car are not concepts, their specific characteristics or behaviour such as a person’s attitude toward immigrants, a firm’s capacity for innovation, and a car’s weight can be viewed as concepts.

Knowingly or unknowingly, we use different kinds of concepts in our everyday conversations. Some of these concepts have been developed over time through our shared language. Sometimes, we borrow concepts from other disciplines or languages to explain a phenomenon of interest. For instance, the idea of gravitation borrowed from physics can be used in business to describe why people tend to ‘gravitate’ to their preferred shopping destinations. Likewise, the concept of distance can be used to explain the degree of social separation between two otherwise collocated individuals. Sometimes, we create our own concepts to describe a unique characteristic not described in prior research. For instance, technostress is a new concept referring to the mental stress one may face when asked to learn a new technology.

Concepts may also have progressive levels of abstraction. Some concepts such as a person’s weight are precise and objective, while other concepts such as a person’s personality may be more abstract and difficult to visualise. A construct is an abstract concept that is specifically chosen (or ‘created’) to explain a given phenomenon. A construct may be a simple concept, such as a person’s weight, or a combination of a set of related concepts such as a person’s communication skill, which may consist of several underlying concepts such as the person’s vocabulary, syntax, and spelling. The former instance (weight) is a unidimensional construct, while the latter (communication skill) is a multidimensional construct (i.e., it consists of multiple underlying concepts). The distinctions between constructs and concepts are clearer in multi-dimensional constructs, where the higher order abstraction is called a construct and the lower order abstractions are called concepts. However, this distinction tends to blur in the case of unidimensional constructs.

Constructs used for scientific research must have precise and clear definitions that others can use to understand exactly what it means and what it does not mean. For instance, a seemingly simple construct such as income may refer to monthly or annual income, before-tax or after-tax income, and personal or family income, and is therefore neither precise nor clear. There are two types of definitions: dictionary definitions and operational definitions. In the more familiar dictionary definition, a construct is often defined in terms of a synonym. For instance, attitude may be defined as a disposition, a feeling, or an affect, and affect in turn is defined as an attitude. Such definitions of a circular nature are not particularly useful in scientific research for elaborating the meaning and content of that construct. Scientific research requires operational definitions that define constructs in terms of how they will be empirically measured. For instance, the operational definition of a construct such as temperature must specify whether we plan to measure temperature in Celsius, Fahrenheit, or Kelvin scale. A construct such as income should be defined in terms of whether we are interested in monthly or annual income, before-tax or after-tax income, and personal or family income. One can imagine that constructs such as learning, personality, and intelligence can be quite hard to define operationally.

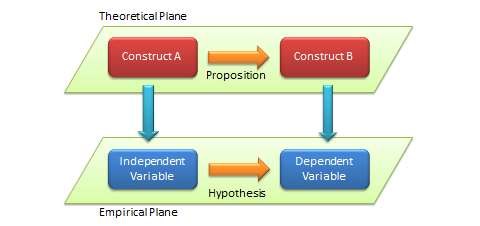
A term frequently associated with, and sometimes used interchangeably with, a construct is a variable. Etymologically speaking, a variable is a quantity that can vary (e.g., from low to high, negative to positive, etc.), in contrast to constants that do not vary (i.e., remain constant). However, in scientific research, a variable is a measurable representation of an abstract construct. As abstract entities, constructs are not directly measurable, and hence, we look for proxy measures called variables. For instance, a person’s intelligence is often measured as his or her IQ (intelligence quotient) score, which is an index generated from an analytical and pattern-matching test administered to people. In this case, intelligence is a construct, and IQ score is a variable that measures the intelligence construct. Whether IQ scores truly measure one’s intelligence is anyone’s guess (though many believe that they do), and depending on whether or how well it measures intelligence, the IQ score may be a good or a poor measure of the intelligence construct. As shown in Figure 2.1, scientific research proceeds along two planes: a theoretical plane and an empirical plane. Constructs are conceptualised at the theoretical (abstract) plane, while variables are operationalised and measured at the empirical (observational) plane. Thinking like a researcher implies the ability to move back and forth between these two planes.

Depending on their intended use, variables may be classified as independent, dependent, moderating, mediating, or control variables. Variables that explain other variables are called independent variables, those that are explained by other variables are dependent variables, those that are explained by independent variables while also explaining dependent variables are mediating variables (or intermediate variables), and those that influence the relationship between independent and dependent variables are called moderating variables. As an example, if we state that higher intelligence causes improved learning among students, then intelligence is an independent variable and learning is a dependent variable. There may be other extraneous variables that are not pertinent to explaining a given dependent variable, but may have some impact on the dependent variable. These variables must be controlled in a scientific study, and are therefore called control variables.

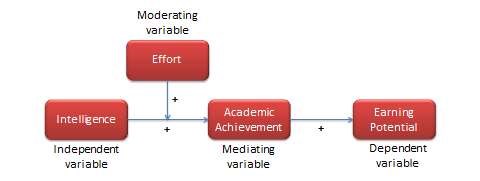
To understand the differences between these different variable types, consider the example shown in Figure 2.2. If we believe that intelligence influences (or explains) students’ academic achievement, then a measure of intelligence such as an IQ score is an independent variable, while a measure of academic success such as a GPA (grade point average) is a dependent variable. If we believe that the effect of intelligence on academic achievement also depends on the effort invested by the student in the learning process (i.e., between two equally intelligent students, the student who puts in more effort achieves higher academic achievement than one who puts in less effort), then effort becomes a moderating variable. Incidentally, one may also view effort as an independent variable and intelligence as a moderating variable. If academic achievement is viewed as an intermediate step to higher earning potential, then earning potential becomes the dependent variable for the independent variable academic achievement, and academic achievement becomes the mediating variable in the relationship between intelligence and earning potential. Hence, variables are defined as an independent, dependent, moderating, or mediating variable based on their nature of association with each other. The overall network of relationships between a set of related constructs is called a nomological network (see Figure 2.2). Thinking like a researcher requires not only being able to abstract constructs from observations, but also being able to mentally visualise a nomological network linking these abstract constructs.

Propositions and hypotheses

Figure 2.2 shows how theoretical constructs such as intelligence, effort, academic achievement, and earning potential are related to each other in a nomological network. Each of these relationships is called a proposition. In seeking explanations to a given phenomenon or behaviour, it is not adequate just to identify key concepts and constructs underlying the target phenomenon or behaviour. We must also identify and state patterns of relationships between these constructs. Such patterns of relationships are called propositions. A proposition is a tentative and conjectural relationship between constructs that is stated in a declarative form. An example of a proposition is: ‘An increase in student intelligence causes an increase in their academic achievement’. This declarative statement does not have to be true, but must be empirically testable using data, so that we can judge whether it is true or false. Propositions are generally derived based on logic (deduction) or empirical observations (induction).

Because propositions are associations between abstract constructs, they cannot be tested directly. Instead, they are tested indirectly by examining the relationship between corresponding measures (variables) of those constructs. The empirical formulations of propositions, stated as relationships between variables, are called hypotheses (see Figure 2.1). Since IQ scores and GPAs are operational measures of intelligence and academic achievement respectively, the above proposition can be specified in form of the hypothesis: ‘An increase in students’ IQ score causes an increase in their GPA’. Propositions are specified in the theoretical plane, while hypotheses are specified in the empirical plane. Hence, hypotheses are empirically testable using observed data, and may be rejected if not supported by empirical observations. Of course, the goal of hypothesis testing is to infer whether the corresponding proposition is valid.

Hypotheses can be strong or weak. ‘Students’ IQ scores are related to their academic achievement’ is an example of a weak hypothesis, since it indicates neither the directionality of the hypothesis (i.e., whether the relationship is positive or negative), nor its causality (i.e., whether intelligence causes academic achievement or academic achievement causes intelligence). A stronger hypothesis is ‘students’ IQ scores are positively related to their academic achievement’, which indicates the directionality but not the causality. A still better hypothesis is ‘students’ IQ scores have positive effects on their academic achievement’, which specifies both the directionality and the causality (i.e., intelligence causes academic achievement, and not the reverse). The signs in Figure 2.2 indicate the directionality of the respective hypotheses.

Also note that scientific hypotheses should clearly specify independent and dependent variables. In the hypothesis, ‘students’ IQ scores have positive effects on their academic achievement’, it is clear that intelligence is the independent variable (the ‘cause’) and academic achievement is the dependent variable (the ‘effect’). Further, it is also clear that this hypothesis can be evaluated as either true (if higher intelligence leads to higher academic achievement) or false (if higher intelligence has no effect on or leads to lower academic achievement). Later on in this book, we will examine how to empirically test such cause-effect relationships. Statements such as ‘students are generally intelligent’ or ‘all students can achieve academic success’ are not scientific hypotheses because they do not specify independent and dependent variables, nor do they specify a directional relationship that can be evaluated as true or false.

Theories and models

A theory is a set of systematically interrelated constructs and propositions intended to explain and predict a phenomenon or behaviour of interest, within certain boundary conditions and assumptions. Essentially, a theory is a systemic collection of related theoretical propositions. While propositions generally connect two or three constructs, theories represent a system of multiple constructs and propositions. Hence, theories can be substantially more complex and abstract and of a larger scope than propositions or hypotheses.

I must note here that people unfamiliar with scientific research often view a theory as a speculation or the opposite of fact. For instance, people often say that teachers need to be less theoretical and more practical or factual in their classroom teaching. However, practice or fact are not opposites of theory, but in a scientific sense, are essential components needed to test the validity of a theory. A good scientific theory should be well supported using observed facts and should also have practical value, while a poorly defined theory tends to be lacking in these dimensions. Famous organisational researcher Kurt Lewin once said, ‘Theory without practice is sterile; practice without theory is blind’. Hence, both theory and facts (or practice) are essential for scientific research.

Theories provide explanations of social or natural phenomenon. As emphasised in Chapter 1, these explanations may be good or poor. Hence, there may be good or poor theories. Chapter 3 describes some criteria that can be used to evaluate how good a theory really is. Nevertheless, it is important for researchers to understand that theory is not ‘truth’, there is nothing sacrosanct about any theory, and theories should not be accepted just because they were proposed by someone. In the course of scientific progress, poorer theories are eventually replaced by better theories with higher explanatory power. The essential challenge for researchers is to build better and more comprehensive theories that can explain a target phenomenon better than prior theories.

A term often used in conjunction with theory is a model. A model is a representation of all or part of a system that is constructed to study that system (e.g., how the system works or what triggers the system). While a theory tries to explain a phenomenon, a model tries to represent a phenomenon. Models are often used by decision makers to make important decisions based on a given set of inputs. For instance, marketing managers may use models to decide how much money to spend on advertising for different product lines based on parameters such as prior year’s advertising expenses, sales, market growth, and competing products. Likewise, weather forecasters can use models to predict future weather patterns based on parameters such as wind speeds, wind direction, temperature, and humidity. While these models are useful, they may not necessarily explain advertising expenditure or weather forecasts. Models may be of different kinds, such as mathematical models, network models, and path models. Models can also be descriptive, predictive, or normative. Descriptive models are frequently used for representing complex systems, and for visualising variables and relationships in such systems. An advertising expenditure model may be a descriptive model. Predictive models (e.g., a regression model) allow forecast of future events. Weather forecasting models are predictive models. Normative models are used to guide our activities along commonly accepted norms or practices. Models may also be static if they represent the state of a system at one point in time, or dynamic, if they represent a system’s evolution over time.

The process of theory or model development may involve inductive and deductive reasoning. Recall from Chapter 1 that deduction is the process of drawing conclusions about a phenomenon or behaviour based on theoretical or logical reasons and an initial set of premises. As an example, if a certain bank enforces a strict code of ethics for its employees (Premise 1), and Jamie is an employee at that bank (Premise 2), then Jamie can be trusted to follow ethical practices (Conclusion). In deduction, the conclusions must be true if the initial premises and reasons are correct.

In contrast, induction is the process of drawing conclusions based on facts or observed evidence. For instance, if a firm spent a lot of money on a promotional campaign (Observation 1), but the sales did not increase (Observation 2), then possibly the promotion campaign was poorly executed (Conclusion). However, there may be rival explanations for poor sales, such as economic recession or the emergence of a competing product or brand or perhaps a supply chain problem. Inductive conclusions are therefore only a hypothesis, and may be disproven. Deductive conclusions generally tend to be stronger than inductive conclusions, but a deductive conclusion based on an incorrect premise is also incorrect.

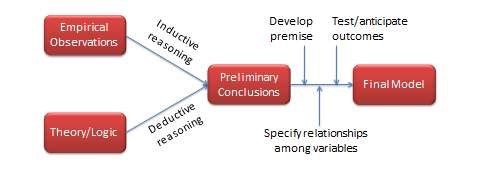
As shown in Figure 2.3, inductive and deductive reasoning go hand in hand in theory and model building. Induction occurs when we observe a fact and ask, ‘Why is this happening?’. In answering this question, we advance one or more tentative explanations (hypotheses). We then use deduction to narrow down the tentative explanations to the most plausible explanation based on logic and reasonable premises (based on our understanding of the phenomenon under study). Researchers must be able to move back and forth between inductive and deductive reasoning if they are to post extensions or modifications to a given model or theory, or build better ones, both of which are the essence of scientific research.