10 Experimental research
Experimental research—often considered to be the ‘gold standard’ in research designs—is one of the most rigorous of all research designs. In this design, one or more independent variables are manipulated by the researcher (as treatments), subjects are randomly assigned to different treatment levels (random assignment), and the results of the treatments on outcomes (dependent variables) are observed. The unique strength of experimental research is its internal validity (causality) due to its ability to link cause and effect through treatment manipulation, while controlling for the spurious effect of extraneous variable.
Experimental research is best suited for explanatory research—rather than for descriptive or exploratory research—where the goal of the study is to examine cause-effect relationships. It also works well for research that involves a relatively limited and well-defined set of independent variables that can either be manipulated or controlled. Experimental research can be conducted in laboratory or field settings. Laboratory experiments, conducted in laboratory (artificial) settings, tend to be high in internal validity, but this comes at the cost of low external validity (generalisability), because the artificial (laboratory) setting in which the study is conducted may not reflect the real world. Field experiments are conducted in field settings such as in a real organisation, and are high in both internal and external validity. But such experiments are relatively rare, because of the difficulties associated with manipulating treatments and controlling for extraneous effects in a field setting.
Experimental research can be grouped into two broad categories: true experimental designs and quasi-experimental designs. Both designs require treatment manipulation, but while true experiments also require random assignment, quasi-experiments do not. Sometimes, we also refer to non-experimental research, which is not really a research design, but an all-inclusive term that includes all types of research that do not employ treatment manipulation or random assignment, such as survey research, observational research, and correlational studies.
Basic concepts
Treatment and control groups. In experimental research, some subjects are administered one or more experimental stimulus called a treatment (the treatment group) while other subjects are not given such a stimulus (the control group). The treatment may be considered successful if subjects in the treatment group rate more favourably on outcome variables than control group subjects. Multiple levels of experimental stimulus may be administered, in which case, there may be more than one treatment group. For example, in order to test the effects of a new drug intended to treat a certain medical condition like dementia, if a sample of dementia patients is randomly divided into three groups, with the first group receiving a high dosage of the drug, the second group receiving a low dosage, and the third group receiving a placebo such as a sugar pill (control group), then the first two groups are experimental groups and the third group is a control group. After administering the drug for a period of time, if the condition of the experimental group subjects improved significantly more than the control group subjects, we can say that the drug is effective. We can also compare the conditions of the high and low dosage experimental groups to determine if the high dose is more effective than the low dose.
Treatment manipulation. Treatments are the unique feature of experimental research that sets this design apart from all other research methods. Treatment manipulation helps control for the ‘cause’ in cause-effect relationships. Naturally, the validity of experimental research depends on how well the treatment was manipulated. Treatment manipulation must be checked using pretests and pilot tests prior to the experimental study. Any measurements conducted before the treatment is administered are called pretest measures, while those conducted after the treatment are posttest measures.
Random selection and assignment. Random selection is the process of randomly drawing a sample from a population or a sampling frame. This approach is typically employed in survey research, and ensures that each unit in the population has a positive chance of being selected into the sample. Random assignment, however, is a process of randomly assigning subjects to experimental or control groups. This is a standard practice in true experimental research to ensure that treatment groups are similar (equivalent) to each other and to the control group prior to treatment administration. Random selection is related to sampling, and is therefore more closely related to the external validity (generalisability) of findings. However, random assignment is related to design, and is therefore most related to internal validity. It is possible to have both random selection and random assignment in well-designed experimental research, but quasi-experimental research involves neither random selection nor random assignment.
Threats to internal validity. Although experimental designs are considered more rigorous than other research methods in terms of the internal validity of their inferences (by virtue of their ability to control causes through treatment manipulation), they are not immune to internal validity threats. Some of these threats to internal validity are described below, within the context of a study of the impact of a special remedial math tutoring program for improving the math abilities of high school students.
History threat is the possibility that the observed effects (dependent variables) are caused by extraneous or historical events rather than by the experimental treatment. For instance, students’ post-remedial math score improvement may have been caused by their preparation for a math exam at their school, rather than the remedial math program.
Maturation threat refers to the possibility that observed effects are caused by natural maturation of subjects (e.g., a general improvement in their intellectual ability to understand complex concepts) rather than the experimental treatment.
Testing threat is a threat in pre-post designs where subjects’ posttest responses are conditioned by their pretest responses. For instance, if students remember their answers from the pretest evaluation, they may tend to repeat them in the posttest exam.
Not conducting a pretest can help avoid this threat.
Instrumentation threat, which also occurs in pre-post designs, refers to the possibility that the difference between pretest and posttest scores is not due to the remedial math program, but due to changes in the administered test, such as the posttest having a higher or lower degree of difficulty than the pretest.
Mortality threat refers to the possibility that subjects may be dropping out of the study at differential rates between the treatment and control groups due to a systematic reason, such that the dropouts were mostly students who scored low on the pretest. If the low-performing students drop out, the results of the posttest will be artificially inflated by the preponderance of high-performing students.
Regression threat—also called a regression to the mean—refers to the statistical tendency of a group’s overall performance to regress toward the mean during a posttest rather than in the anticipated direction. For instance, if subjects scored high on a pretest, they will have a tendency to score lower on the posttest (closer to the mean) because their high scores (away from the mean) during the pretest were possibly a statistical aberration. This problem tends to be more prevalent in non-random samples and when the two measures are imperfectly correlated.
Two-group experimental designs
The simplest true experimental designs are two group designs involving one treatment group and one control group. These are ideally suited for testing the effects of a single independent variable that can be manipulated as a treatment. The two basic two-group designs are the pretest-posttest control group design and the posttest-only control group design, while variations may include covariance designs. These designs are often depicted using a standardised design notation, where ![]() represents random assignment of subjects to groups,
represents random assignment of subjects to groups, ![]() represents the treatment administered to the treatment group, and
represents the treatment administered to the treatment group, and ![]() represents pretest or posttest observations of the dependent variable (with different subscripts to distinguish between pretest and posttest observations of treatment and control groups).
represents pretest or posttest observations of the dependent variable (with different subscripts to distinguish between pretest and posttest observations of treatment and control groups).
Pretest-posttest control group design. In this design, subjects are randomly assigned to treatment and control groups, subjected to an initial (pretest) measurement of the dependent variables of interest, the treatment group is administered a treatment (representing the independent variable of interest), and the dependent variables measured again (posttest). The notation of this design is shown in Figure 10.1.

The effect ![]() of the experimental treatment in the pretest-posttest design is measured as the difference in the posttest and pretest scores between the treatment and control groups:
of the experimental treatment in the pretest-posttest design is measured as the difference in the posttest and pretest scores between the treatment and control groups:
![]()
Statistical analysis of this design involves a simple analysis of variance (ANOVA) between the treatment and control groups. The pretest-posttest design handles several threats to internal validity, such as maturation, testing, and regression, since these threats can be expected to influence both treatment and control groups in a similar (random) manner. The selection threat is controlled via random assignment. However, additional threats to internal validity may exist. For instance, mortality can be a problem if there are differential dropout rates between the two groups, and the pretest measurement may bias the posttest measurement—especially if the pretest introduces unusual topics or content.
Posttest-only control group design. This design is a simpler version of the pretest-posttest design where pretest measurements are omitted. The design notation is shown in Figure 10.2.

The treatment effect is measured simply as the difference in the posttest scores between the two groups:
![]()
The appropriate statistical analysis of this design is also a two-group analysis of variance (ANOVA). The simplicity of this design makes it more attractive than the pretest-posttest design in terms of internal validity. This design controls for maturation, testing, regression, selection, and pretest-posttest interaction, though the mortality threat may continue to exist.
Covariance designs. Sometimes, measures of dependent variables may be influenced by extraneous variables called covariates. Covariates are those variables that are not of central interest to an experimental study, but should nevertheless be controlled in an experimental design in order to eliminate their potential effect on the dependent variable and therefore allow for a more accurate detection of the effects of the independent variables of interest. The experimental designs discussed earlier did not control for such covariates. A covariance design —also called a concomitant variable design—is a special type of pretest-posttest control group design where the pretest measure is essentially a measurement of the covariates of interest rather than that of the dependent variables. The design notation is shown in Figure 10.3, where ![]() represents the covariates.
represents the covariates.

Because the pretest measure is not a measurement of the dependent variable, but rather a covariate, the treatment effect is measured as the difference in the posttest scores between the treatment and control groups as:
![]()
Due to the presence of covariates, the right statistical analysis of this design is a two-group analysis of covariance (ANCOVA). This design has all the advantages of posttest-only design, but with internal validity due to the controlling of covariates. Covariance designs can also be extended to pretest-posttest control group design.
Factorial designs
Two-group designs are inadequate if your research requires manipulation of two or more independent variables (treatments). In such cases, you would need four or higher-group designs. Such designs, quite popular in experimental research, are commonly called factorial designs. Each independent variable in this design is called a factor, and each subdivision of a factor is called a level. Factorial designs enable the researcher to examine not only the individual effect of each treatment on the dependent variables (called main effects), but also their joint effect (called interaction effects).
The most basic factorial design is a ![]() factorial design, which consists of two treatments, each with two levels (such as high/low or present/absent). For instance, say that you want to compare the learning outcomes of two different types of instructional techniques (in-class and online instruction), and you also want to examine whether these effects vary with the time of instruction (one and a half or three hours per week). In this case, you have two factors: instructional type and instructional time, each with two levels (in-class and online for instructional type, and one and a half and three hours/week for instructional time), as shown in Figure 8.1. If you wish to add a third level of instructional time (say six hours/week), then the second factor will consist of three levels and you will have a
factorial design, which consists of two treatments, each with two levels (such as high/low or present/absent). For instance, say that you want to compare the learning outcomes of two different types of instructional techniques (in-class and online instruction), and you also want to examine whether these effects vary with the time of instruction (one and a half or three hours per week). In this case, you have two factors: instructional type and instructional time, each with two levels (in-class and online for instructional type, and one and a half and three hours/week for instructional time), as shown in Figure 8.1. If you wish to add a third level of instructional time (say six hours/week), then the second factor will consist of three levels and you will have a ![]() factorial design. On the other hand, if you wish to add a third factor such as group work (present versus absent), you will have a
factorial design. On the other hand, if you wish to add a third factor such as group work (present versus absent), you will have a ![]() factorial design. In this notation, each number represents a factor, and the value of each factor represents the number of levels in that factor.
factorial design. In this notation, each number represents a factor, and the value of each factor represents the number of levels in that factor.
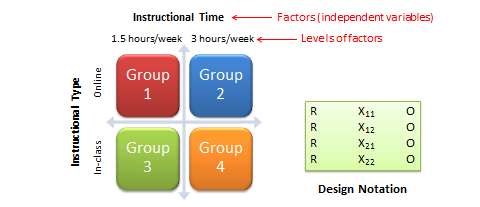
Factorial designs can also be depicted using a design notation, such as that shown on the right panel of Figure 10.4. ![]() represents random assignment of subjects to treatment groups,
represents random assignment of subjects to treatment groups, ![]() represents the treatment groups themselves (the subscripts of
represents the treatment groups themselves (the subscripts of ![]() represent the level of each factor), and
represent the level of each factor), and ![]() represent observations of the dependent variable. Notice that the
represent observations of the dependent variable. Notice that the ![]() factorial design will have four treatment groups, corresponding to the four combinations of the two levels of each factor. Correspondingly, the
factorial design will have four treatment groups, corresponding to the four combinations of the two levels of each factor. Correspondingly, the ![]() design will have six treatment groups, and the
design will have six treatment groups, and the ![]() design will have eight treatment groups. As a rule of thumb, each cell in a factorial design should have a minimum sample size of 20 (this estimate is derived from Cohen’s power calculations based on medium effect sizes). So a
design will have eight treatment groups. As a rule of thumb, each cell in a factorial design should have a minimum sample size of 20 (this estimate is derived from Cohen’s power calculations based on medium effect sizes). So a ![]() factorial design requires a minimum total sample size of 160 subjects, with at least 20 subjects in each cell. As you can see, the cost of data collection can increase substantially with more levels or factors in your factorial design. Sometimes, due to resource constraints, some cells in such factorial designs may not receive any treatment at all. These are called incomplete factorial designs. Such incomplete designs hurt our ability to draw inferences about the incomplete factors.
factorial design requires a minimum total sample size of 160 subjects, with at least 20 subjects in each cell. As you can see, the cost of data collection can increase substantially with more levels or factors in your factorial design. Sometimes, due to resource constraints, some cells in such factorial designs may not receive any treatment at all. These are called incomplete factorial designs. Such incomplete designs hurt our ability to draw inferences about the incomplete factors.
In a factorial design, a main effect is said to exist if the dependent variable shows a significant difference between multiple levels of one factor, at all levels of other factors. No change in the dependent variable across factor levels is the null case (baseline), from which main effects are evaluated. In the above example, you may see a main effect of instructional type, instructional time, or both on learning outcomes. An interaction effect exists when the effect of differences in one factor depends upon the level of a second factor. In our example, if the effect of instructional type on learning outcomes is greater for three hours/week of instructional time than for one and a half hours/week, then we can say that there is an interaction effect between instructional type and instructional time on learning outcomes. Note that the presence of interaction effects dominate and make main effects irrelevant, and it is not meaningful to interpret main effects if interaction effects are significant.
Hybrid experimental designs
Hybrid designs are those that are formed by combining features of more established designs. Three such hybrid designs are randomised bocks design, Solomon four-group design, and switched replications design.
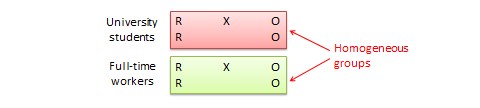
Randomised block design. This is a variation of the posttest-only or pretest-posttest control group design where the subject population can be grouped into relatively homogeneous subgroups (called blocks) within which the experiment is replicated. For instance, if you want to replicate the same posttest-only design among university students and full-time working professionals (two homogeneous blocks), subjects in both blocks are randomly split between the treatment group (receiving the same treatment) and the control group (see Figure 10.5). The purpose of this design is to reduce the ‘noise’ or variance in data that may be attributable to differences between the blocks so that the actual effect of interest can be detected more accurately.
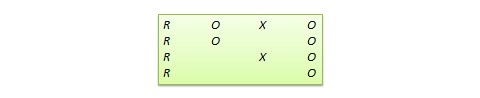
Solomon four-group design. In this design, the sample is divided into two treatment groups and two control groups. One treatment group and one control group receive the pretest, and the other two groups do not. This design represents a combination of posttest-only and pretest-posttest control group design, and is intended to test for the potential biasing effect of pretest measurement on posttest measures that tends to occur in pretest-posttest designs, but not in posttest-only designs. The design notation is shown in Figure 10.6.
Switched replication design. This is a two-group design implemented in two phases with three waves of measurement. The treatment group in the first phase serves as the control group in the second phase, and the control group in the first phase becomes the treatment group in the second phase, as illustrated in Figure 10.7. In other words, the original design is repeated or replicated temporally with treatment/control roles switched between the two groups. By the end of the study, all participants will have received the treatment either during the first or the second phase. This design is most feasible in organisational contexts where organisational programs (e.g., employee training) are implemented in a phased manner or are repeated at regular intervals.
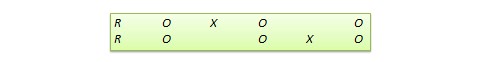
Quasi-experimental designs
Quasi-experimental designs are almost identical to true experimental designs, but lacking one key ingredient: random assignment. For instance, one entire class section or one organisation is used as the treatment group, while another section of the same class or a different organisation in the same industry is used as the control group. This lack of random assignment potentially results in groups that are non-equivalent, such as one group possessing greater mastery of certain content than the other group, say by virtue of having a better teacher in a previous semester, which introduces the possibility of selection bias. Quasi-experimental designs are therefore inferior to true experimental designs in interval validity due to the presence of a variety of selection related threats such as selection-maturation threat (the treatment and control groups maturing at different rates), selection-history threat (the treatment and control groups being differentially impacted by extraneous or historical events), selection-regression threat (the treatment and control groups regressing toward the mean between pretest and posttest at different rates), selection-instrumentation threat (the treatment and control groups responding differently to the measurement), selection-testing (the treatment and control groups responding differently to the pretest), and selection-mortality (the treatment and control groups demonstrating differential dropout rates). Given these selection threats, it is generally preferable to avoid quasi-experimental designs to the greatest extent possible.
Many true experimental designs can be converted to quasi-experimental designs by omitting random assignment. For instance, the quasi-equivalent version of pretest-posttest control group design is called non-equivalent groups design (NEGD), as shown in Figure 10.8, with random assignment ![]() replaced by non-equivalent (non-random) assignment
replaced by non-equivalent (non-random) assignment ![]() . Likewise, the quasi-experimental version of switched replication design is called non-equivalent switched replication design (see Figure 10.9).
. Likewise, the quasi-experimental version of switched replication design is called non-equivalent switched replication design (see Figure 10.9).
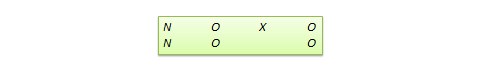

In addition, there are quite a few unique non-equivalent designs without corresponding true experimental design cousins. Some of the more useful of these designs are discussed next.
Regression discontinuity (RD) design. This is a non-equivalent pretest-posttest design where subjects are assigned to the treatment or control group based on a cut-off score on a preprogram measure. For instance, patients who are severely ill may be assigned to a treatment group to test the efficacy of a new drug or treatment protocol and those who are mildly ill are assigned to the control group. In another example, students who are lagging behind on standardised test scores may be selected for a remedial curriculum program intended to improve their performance, while those who score high on such tests are not selected from the remedial program.
The design notation can be represented as follows, where ![]() represents the cut-off score:
represents the cut-off score:
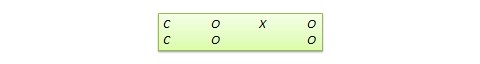
Because of the use of a cut-off score, it is possible that the observed results may be a function of the cut-off score rather than the treatment, which introduces a new threat to internal validity. However, using the cut-off score also ensures that limited or costly resources are distributed to people who need them the most, rather than randomly across a population, while simultaneously allowing a quasi-experimental treatment. The control group scores in the RD design do not serve as a benchmark for comparing treatment group scores, given the systematic non-equivalence between the two groups. Rather, if there is no discontinuity between pretest and posttest scores in the control group, but such a discontinuity persists in the treatment group, then this discontinuity is viewed as evidence of the treatment effect.
Proxy pretest design. This design, shown in Figure 10.11, looks very similar to the standard NEGD (pretest-posttest) design, with one critical difference: the pretest score is collected after the treatment is administered. A typical application of this design is when a researcher is brought in to test the efficacy of a program (e.g., an educational program) after the program has already started and pretest data is not available. Under such circumstances, the best option for the researcher is often to use a different prerecorded measure, such as students’ grade point average before the start of the program, as a proxy for pretest data. A variation of the proxy pretest design is to use subjects’ posttest recollection of pretest data, which may be subject to recall bias, but nevertheless may provide a measure of perceived gain or change in the dependent variable.
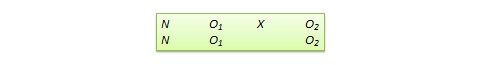
Separate pretest-posttest samples design. This design is useful if it is not possible to collect pretest and posttest data from the same subjects for some reason. As shown in Figure 10.12, there are four groups in this design, but two groups come from a single non-equivalent group, while the other two groups come from a different non-equivalent group. For instance, say you want to test customer satisfaction with a new online service that is implemented in one city but not in another. In this case, customers in the first city serve as the treatment group and those in the second city constitute the control group. If it is not possible to obtain pretest and posttest measures from the same customers, you can measure customer satisfaction at one point in time, implement the new service program, and measure customer satisfaction (with a different set of customers) after the program is implemented. Customer satisfaction is also measured in the control group at the same times as in the treatment group, but without the new program implementation. The design is not particularly strong, because you cannot examine the changes in any specific customer’s satisfaction score before and after the implementation, but you can only examine average customer satisfaction scores. Despite the lower internal validity, this design may still be a useful way of collecting quasi-experimental data when pretest and posttest data is not available from the same subjects.

Non-equivalent dependent variable (NEDV) design. This is a single-group pre-post quasi-experimental design with two outcome measures, where one measure is theoretically expected to be influenced by the treatment and the other measure is not. For instance, if you are designing a new calculus curriculum for high school students, this curriculum is likely to influence students’ posttest calculus scores, but not algebra scores. However, the posttest algebra scores may still vary due to extraneous factors such as history or maturation. Hence, the pre-post algebra scores can be treated as a control measure, while the pre-post calculus scores can be used as the treatment measure. The design notation, shown in Figure 10.13, indicates the single group by a single ![]() , followed by pretest
, followed by pretest ![]() and posttest
and posttest ![]() for calculus and algebra for the same group of students. This design is weak in internal validity, but its advantage lies in not having to use a separate control group.
for calculus and algebra for the same group of students. This design is weak in internal validity, but its advantage lies in not having to use a separate control group.
An interesting variation of the NEDV design is a pattern-matching NEDV design, which employs multiple outcome variables and a theory that explains how much each variable will be affected by the treatment. The researcher can then examine if the theoretical prediction is matched in actual observations. This pattern-matching technique—based on the degree of correspondence between theoretical and observed patterns—is a powerful way of alleviating internal validity concerns in the original NEDV design.
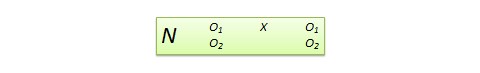
Perils of experimental research
Experimental research is one of the most difficult of research designs, and should not be taken lightly. This type of research is often best with a multitude of methodological problems. First, though experimental research requires theories for framing hypotheses for testing, much of current experimental research is atheoretical. Without theories, the hypotheses being tested tend to be ad hoc, possibly illogical, and meaningless. Second, many of the measurement instruments used in experimental research are not tested for reliability and validity, and are incomparable across studies. Consequently, results generated using such instruments are also incomparable. Third, often experimental research uses inappropriate research designs, such as irrelevant dependent variables, no interaction effects, no experimental controls, and non-equivalent stimulus across treatment groups. Findings from such studies tend to lack internal validity and are highly suspect. Fourth, the treatments (tasks) used in experimental research may be diverse, incomparable, and inconsistent across studies, and sometimes inappropriate for the subject population. For instance, undergraduate student subjects are often asked to pretend that they are marketing managers and asked to perform a complex budget allocation task in which they have no experience or expertise. The use of such inappropriate tasks, introduces new threats to internal validity (i.e., subject’s performance may be an artefact of the content or difficulty of the task setting), generates findings that are non-interpretable and meaningless, and makes integration of findings across studies impossible.
The design of proper experimental treatments is a very important task in experimental design, because the treatment is the raison d’etre of the experimental method, and must never be rushed or neglected. To design an adequate and appropriate task, researchers should use prevalidated tasks if available, conduct treatment manipulation checks to check for the adequacy of such tasks (by debriefing subjects after performing the assigned task), conduct pilot tests (repeatedly, if necessary), and if in doubt, use tasks that are simple and familiar for the respondent sample rather than tasks that are complex or unfamiliar.
In summary, this chapter introduced key concepts in the experimental design research method and introduced a variety of true experimental and quasi-experimental designs. Although these designs vary widely in internal validity, designs with less internal validity should not be overlooked and may sometimes be useful under specific circumstances and empirical contingencies.

