Maths Foundations
Raquel Salmeron and Anita Frederiks
Figure 7.1 Maths Foundations. Image by Kc Rae, Aboriginal artist used under CC BY-NC-ND licence.
Introduction
Welcome to the Maths Foundations Chapter. Here you will find an introduction to fundamental mathematics (maths) concepts and principles applicable across a wide range of university disciplines. The chapter first discusses key arithmetic topics, introducing fundamental operations, the number system, place value, fractions, decimals, percentages, rounding, and more. Following this, there is a section focussed on numerical reasoning and problem solving, emphasising critical skills to successfully tackle mathematical problems. Finally, the chapter discusses techniques to develop mental maths skills to allow you to solve some maths problems “in your head”, which is a valuable skill in many practical situations.
Proficiency in arithmetic is essential in fields such as Science, Technology, Engineering, Mathematics and Medicine (STEMM). It also supports career paths that involve data analysis, finance, economics and programming. In essence, mastering these maths fundamentals will equip you with essential mathematical skills, practical knowledge, and problem-solving abilities, empowering you to tackle mathematical challenges, make informed decisions, and succeed in your academic and professional pursuits.
Arithmetic
Arithmetic is a fundamental branch of mathematics. Being comfortable with arithmetic operations including addition, subtraction, multiplication, and division enables you to perform calculations quickly and accurately, reducing your reliance on calculators or other tools. Mastering arithmetic concepts will allow you to confidently tackle more advanced branches of mathematics later in your studies, such as algebra, geometry, calculus and statistics.
Learning arithmetic promotes the development of logical thinking, pattern recognition, and mental agility. It enhances your memory, attention to detail, and the ability to think critically and analytically. These cognitive skills are transferable to various academic subjects and contribute to overall intellectual growth. Moreover, arithmetic is used in various aspects of your daily life, such as managing your finances, calculating bills, budgeting, shopping, cooking, and measuring.
Addition and subtraction

Addition is the process of combining two or more numbers to find their sum (or total).
Proficiency in addition supports mental math skills, enabling you to perform quick calculations mentally without relying on pen and paper or calculators. Table 7.1 shows the addition table. To use this table you find the first number of your sum on the left, and the second number of your sum on the top. Where the row and column intersect, is the result of the summation. For example, [latex]9+8 = 17[/latex].
Table 7.1 Addition table showing the sum of the number down the leftmost column and the number across the top row.
| [latex]+[/latex] | [latex]0[/latex] | [latex]1[/latex] | [latex]2[/latex] | [latex]3[/latex] | [latex]4[/latex] | [latex]5[/latex] | [latex]6[/latex] | [latex]7[/latex] | [latex]8[/latex] | [latex]9[/latex] |
|---|---|---|---|---|---|---|---|---|---|---|
| [latex]0[/latex] | [latex]0[/latex] | [latex]1[/latex] | [latex]2[/latex] | [latex]3[/latex] | [latex]4[/latex] | [latex]5[/latex] | [latex]6[/latex] | [latex]7[/latex] | [latex]8[/latex] | [latex]9[/latex] |
| [latex]1[/latex] | [latex]1[/latex] | [latex]2[/latex] | [latex]3[/latex] | [latex]4[/latex] | [latex]5[/latex] | [latex]6[/latex] | [latex]7[/latex] | [latex]8[/latex] | [latex]9[/latex] | [latex]10[/latex] |
| [latex]2[/latex] | [latex]2[/latex] | [latex]3[/latex] | [latex]4[/latex] | [latex]5[/latex] | [latex]6[/latex] | [latex]7[/latex] | [latex]8[/latex] | [latex]9[/latex] | [latex]10[/latex] | [latex]11[/latex] |
| [latex]3[/latex] | [latex]3[/latex] | [latex]4[/latex] | [latex]5[/latex] | [latex]6[/latex] | [latex]7[/latex] | [latex]8[/latex] | [latex]9[/latex] | [latex]10[/latex] | [latex]11[/latex] | [latex]12[/latex] |
| [latex]4[/latex] | [latex]4[/latex] | [latex]5[/latex] | [latex]6[/latex] | [latex]7[/latex] | [latex]8[/latex] | [latex]9[/latex] | [latex]10[/latex] | [latex]11[/latex] | [latex]12[/latex] | [latex]13[/latex] |
| [latex]5[/latex] | [latex]5[/latex] | [latex]6[/latex] | [latex]7[/latex] | [latex]8[/latex] | [latex]9[/latex] | [latex]10[/latex] | [latex]11[/latex] | [latex]12[/latex] | [latex]13[/latex] | [latex]14[/latex] |
| [latex]6[/latex] | [latex]6[/latex] | [latex]7[/latex] | [latex]8[/latex] | [latex]9[/latex] | [latex]10[/latex] | [latex]11[/latex] | [latex]12[/latex] | [latex]13[/latex] | [latex]14[/latex] | [latex]15[/latex] |
| [latex]7[/latex] | [latex]7[/latex] | [latex]8[/latex] | [latex]9[/latex] | [latex]10[/latex] | [latex]11[/latex] | [latex]12[/latex] | [latex]13[/latex] | [latex]14[/latex] | [latex]15[/latex] | [latex]16[/latex] |
| [latex]8[/latex] | [latex]8[/latex] | [latex]9[/latex] | [latex]10[/latex] | [latex]11[/latex] | [latex]12[/latex] | [latex]13[/latex] | [latex]14[/latex] | [latex]15[/latex] | [latex]16[/latex] | [latex]17[/latex] |
| [latex]9[/latex] | [latex]9[/latex] | [latex]10[/latex] | [latex]11[/latex] | [latex]12[/latex] | [latex]13[/latex] | [latex]14[/latex] | [latex]15[/latex] | [latex]16[/latex] | [latex]17[/latex] | [latex]18[/latex] |
Note, changing the order of addition does not change the resulting sum. For example: [latex]8+9 = 17[/latex] is the same as [latex]9+8 = 17[/latex].
Subtraction is the opposite of addition, that is, addition undoes subtraction, and subtraction undoes addition. Knowing the addition facts will help you with subtraction. For example,
[latex]7 - 4 = 3 \qquad \mbox{as} \qquad 3+4 = 7\,.[/latex]
Multiplication and Division
Multiplication is a shortcut for repeated addition. It allows you to find the total when adding the same number multiple times. For example, instead of adding [latex]4 + 4 + 4[/latex], you can simply multiply [latex]4 \times 3[/latex] to get the answer of [latex]12[/latex]. The number [latex]3[/latex] tells you the number of times you need to add the [latex]4[/latex] together (three times). This efficiency is crucial when dealing with large numbers or performing calculations quickly.
Division is the opposite of multiplication. This means that they undo each other’s effect. When you multiply a number by [latex]2[/latex] you get “twice” the value ([latex]3 \times 2 = 6[/latex]). On the other hand, dividing by two results in “half” the value ([latex]6 \div 2 = 3[/latex]). Note that after you multiply the [latex]3[/latex] by [latex]2[/latex], dividing the result ([latex]6[/latex]) by [latex]2[/latex] allows you to undo the effect and obtain the original number ([latex]3[/latex]).
In order to solve multiplication problems, you would need to know all the one-digit multiplication facts. Table 7.2 shows the multiplication of the number down the leftmost column and the number across the top row. It is important that you know the times tables so that you are ready to multiply larger numbers. Note that the order you multiply numbers is not important, that is [latex]3 \times 4 = 12[/latex] as does [latex]4 \times 3 = 12[/latex].
Table 7.2 Time tables, showing the product of the number down the leftmost column and the number across the top row.
| [latex]\times[/latex] | [latex]0[/latex] | [latex]1[/latex] | [latex]2[/latex] | [latex]3[/latex] | [latex]4[/latex] | [latex]5[/latex] | [latex]6[/latex] | [latex]7[/latex] | [latex]8[/latex] | [latex]9[/latex] |
|---|---|---|---|---|---|---|---|---|---|---|
| [latex]0[/latex] | [latex]0[/latex] | [latex]0[/latex] | [latex]0[/latex] | [latex]0[/latex] | [latex]0[/latex] | [latex]0[/latex] | [latex]0[/latex] | [latex]0[/latex] | [latex]0[/latex] | [latex]0[/latex] |
| [latex]1[/latex] | [latex]0[/latex] | [latex]1[/latex] | [latex]2[/latex] | [latex]3[/latex] | [latex]4[/latex] | [latex]5[/latex] | [latex]6[/latex] | [latex]7[/latex] | [latex]8[/latex] | [latex]9[/latex] |
| [latex]2[/latex] | [latex]0[/latex] | [latex]2[/latex] | [latex]4[/latex] | [latex]6[/latex] | [latex]8[/latex] | [latex]10[/latex] | [latex]12[/latex] | [latex]14[/latex] | [latex]16[/latex] | [latex]18[/latex] |
| [latex]3[/latex] | [latex]0[/latex] | [latex]3[/latex] | [latex]6[/latex] | [latex]9[/latex] | [latex]12[/latex] | [latex]15[/latex] | [latex]18[/latex] | [latex]21[/latex] | [latex]24[/latex] | [latex]27[/latex] |
| [latex]4[/latex] | [latex]0[/latex] | [latex]4[/latex] | [latex]8[/latex] | [latex]12[/latex] | [latex]16[/latex] | [latex]20[/latex] | [latex]24[/latex] | [latex]28[/latex] | [latex]32[/latex] | [latex]36[/latex] |
| [latex]5[/latex] | [latex]0[/latex] | [latex]5[/latex] | [latex]10[/latex] | [latex]15[/latex] | [latex]20[/latex] | [latex]25[/latex] | [latex]30[/latex] | [latex]35[/latex] | [latex]40[/latex] | [latex]45[/latex] |
| [latex]6[/latex] | [latex]0[/latex] | [latex]6[/latex] | [latex]12[/latex] | [latex]18[/latex] | [latex]24[/latex] | [latex]30[/latex] | [latex]36[/latex] | [latex]42[/latex] | [latex]48[/latex] | [latex]54[/latex] |
| [latex]7[/latex] | [latex]0[/latex] | [latex]7[/latex] | [latex]14[/latex] | [latex]21[/latex] | [latex]28[/latex] | [latex]35[/latex] | [latex]42[/latex] | [latex]49[/latex] | [latex]56[/latex] | [latex]63[/latex] |
| [latex]8[/latex] | [latex]0[/latex] | [latex]8[/latex] | [latex]16[/latex] | [latex]24[/latex] | [latex]32[/latex] | [latex]40[/latex] | [latex]48[/latex] | [latex]56[/latex] | [latex]64[/latex] | [latex]72[/latex] |
| [latex]9[/latex] | [latex]0[/latex] | [latex]9[/latex] | [latex]18[/latex] | [latex]27[/latex] | [latex]36[/latex] | [latex]45[/latex] | [latex]54[/latex] | [latex]63[/latex] | [latex]72[/latex] | [latex]81[/latex] |
Factors
Factors are all the numbers that multiply to get a particular number. For example, the factors of [latex]12\,[/latex], are all the numbers which multiply together with a result of [latex]12[/latex], that is: \begin{eqnarray*} 12 &=& 1 \times 12\,,\\ 12 &=& 2 \times 6\ \mbox{ and}\,,\\12&=&3\times 4\,.\end{eqnarray*} Therefore, the factors of [latex]12[/latex] are [latex]1[/latex], [latex]2[/latex], [latex]3[/latex], [latex]4[/latex], [latex]6[/latex] and [latex]12[/latex].
The Highest Common Factor (HCF) is the largest positive number that divides two or more numbers without leaving a remainder. For example, the HCF of [latex]12[/latex] and [latex]18[/latex] is [latex]6[/latex] because [latex]6[/latex] is the largest positive number that can divide both [latex]12[/latex] and [latex]18[/latex]. Similarly, the HCF of [latex]15[/latex], [latex]20[/latex], and [latex]25[/latex] is [latex]5[/latex] because [latex]5[/latex] is the largest number that can divide all three numbers evenly. The HCF is used when simplifying fractions.
The Lowest Common Multiple (LCM) is the smallest number that is a product of two or more numbers. For example, the LCM of [latex]4[/latex] and [latex]6[/latex] is [latex]12[/latex] because [latex]12[/latex] is the smallest number that is a multiple of both [latex]4[/latex] and [latex]6[/latex]. Similarly, the LCM of [latex]3[/latex], [latex]5[/latex], and [latex]7[/latex] is [latex]105[/latex] because [latex]105[/latex] is the smallest number that is a multiple of all three numbers. The LCM is often used in mathematics to find a common denominator for fractions or to solve problems involving periodic events that repeat at different intervals. For example, if one event occurs every [latex]3[/latex] days and another event occurs every [latex]4[/latex] days, the LCM of [latex]3[/latex] and [latex]4[/latex], which is [latex]12[/latex], represents the number of days after which both events will occur simultaneously.
Fractions

Think about situations where you need to divide something into equal parts, for example when sharing a pizza with your friends (see Figure 7.3).
Fractions help us describe and understand these divisions. Fractions also come into play when measuring ingredients for cooking, determining sale prices, calculating medications, and dealing with quantities that are not integers. Let’s consider a number of friends who are sharing a pizza, each having an equal portion of it. If there are two friends, each one will have half the pizza. That is, if we divide the pizza in two parts, each friend will get one of the two equal parts, or “one half” of the pizza (see Figure 7.4). The expression “one half” is written in maths as [latex]\frac{1}{2}[/latex], meaning that each friend has [latex]1[/latex] part of the [latex]2[/latex] parts the pizza has been divided into. Similarly, if there are four friends sharing the pizza, we would need to divide it in four parts, and each friend will get “one quarter” of it, which is written as [latex]\frac{1}{4}[/latex] (see Figure 7.5). We say that [latex]\frac{1}{2}[/latex] and [latex]\frac{1}{4}[/latex] are examples of fractions.


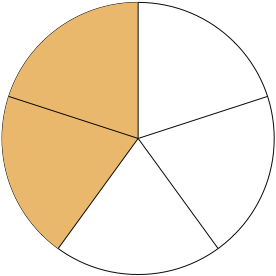
In general, a fraction is written as [latex]\frac{a}{b}[/latex], where [latex]a[/latex] and [latex]b[/latex] are integer numbers and [latex]b[/latex] is different from zero (written as [latex]b \neq 0[/latex], because division by zero is undefined in mathematics). In a fraction, [latex]a[/latex] (the top number) is called the numerator and [latex]b[/latex] (the bottom number) is called the denominator. A fraction is a way to represent parts of a whole. The denominator [latex]b[/latex] represents the number of equal parts the whole has been divided into (e.g. the two parts the pizza was divided into), and the numerator [latex]a[/latex] represents how many parts are considered (e.g. the one part given to each friend). So the fraction [latex]\frac{2}{5}[/latex] represents [latex]2[/latex] parts out of a total of [latex]5[/latex] the whole has been divided into (see Figure 7.6).
Adding and Subtracting Fractions
Now imagine that two friends have each [latex]\frac{1}{5}[/latex] of a pizza. How much of the pizza do they have in total? Putting the two [latex]\frac{1}{5}[/latex] slices together we realise that they have [latex]\frac{2}{5}[/latex] of the entire pizza (see Figure 7.7).
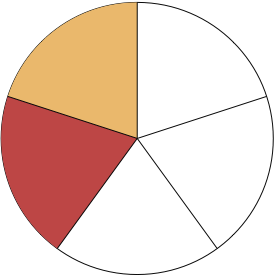
This leads us to an important concept: To add fractions, each fraction must have the same denominator, and to add them we add the numerators and keep the common denominator unchanged. That is: \[\frac{1}{5}+\frac{1}{5}=\frac{2}{5}\,.\]
Similarly, to subtract fractions (that share the same denominator), we subtract the numerators and leave the common denominator unchanged. For example, to find out how much pizza is left after the friends ate the two fifths they had, we calculate: \[\frac{5}{5}-\frac{2}{5}=\frac{3}{5}\,.\] We still have [latex]\frac{3}{5}[/latex] of the pizza, or [latex]3[/latex] of the total [latex]5[/latex] slices it was divided into. Note that the [latex]\frac{5}{5}[/latex] [latex](=1)[/latex] above corresponds to the “whole” (entire pizza) and we are subtracting the [latex]\frac{2}{5}[/latex] that has been eaten to find out what portion of it is still left.
In order to learn how to add or subtract fractions when their denominators are different, we need to first understand the concept of equivalent fractions.
Equivalent Fractions
Two fractions are equivalent when they represent the same portion of the whole. For example, the fractions [latex]\frac{2}{4}[/latex] and [latex]\frac{1}{2}[/latex] are equivalent, because they both represent one half of the whole. In the first fraction we consider two out of four parts, and in the second we consider one out of two parts, which both represents one half of the total number of parts we have (see Figure 7.8). This means that we should be able to convert one fraction to the other.
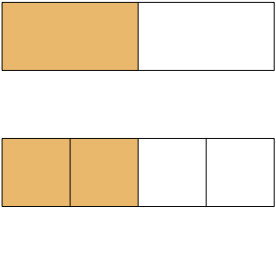
How can we use mathematics to change [latex]\frac{1}{2}[/latex] into [latex]\frac{2}{4}[/latex]? Or, how could you take a pizza that is cut into two pieces and cut it into four pieces? You could cut each of the two larger pieces into two smaller pieces. The whole pizza would then be cut into four pieces instead of just two. Mathematically, what we have described could be written as: \[\frac{1}{2}=\frac{1\times 2}{2\times 2} = \frac{2}{4}\,.\]So we may conclude that multiplying both the numerator and the denominator of a fraction by the same number does not alter the value of the fraction. This is the Equivalent Fractions Property.
You can use equivalent fractions to add or subtract fractions that have different denominators. You first need to transform the fractions to equivalent fractions that have the same denominator. For example,
[latex]\frac{1}{2}+\frac{1}{4}=\frac{1\times 2}{2\times 2}+\frac{1}{4}=\frac{2}{4}+\frac{1}{4}=\frac{3}{4}\,.[/latex]
Often, when you complete a calculation and obtain a fraction as your result, you will need to express the fraction in simplest form. A fraction is expressed in simplest form if the numerator and denominator cannot be simplified by dividing both of them by the same number (other than the number [latex]1[/latex]). In other words, the numerator and denominator do not have a common factor. If a fraction does have common factors in the numerator and denominator, you can reduce the fraction to its simplified form by removing (cancelling out) the common factors.
For example, consider the fraction [latex]\frac{2}{3}[/latex]. The factors of [latex]2[/latex] are [latex]2[/latex] and [latex]1[/latex] (that is, [latex]2 \times 1 = 2[/latex]), and the factors of [latex]3[/latex] are [latex]3[/latex] and [latex]1[/latex] (that is [latex]3 \times 1 = 3[/latex]). Because there are no common factors (not counting the number [latex]1[/latex]), the fraction [latex]\frac{2}{3}[/latex] is already in simplest form.
Now consider the fraction [latex]\frac{10}{15}[/latex]. The factors of the numerator and denominator are, respectively: \begin{eqnarray*}
10 &=& 2 \times 5\,, \qquad \mbox{and}\\
15 &=& 3 \times 5\,.
\end{eqnarray*}As you see, [latex]5[/latex] is a common factor of both [latex]10[/latex] and [latex]15[/latex]. So dividing both numbers by [latex]5[/latex] you obtain the fraction in simplified form. \begin{eqnarray*} \frac{10}{15} &=& \frac{10 \div 5}{15 \div 5} \\ &=& \frac{2}{3}\,. \end{eqnarray*}Note that you can also obtain this result substituting the numerator and denominator of the fraction by the product of its factors and cancelling the common factor (the number [latex]5[/latex] that appears both in the numerator and the denominator): \begin{eqnarray*} \frac{10}{15} &=& \frac{2 \times \cancel{5}}{3\times \cancel{5}} \\ &=& \frac{2}{3}\,. \end{eqnarray*}
Multiplying and Dividing Fractions
Multiplication of fractions is particularly useful when you need to calculate proportions, scale measurements, or solve real-world problems involving quantities that are not whole numbers.
For example, let’s consider the multiplication of the fractions one half [latex]\left(\frac{1}{2}\right)[/latex] and three quarters [latex]\left(\frac{3}{4}\right)[/latex] or \[ \frac{1}{2} \times \frac{3}{4}\,.\]You may think about this as “a half of” [latex]\frac{3}{4}[/latex]. To find one half of three-quarters, you would divide the [latex]\frac{3}{4}[/latex] (that is, three [latex]\frac{1}{4}[/latex] pieces of the “whole”) into two equal halves, then take one of the halves as your solution. This operation can be visualised in Figure 7.9. Now, since you cannot divide three [latex]\frac{1}{4}[/latex] pieces evenly into two parts, you would need to first convert [latex]\frac{3}{4}[/latex] into an equivalent fraction, for example by multiplying the numerator and denominator by [latex]2[/latex], giving: \[\frac{3 \times 2}{4 \times 2} = \frac{6}{8}\,.\]Now, taking half of the six [latex]\frac{1}{8}[/latex] pieces gives three [latex]\frac{1}{8}[/latex] pieces, written mathematically as [latex]\frac{3}{8}[/latex].
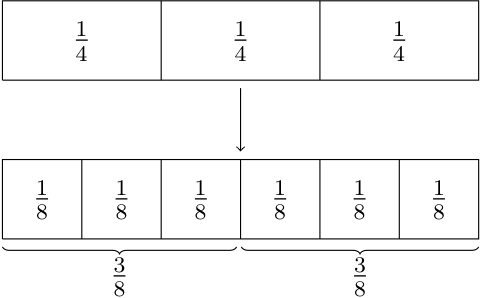
Therefore, \[ \frac{1}{2} \times \frac{3}{4} = \frac{3}{8}\,.\]Note that we could also find this solution by multiplying together the numerators and denominators of the fractions: \[\frac{1}{2} \times \frac{3}{4} = \frac{1 \times 3}{2 \times 4} = \frac{3}{8}\,.\]This observation is a general property: To multiply fractions, we multiply the numerators and multiply the denominators. Remember to check that your solution is in simplest form and if not, convert the fraction to simplest form.
Looking at another example, to find the product of [latex]\frac{2}{3}[/latex] and [latex]\frac{3}{4}[/latex], you would do:\begin{eqnarray*}\frac{2}{3}\times \frac{3}{4}&=& \frac{2 \times 3}{3 \times 4} \\ &=& \frac{6}{12}\,.\end{eqnarray*}Notice that both [latex]6[/latex] and [latex]12[/latex] have a common factor of [latex]6[/latex], that is [latex]12 = 6 \times 2[/latex], and [latex]6 = 6 \times 1[/latex]. Therefore, you can simplify the answer to be:\begin{eqnarray*}\frac{6}{12} &=& \frac{1 \times 6}{2 \times 6} \\&=& \frac{1}{2}\,.\end{eqnarray*}This result is already in simplest form, so this is the final answer.
Finally, let’s discuss division of fractions. This operation allows you to determine how many times one fraction is contained within another. When we divide one fraction by another, we essentially ask the question: “How many of the second fraction can fit into the first fraction?”
First, let’s consider an example of dividing an integer by a fraction: \[2 \div \frac{1}{4}\,.\]This expression is asking “How many quarters are there in two.” One whole is [latex]4[/latex] quarters, so [latex]2[/latex] is [latex]8[/latex] quarters. Therefore, [latex]2 \div \frac{1}{4} = 8\,.[/latex] In a similar way, [latex]12 \div 3 = 4[/latex] because there are three groups of [latex]4[/latex] in [latex]12[/latex] [latex]\left(3 \times 4 = 12\right)[/latex].
Now, consider the division \[\frac{1}{2} \div \frac{1}{6}\,.\]We need to figure out how many [latex]\frac{1}{6}[/latex]‘s there are in [latex]\frac{1}{2}[/latex]. This can be shown visually in Figure 7.10.
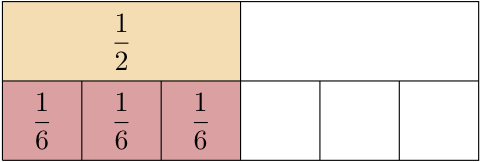
Note that \[ 3 \times \frac{1}{6} = \frac{3}{1} \times \frac{1}{6} = \frac{3 \times 1}{6 \times 1} = \frac{3}{6} = \frac{1}{2}\,. \]So \[\frac{1}{2} \div \frac{1}{6} = 3\,.\]
Notice that [latex]\frac{1}{2}\times \frac{6}{1} = 3[/latex] also, with [latex]\frac{6}{1}[/latex] known as the reciprocal of [latex]\frac{1}{6}[/latex]. It can be shown that this is a general result, so to divide fractions, multiply the first fraction by the reciprocal of the second.
Another way to write fractions is to use decimals. This concept, along with place value will be discussed in the next section.
Place value and decimals
Place value is used to represent the value of digits within a number based on their position or place in the number. In our decimal number system, which is based on powers of [latex]10[/latex], each digit’s position within a number determines its place value. For example, consider the number [latex]358[/latex]:
- The digit [latex]3[/latex] is in the hundreds place, so its place value is [latex]3 \times 100 = 300\,.[/latex]
- The digit [latex]5[/latex] is in the tens place, so its place value is [latex]5 \times 10 = 50\,.[/latex]
- The digit [latex]8[/latex] is in the ones place, so its place value is [latex]8 \times 1 = 8\,.[/latex]
When these place values are added together [latex](300 + 50 + 8)[/latex], you get the total value of the number, which is [latex]358[/latex]. This can be shown in a place value table (see Table 7.3).
Decimals are a way of representing numbers that have a fractional part. A decimal number consists of a whole number part and a decimal part, separated by a decimal point. The decimal point indicates the boundary between the whole number and fractional parts of the number. The digits to the left of the decimal point represent whole numbers and the digits to the right of the decimal point represent fractions of a whole number. This can be seen in Table 7.3. For example, in the number [latex]3.142[/latex], [latex]3[/latex] is the whole number part and [latex]0.142[/latex] is the decimal part. The place value of the decimal numbers can be found in a similar way to the previous example:
- The digit [latex]3[/latex] is in the ones place, so its place value is [latex]3 \times 1=3\,.[/latex]
- The digit [latex]1[/latex] is in the tenths place, so its place value is [latex]1 \times 0.1 = 0.1\,.[/latex]
- The digit [latex]4[/latex] is in the hundredths place, so its place value is [latex]4 \times 0.01 = 0.04\,.[/latex]
- The digit [latex]2[/latex] is in the thousandths place, so its place value is [latex]2 \times 0.001= 0.002\,.[/latex]
When these places values are added together, [latex](3 + 0.1 + 0.04 + 0.002)[/latex], you get the total value of the number, [latex]3.142[/latex]. This can be seen in Table 7.3.
Table 7.3 Visualisation of the numbers [latex]358[/latex] and [latex]3.142[/latex] as part of the base [latex]10[/latex] number system
| Thousands [latex]1,000[/latex] |
Hundreds [latex]100[/latex] |
Tens [latex]10[/latex] |
Ones [latex]1[/latex] |
[latex]\bullet[/latex] | Tenths [latex]0.1[/latex] |
Hundredths [latex]0.01[/latex] |
Thousandths [latex]0.001[/latex] |
|---|---|---|---|---|---|---|---|
| [latex]3[/latex] | [latex]5[/latex] | [latex]8[/latex] | |||||
| [latex]3[/latex] | [latex]\bullet[/latex] | [latex]1[/latex] | [latex]4[/latex] | [latex]2[/latex] |

Decimals are commonly used in everyday life, such as in measurements, currency, and percentages. They are also important in many fields, including science, finance, and engineering. They can be added, subtracted, multiplied, and divided just like whole numbers. They can also be represented as fractions or percentages.
Percentages
In mathematics, a percentage is a way of expressing a number as a fraction of [latex]100[/latex] (per cent meaning “per hundred”). For example, [latex]5\%[/latex] means [latex]\frac{5}{100}[/latex]. It is important to be able to convert numbers to percentage, or convert a percentage back to numbers.
When converting to a percentage, form a fraction and multiply by [latex]100\%[/latex]. For example, a student receives [latex]15[/latex] marks out of a total of [latex]20[/latex] for an assignment. As a percentage, he receives: \[ \frac{15}{20} \times 100\% = 75\%\,.\]
When converting from a percentage to a fraction or decimal you divide the percentage amount by [latex]100[/latex]. For example: Convert [latex]65\%[/latex] to a fraction and a decimal. To convert a percentage to a fraction, divide by [latex]100[/latex]: \[ 65\% = \frac{65}{100} = \frac{13}{20}\,\]where the rightmost fraction has been expressed in simplest form. To convert to a decimal: \[ 65\% = \frac{65}{100} = 65 \div 100 = 0.65\,.\]Note when dividing by [latex]100[/latex], you shift the decimal place two places to the left.
Rounding numbers
Rounding is used to get an approximate answer to more complex calculations or to ensure that your answer has the correct level of accuracy. To round a number to a specified place value, investigate the digit to the immediate right of that place. If this digit is:
- the number [latex]0[/latex], [latex]1[/latex], [latex]2[/latex], [latex]3[/latex], or [latex]4[/latex], the specified place value remains unchanged.
- the number [latex]5[/latex], [latex]6[/latex], [latex]7[/latex], [latex]8[/latex] or [latex]9[/latex], round up the specified place value by [latex]1\,.[/latex]
For example, when rounding [latex]734[/latex] to the nearest ten, you first need to check the digit in the ones place. This number is [latex]4[/latex]. As [latex]4[/latex] is between [latex]0[/latex] and [latex]4[/latex], which means the number in the tens place remains the same, that is [latex]734 = 730[/latex], rounded to the nearest ten. You could also use the approximately equals to symbol [latex](\approx)[/latex] to write this mathematically, \[734 \approx 730\,.\]
Rounding with decimal numbers follows the same rule. If you want to round [latex]123.456[/latex] to the nearest tenth (or to one decimal place), you look at the digit in the hundredths place (second decimal place), which is the place value directly to the right of the first decimal place. This digit is a [latex]5[/latex]. This means you need to round up the digit in the tenths place, that is: [latex]123.456 = 123.5[/latex], rounded to the first decimal place, or [latex]123.456 \approx 123.5[/latex].
When doing calculations, it is good practice to have in your head what the approximate answer should be. Rounding is an effective way to get that approximate answer. To apply this method, first round the numbers involved in the calculation, then calculate. For example, to multiply [latex]234[/latex] by [latex]726[/latex], round to [latex]234 \approx 200[/latex] and [latex]726 \approx 700[/latex], making the product: \[200 \times 700 = 14,000\,,\]suggests: \[234\times 726 \approx 14,000\,.\]Therefore, once you have done the product (by hand, or on your calculator), if your answer is vastly different from [latex]14,000[/latex], you should check your working. Rounding is also important for many mental maths techniques, as shown in the Mental Maths Skills section.
When doing calculations, you should use all the decimal places your calculator has to ensure accuracy of your final answer. One of the most asked questions is how many decimal places should be given in the final answer. As a rule of thumb, you should always give your answer to the same level of accuracy as the data provided. For example, you want to find the average height of six people (in centimetres), \[ 172.5\quad 177.8 \quad 169.2 \quad 180.0 \quad 162.5 \quad173.7\] and your calculations result in an answer of [latex]172.616\, 666\, 7[/latex]. As all the heights were given to one decimal place, you would also give your answer to one decimal place. That is, the average height is [latex]172.6[/latex] centimetres.
Order of Operations
Mathematical expressions are written to convey specific information. Therefore, it is important that everyone reading them interprets them the same way and arrives at the same answer. For example, what is the answer to the expression [latex]15 + 12\div 3[/latex], is it [latex]9[/latex] or [latex]19[/latex]? For this reason, mathematicians have established a convention (an accepted method) that specifies the order in which operations are to be performed.
This order of operations states: When working from left to right follow these steps:
- Evaluate any expressions in brackets. (If there are brackets inside another set of brackets, do the inside brackets first.)
- Evaluate any powers and roots. Examples of powers are squares, e.g. [latex]4^2 = 4\times 4 = 16[/latex], examples of roots include square and cube roots e.g. a square root is [latex]\sqrt{16} = 4[/latex] and a cube root is [latex]\sqrt[3]{8} = 2[/latex], as [latex]2^3 = 8[/latex].
- Evaluate any multiplications or divisions.
- Evaluate any additions or subtractions.
Back to the above example: \[ 15 + 12\div 3\,. \]The first operation you will complete is the division: \begin{align*} & 15 + 12\div 3 \\ &= 15 + 4\,. \end{align*}You can complete the addition: \[15 + 4 = 19\,.\] Therefore, [latex]15 + 12\div 3 =19[/latex] not [latex]9[/latex].
Let’s look at another example: calculate \[8-12\div (7-4\times 2)\,.\] The first step would be to evaluate the brackets. Within the brackets, also follow the order of operations, so solve the multiplication first then the subtraction; that is: \begin{align*}&8-12\div (7-4\times 2) \\&= 8-12\div (7-8) \\&= 8-12\div -1\,,\end{align*}next complete the division:\begin{align*}& 8-12\div -1 \\&= 8 – (-12) \\&= 8 + 12\,,\end{align*}and finally, complete the addition: \[ 8 + 12 = 20\,. \]
You can also evaluate expressions using margin notes, for example,\begin{align*}& \sqrt[3]{125} \times 3 -(6^2 – (4 + 3)^2 + 11) \\&= \sqrt[3]{125} \times 3 – (6^{2} – 7^{2} + 11) & & \mbox{Evaluate the inside bracket,} \\&= \sqrt[3]{125} \times 3 – (36 -49 +11) & & \mbox{Evaluate the powers in the brackets,} \\&= \sqrt[3]{125} \times 3 – (-2) & & \mbox{Evaluate the brackets, left to right,} \\&= 5 \times 3 + 2 & & \mbox{Evaluate root & minus negative,} \\ &= 15 + 2 & & \mbox{Evaluate the multiplication,} \\&= 17 & & \mbox{Evaluate the addition.}\end{align*}
Modern scientific calculators will follow the order of operations. It is still important to be able to work your way through the process to allow you to think mathematically and apply problem solving skills to further mathematics, for example algebra.
Numerical Reasoning and Problem Solving
Numerical reasoning and problem solving are important skills for your studies. Numerical reasoning is the ability to handle and interpret numerical data. This includes manipulating, analysing and drawing conclusions from data, which may be presented in words, tables or graphs. Problem solving usually involves understanding a worded question, translating it into mathematics, applying a mathematical procedure to obtain an answer, and finally interpreting and communicating your result.
In order to improve your problem solving skills, master the required fundamental mathematical concepts, learn key problem solving strategies and practise key calculations, not only during your formal learning activities, but also in everyday life. This is a key step!
Let’s do an example: Joseph bought [latex]4[/latex] sheets of stamps. Each sheet had [latex]20[/latex] stamps. How many stamps did Joseph buy? To solve the problem, you would
- write a phrase describing the result that we are looking for: The total number of stamps, given by the product of the number of sheets and the number of stamps per sheet,
- translate the statement into maths notation: [latex]4 \times 20[/latex],
- calculate the result: [latex]4 \times 20 = 80[/latex],
- check that the result is reasonable. If each sheet has [latex]20[/latex] stamps, and Joseph bought [latex]4[/latex] of them, it is reasonable that the result is [latex]4[/latex] times [latex]20[/latex], which is [latex]80[/latex], and
- write a sentence to express the result: Joseph bought [latex]80[/latex] stamps.
Mental Maths Skills
Mental maths is the ability to conduct numerical reasoning quickly and accurately, in order to solve a problem “in your head”.
This ability is beneficial for a wide range of studies, including for example aviation and paramedicine, where you will need to perform calculations in your head and at times, under pressure. Therefore, mastering numerical reasoning and mental maths is an important part of your studies.
In order to solve a problem in your head, you may want to first solve the problem using pen and paper, then repeat it using mental maths techniques, explained below. It may be also very useful to practice your mental maths skills during your everyday activities, e.g. when paying at the supermarket (Can you estimate what your total expense will be?) or travelling in your car (If my speed is [latex]60[/latex] kilometres per hour, how long would it take you to travel [latex]100[/latex] kilometres?).
To develop or further improve your mental maths abilities, try the following techniques, which have been adapted and expanded from the discussion in McElroy (2004):
- Master key mathematical concepts. These include fundamental operations (addition, subtraction, multiplication, division, operations with powers and roots).
- Solve the problem first using pen and paper, following the steps described in the Problem Solving Section in previous chapter.
- Put away the paper and visualise the step-by-step process to find the solution.
- Practice, using different numbers or solving for a different aspect of the problem, until you feel comfortable that you can reproduce the process accurately and in a timely manner
- Grade your problems, so that you start with simple ones, and progressively move to more complex ones.
- Keep practising!
You may simplify calculations using rounding techniques. Consider adding the numbers [latex]67 + 44[/latex]. To simplify this calculation, instead of adding [latex]67 + 44[/latex], you could round the numbers to the closest tens (e.g. [latex]10[/latex], [latex]20[/latex], [latex]30[/latex], etc.) and then correct for the rounding you have done. This is a very efficient technique to do arithmetic in your head. How would this work with the example above?
- Add the numbers rounded to the closest tens (e.g. add [latex]70 + 40 = 110[/latex]).
- Calculate the round off differences.
- Difference from [latex]70[/latex] to [latex]67[/latex]: subtract [latex]3[/latex] to the answer.
- Difference from [latex]40[/latex] to [latex]44[/latex]: add [latex]4[/latex] to the answer.
- Adjust the result to obtain the final answer [latex]110 - 3 + 4 = 111[/latex].
Conclusions
Through this chapter, you saw the importance of developing your fundamental mathematical skills. This chapter focused on the foundations of arithmetic, including working with fractions, and developing your mental maths. These fundamental skills are easily integrated not only into your studies, but also into your everyday life.
Key points
- It is important to develop your number facts (addition, subtraction, multiplication and division) as these skills are vital in problem solving and mental maths techniques.
- Addition and subtraction of fractions require a common denominator.
- Equivalent fractions are different ways to write the same fraction.
- Fractions as answers should always be given in simplest form.
- When multiplying fractions, multiply the numerators and denominators.
- Dividing fractions is the same as multiplying by the reciprocal of the second fraction.
- Round your answers to the specified number of decimal places, or to the required level of accuracy for the question.
- You must follow the order of operations when evaluating mathematical problems.
- When solving a worded problem, write a phrase describing the result you are looking for, translate the information you have into mathematics, then calculate, check and interpret your result.
- Practice “mental maths” skills by solving problems using pen and paper first, then visualising the process to find the solution. Round off techniques may be useful here.
Glossary of key maths terms
Addition: The process of finding the total amount or quantity when you join two or more numbers. Other words used to mean addition include: sum, total, add, plus, and. The symbol used for addition is the plus sign ([latex]+[/latex]).
Decimal: A decimal number is the fractional part of a number, fractions of powers of ten, such as tenths, hundredths, thousandths, and so on. For example, one quarter [latex]\left(\frac{1}{4}\right)[/latex] can also be written as [latex]0.25[/latex] in decimal form.
Denominator: The denominator is the bottom part of the fraction and represents the total number of equal parts that make up a whole.
Division: Division is the process of finding out how many times one number is contained within another number, and what is left over after the division (remainder). The result of a division operation is called the quotient. It is denoted by the division symbol ([latex]\div[/latex]) or sometimes using a horizontal line (a fraction), e.g. [latex]12\div 3[/latex] can be written as [latex]\frac{12}{3}\,.[/latex]
Equation: In mathematics, an equation is a mathematical statement that states the equality of two expressions. For example, [latex]2 \times 3^2 + 6 = 24\,,[/latex] is an equation.
Equivalent fraction: Equivalent fractions have different numerical representations but correspond to the same portion of a whole or a quantity.
Evaluate: In mathematics, evaluate means to find the numerical value or result of a mathematical expression or equation.
Expression: In mathematics an expression is a combination of numbers, variables, operators, and symbols that represents a mathematical phrase or statement. An expression does not contain an equals sign. For example: [latex]15+ 12 \div 3[/latex] is an expression.
Factor: Factors are all the numbers that multiply to get a particular number. In other words factors are numbers which can be divided into a number without leaving a remainder.
Fraction: A fraction is a mathematical expression that represents a part of a whole or a division of a quantity into equal parts.
Fraction in simplest form: A fraction is in its simplest form, also known as its simplest or lowest terms, when the numerator and the denominator have no common factors other than [latex]1[/latex]. In other words, the fraction cannot be further reduced without changing its value.
Highest Common Factor: The Highest Common Factor (HCF), also known as the Greatest Common Divisor (GCD), is the largest positive number that divides two or more numbers without leaving a remainder. In other words, it’s the largest number that is a common factor of the given numbers.
Integer: An integer is a whole number that can be either positive, negative, or zero, without any fractional or decimal parts. Integers include all the positive whole numbers, their negative counterparts, and zero.
Lowest Common Multiple: The Lowest Common Multiple (LCM), also known as the Least Common Multiple, is the smallest positive multiple that is divisible by two or more numbers. In other words, it’s the smallest number that is a multiple of the given numbers.
Mental maths: Mental maths refers to the practice of performing mathematical calculations mentally, without the use of external tools such as paper, pencil, or a calculator. It involves using mental strategies, techniques, and shortcuts to solve mathematical problems quickly and accurately in one’s head.
Multiplication: Multiplication is a shortcut for repeated addition. It is denoted by the times symbol ([latex]\times[/latex]) Other words for multiplication include times, product, multiply, or multiples.
Negative numbers: Negative numbers are numbers less than zero. Negative numbers have a negative sign, for example [latex]-2[/latex] is two below zero.
Numerical reasoning: Numerical reasoning is a cognitive skill that involves the ability to understand, analyse, and interpret numerical information in various contexts. It encompasses the capacity to perform mathematical calculations, make sense of quantitative data, and draw logical conclusions based on numerical information.
Numerator: The numerator is the top part of the fraction and represents the number of parts being considered.
Percentage: A way of expressing a number as a fraction of [latex]100[/latex] (per cent meaning “per hundred”).
Positive numbers: Positive numbers are numbers which are larger than zero.
Powers: In mathematics, a power refers to the expression of a number (known as the base) raised to a certain exponent (also called the power or index). The power indicates the number of times the base is multiplied by itself. For example,
- [latex]2^3[/latex] represents [latex]2[/latex] raised to the power of [latex]3[/latex] which is: [latex]2 \times 2 \times 2 = 8[/latex].
- [latex]5^2[/latex] represents [latex]5[/latex] raised to the power of [latex]2[/latex] which is: [latex]5 \times 5 = 25[/latex].
Real numbers: Real numbers encompass all the numbers that can be found on the number line, both to the right and left of zero.
Reciprocal: The reciprocal of a number is another number that, when multiplied by the original number, results in a product of [latex]1[/latex]. In other words, the reciprocal of a nonzero number [latex]a[/latex] is [latex]\frac{1}{a}[/latex]. For example the reciprocal of [latex]2[/latex] is [latex]\frac{1}{2}[/latex], because [latex]2 \times \frac{1}{2} = 1[/latex]. Another example is the reciprocal of [latex]\frac{3}{4}[/latex] is [latex]\frac{4}{3}[/latex], because \[\frac{3}{4} \times \frac{4}{3} = 1\,.\]
Remainder: A remainder is anything left over after completing a division. This is normally rewritten as a remainder, or a fraction, or decimal. For example, [latex]12\div 5 = 2[/latex] remainder of [latex]2[/latex], or [latex]12\div 5 = 2\frac{2}{5} = 2.4[/latex].
Root: The most common roots are the square root ([latex]\sqrt{\quad }[/latex]) and the cube root [latex]\sqrt[3]{\quad }[/latex]), corresponding to powers of [latex]2[/latex] and [latex]3[/latex], respectively. Roots are essentially the inverse operation of powers. Roots can also be referred to as surds.
- the square root of [latex]25[/latex] is: [latex]\sqrt{25} = 5[/latex], as [latex]5^2=25[/latex].
- the cube root of [latex]8[/latex] is: [latex]\sqrt[3]{8} = 2[/latex], as [latex]2^3 = 8[/latex].
Rounding: Rounding is the process of approximating a number to a specified degree of accuracy.
Subtraction: Finding the difference between two numbers is called subtraction. It is denoted by the minus sign ([latex]-[/latex]).Other words used to mean subtraction include minus, take, from, subtract, difference, take away.
GLOSSARY OF COMMON SYMBOLS USED IN MATHS
[latex]+[/latex] Plus sign (Addition)
[latex]-[/latex] Minus sign (Subtraction)
[latex]\times[/latex] Times sign (Multiplication)
[latex]\div[/latex] Divided by sign (Division)
[latex]=[/latex] Equals or equal to
[latex]\approx[/latex] Approximately equal to
[latex]\neq[/latex] Not equal to (different from)
[latex]\mathbb{Z}[/latex] Symbol used to represent all Integer numbers
[latex]\mathbb{R}[/latex] Symbol used to represent all Real numbers
SUMMARY OF KEY MATHEMATICAL OPERATIONS
Addition [latex]1 + 3 = 4[/latex], [latex]a + b = c[/latex]
Subtraction [latex]3 - 1 = 2[/latex], [latex]a - b = c[/latex]
Multiplication [latex]2 \times 3 = 6[/latex], [latex]a \times b = c[/latex]
Division [latex]4 \div 2 = 2[/latex], [latex]a \div b = c[/latex] where [latex]b \neq 0[/latex]
Adding Fractions \[\frac{a}{b} + \frac{c}{b} = \frac{a+c}{b}\]
Subtracting Fractions \[ \frac{a}{b} – \frac{c}{b} = \frac{a-c}{b}\]
Multiplying Fractions \[ \frac{a}{b} \times \frac{c}{d} = \frac{a\times c}{b\times d}\]
Dividing Fractions \[\frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \times \frac{d}{c} = \frac{a\times d}{b \times c}\]
Equivalent Fractions \[\frac{a}{b} = \frac{a \times c}{b \times c}\]
Cancelling terms (numerator and denominator) \[ \frac{a \times \cancel{c}}{b \times \cancel{c}} = \frac{a}{b}\]
Converting to a percentage from a fraction or decimal, multiply by [latex]100\%[/latex].
Converting a fraction or decimal to a percentage, divide by [latex]100[/latex].
REFERENCES
McElroy, R. D. (2004). Mental math for pilots : a study guide. Aviation Supplies & Academics.
ACKNOWLEDGEMENTS
Some content in this chapter was drawn from Prealgebra 2e (OpenStax), licensed under a CC BY 4.0 licence. We would also like to acknowledge our colleague Rowena McGregor for her valuable feedback on this chapter.

