Chapter 6, Part A. Constructing and Appraising Arguments
Learning Objectives
- Understand the distinction between ‘relations among ideas’ and ‘matters of fact’
- Understand the nature of categories or classes
- Be able to identify subject and predicate in propositions
- Be able to distinguish between the four types of categorical propositions (a, e, i, and o)
- Be able to distinguish between distributed and undistributed subjects and predicates
- Be able to identify minor, major, and middle terms
- Be able to apply the six rules of categorical syllogisms.
New Concepts to Master
- Truth-preserving
- Categories and classes
- Syllogism
- Major premise
- Minor premise
- Quantifier
- Subject term
- Copula
- Predicate term
- The universal affirmative
- The universal negative
- The particular affirmative
- The particular negative
- Distribution
- Minor, major, and middle term.
Chapter Orientation
Welcome to Chapter 6. By this point, you know quite a bit about arguments and logic in a general sense, but in this chapter, we’ll look closely at several specific types of arguments and why and when they do and don’t work.
This chapter will most likely be the hardest one in this book. It contains the most technical information that students typically struggle with. Things do get easier for our final two chapters, but this one will take some time to absorb and properly understand (stick with it – the payoff is well worth it). I expect you’ll need to go over this chapter more than once, as well as watch the videos (located in the additional resources in Chapter 6 Part B) several times, before you master this material.
As you’re progressing through the material, some of you might wonder why you need to learn all of these technicalities. The reason is that they expose the mechanics of propositions and arguments necessary for understanding why and how they work, and more importantly – why and how they don’t work. Kind of like learning some of the technicalities of an engine to help you understand how to diagnose and resolve its problems. Beginning in Chapter 2, I pointed out that the conclusions of sound deductive arguments are necessarily certain. I showed the difference between inductive and deductive reasoning. I explained what formal and informal fallacies were and how you might spot them. I also discussed the necessity of falsification for scientific reasoning and the fact that confirmation in scientific reasoning is logically fallacious. While you might have taken all of this on faith, as you should have learned by now, trusting me blindly is never a very good idea. So this chapter (while a little heavy and dry) will give you the actual reasons why all of those things I said are true.
There’s quite a bit of grammar in this chapter. This might also seem strange in a critical thinking text, however, how we express our propositions and how we organise them into arguments makes all the difference to the validity of our inferences. Two groups of statements that, on the surface, might seem to say the same thing, actually have different logical properties. For example:
I find insects frightening.
That’s an insect.
Therefore, I am frightened.
This argument is expressed sloppily, and the inference to its conclusion is not as certain as it could be. However, rephrasing the propositions and organising them differently creates a definitive and valid deductive conclusion. For example:
All insects are frightening.
This is an insect.
Therefore, this is frightening.
This chapter will guide you through the reasons and rules that make up the differences between these two arguments. Understanding this will allow you to you formulate your thoughts and arguments in a way that makes them bulletproof.
Let’s retrace some of the key points we’ve learned so far about arguments and logic to make sure we’re all starting out on the same page. As everyone knows, logic can be confusing, as the following famous quote from Through the Looking-Glass expresses quite nicely. There’s a good chance this is how you’ll feel about logic by the end of this chapter, but I promise that with some dedicated study, anyone can master this stuff.

This first part will be a little repetitive as we try to cement what you already know before moving into deeper waters. You can skip forward if you’re confident you know the basics already.
- Every claim about the world is a proposition, and a proposition is defined as a statement that can be true or false.
- An argument is a piece of reasoning that’s expressed using a group of statements (it’s a series of statements, the purpose of which is to convince people that something – a conclusion – is true).
- Logic is the science of dissecting and understanding arguments.
- To qualify as an argument, at least two propositions are required, one being the conclusion and the other being its premise.
- Argument here doesn’t mean dispute or fight, but rather a piece of reasoning that attempts to establish a certain proposition (a conclusion) on the basis of other propositions (premises that contain reasons and evidence).
- A proposition must rest on an argument to be taken seriously (even if the argument isn’t stated).
- A proposition without a supporting argument might still be true, but we can’t be sure, and without knowing the premises, we don’t really know why it would be true.
- For this reason, claims are assertions that are only as believable as the arguments they depend on.
- The propositions that serve as the premises of an argument contain the reasons and evidence that are intended to make the conclusion ‘believable’.
- The truth of each premise rests on their own arguments and when there is no argument supporting them, they’re ‘unsupported assumptions’. Remember, unsupported isn’t the same as saying it’s true or false, but merely that it doesn’t have any supporting evidence or reasoning to back it up.
- An inference is the leap of reasoning from things that are taken to be known (premises) to some new knowledge (conclusion). Even if the conclusion isn’t very new, your belief in it might be new and strengthened by way of inference from the premises.
- Arguments are evaluated in two ways:
- Their ‘truth’ – which is a product of how true or believable the premises are.
- Their ‘validity’ – which is a matter of the inferential jump from premises to conclusion.
- Arguments that satisfy both conditions – that is, with true premises and valid inferences – are called ‘sound’.
- The strongest valid arguments are deductive, and these arguments are called ‘truth-preserving’, which is a fancy phrase that means the truth of the premise guarantees or forces the truth of the conclusion. In this way, the truth of the premises is preserved or passed on to the conclusion.
‘Truth-preserving’ is a fancy way of describing the type of argument in which when the premises are true, truth-ness is carried over to the conclusion. This is the standard, valid deductive form of argument we’ve become familiar with since Chapter 2. It’s impossible for true premises in a valid deductive argument to produce a false conclusion. The truth of the premises is preserved in the conclusion.
- Inductive arguments are a weaker, but more common type of argument. They’re formally invalid because they’re not ‘truth-preserving’ since they can have true premises, but a false conclusion.
- In appraising arguments, the truth of the premises is a matter of assessing their believability based on either:
- Scientific evidence, for premises that are empirical propositions (e.g. ‘Children learn best with interactive activities’)
- Reasoning for premises that are rational propositions (e.g. ‘All children are mortal’ is a truth of reason alone’).
- In appraising arguments, the validity of the inference is a matter of assessing whether the premises make the conclusion true or believable.
- For deductive arguments, validity is an all or nothing property.
- In a valid deductive argument, this is quite easy because the premises force the conclusion to be true. If the argument is valid, it’s impossible for the conclusion to be false if the premises are true, and this is the test for validity of deductive arguments.
- For inductive arguments, validity is more a matter of ‘degrees of strength’.
- In a valid inductive argument, this is a matter of ‘degrees of believability’. It’s possible to have a false conclusion with true premises, but with many strong premises, the truth of the conclusion should get more and more believable.
- A fallacious argument is one where the inference isn’t valid.
- For deductive arguments, fallacies are a matter of the conclusions not being necessarily true even if the premises are true.
- This is called a formal fallacy because the problem is with the form of the argument, not its content (not what the statements say, but how they connect).
- You can check this by removing the content of the statements and exchanging the things (terms) in the statements with symbols such as p, q, x, y, etc. After doing this, a formal fallacy will still be present.
- For inductive arguments, fallacies are a matter of how applicable and useful the premises are in supporting the conclusion. These are called informal fallacies because the problem is with the content of the premises (what they say), and less a matter of the form of the argument, or how the sentences connect.
- You can check this by removing the content of the statements and exchanging them with symbols such as p, q, x, y, etc. After doing this, an informal fallacy is unlikely to still be apparent.
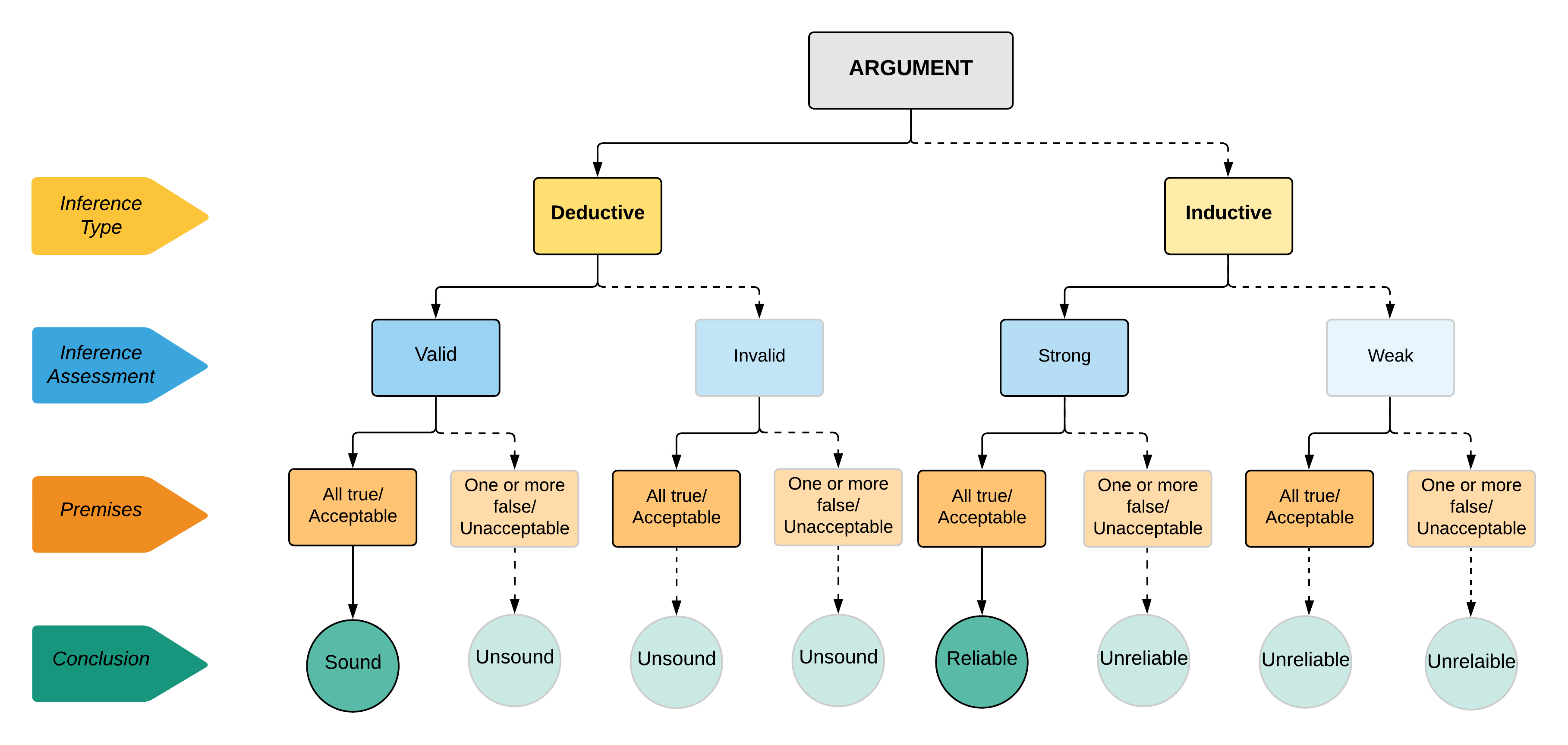
- Sometimes we don’t use the language of validity with inductive arguments because they’re by nature formally invalid. Rather, we talk of the inferences as either strong or weak, which is a matter of how convincing they are. Similarly, sometimes the terms ‘reliable’ and ‘unreliable’ are used in place of ‘sound’ and ‘unsound’ for inductive arguments (see Figure 6.1).
- Sound deductive arguments give us certainty in the conclusion, but do so at the price of limited scope. In this way, they’re merely explicative.
- Explicative means to explicate or clarify the implication of the premises, and therefore, these arguments don’t really provide new knowledge.
- Genuinely new knowledge can be obtained with induction, but the price paid is that of certainty. In this way, inductive arguments are ampliative.
- Ampliative means to amplify or expand our knowledge beyond the premises.
The decision tree below (Figure 6.2) is a good way to summarise some of these points. You’ll notice I use the words “reliable” and “unreliable” to describe inductive arguments. This is because, unlike deductive arguments, there’s no guarantee that a true starting point in an inductive argument leads to a true conclusion. So, how good an inductive argument is depends on two things: how convincing it feels to you (there is a subjective element to this decision) and how often it accurately predicts what happens in the real world. When an inductive argument is both convincing and accurate, we call it “cogent”, which means clear, logical, and convincing.
At this point, you’re probably wondering why this is all so important – why we’ve spent almost the whole course on propositions and arguments. Remember, all claims or assertions are propositions, and all propositions rest on arguments for their veracity. Therefore, understanding the value of propositions and the credibility of the arguments that underpin them is the central work of critical thinking.
This is information we all enter this chapter with. Let’s review last chapter’s content before launching into some new stuff.
Chapter 5 Review
The topic of the last chapter was language, thought, and concepts. We set the scene initially with a couple of nifty little quotes from Wittgenstein, who said things like ‘The limits of my language mean the limits of my world’ and ‘Whereof one cannot speak, thereof one must be silent’. Next, we established the importance of language to our everyday life – it serves as the contents and vehicles of our thought, our understanding of the world, our beliefs, and our communication with each other. We defined language as a rule-governed abstract system of arbitrary symbols that are agreed upon by the community to reference or signify specific things (our internal psychological world, as well as the outside world). The ability to abstract and represent ideas and concrete things enables the two great achievements of human cognitive evolution: to think and to communicate. The abstraction of concrete ‘things’ to the symbolic is incredibly useful as it gives us the ability to manipulate, contemplate, and communicate symbols and signs rather than concrete things, which are not so malleable by contrast.
However, the abstracting power of language – while affording us enormous advantages – comes at the cost of those things we think and communicate about being forever disconnected or separated from the concrete things these words represent. Importantly, however, abstraction to the symbolic means we can think about things that we aren’t immediately experiencing (e.g. ‘the future’). We can also think about things that we could never possibly experience, such as purely abstract concepts like ‘zero’ and ‘infinity’, or more interesting things like ‘life after death’.
Some interesting insights emerged as implications from our definition. Firstly, that language is only meaningful to those who are part of the community or social group that agree to adopt the symbols proposed by that system. Secondly, that the definitions of the symbols and signs are purely subjective in a community or social sense. While we can’t have private definitions of words, a community or a social group who want to communicate and think together have subjective meanings for words. In this way, definitions are not objective or fixed –this is why dictionaries update definitions every year.
Another important feature of language that is rather counterintuitive is that languages are only internally meaningful because their signs are purely self-referential. This means that the symbols and signs of our language only have meaning inside the systems they’re part of. Symbols only ever point to other symbols – never to real things. As such, the meaning of words is only other words. This is because words are abstract and arbitrary self-referential symbols that never get outside the system to point to something concrete. Words only ever point to other signs and symbols in the language system.
In this way, the meaning of words within a language is holistic, just like beliefs. Their meaning partly comes from how they connect to each other and other parts of the web of signs. Similarly, in many cases, the meaningfulness of language is sentence-sized, rather than individual word-sized. In this way, words get much of their meaning from their role in sentences – what’s referred to as syntactic meaning. The second way words have any meeting is pragmatic, which is to say that the meaning of a word comes from how it’s used. Semantic meaning is the third way words have meaning, and this is captured in the meanings of individual words and their connection with the things they signify or symbolise. Semantic meaning is something a bit more like the meaning of the term ‘in and of itself’, although we saw that this is flexible and subject to change as meaning is modified by both syntactic (meanings change according to the sentence a word is used in) and pragmatic influences (meanings change according to how the term is used and the context in which it’s used).
The extent to which language influences our thoughts and experiences is more controversial, and it can be quite profound. One perspective on language’s influence is known as the Sapir-Wolf hypothesis. This hypothesis is also known as linguistic determinism, which is to say that language determines our thoughts and experiences. This hypothesis maintains that language predetermines what we see in the world around us. This is a much stronger form of the linguistic influence perspective represented in the quotes from Wittgenstein at the beginning of the chapter. Wittgenstein didn’t argue that our language creates our experiences, but rather puts boundaries around them and restricts how we make sense of them and what we can say about them.
Language influences perception in a range of different ways. The symbols we have at our disposal to catalogue, describe, and understand our experiences have an influence on the nature of those experiences. Language influences what we pay attention to, how much attention we give to things in our perceptual field, what importance we attribute to them, and what subsequent thoughts and beliefs we have about them. We also came across some interesting research on differences in colour perception between people from different cultures.
Beliefs are another area where language has an enormous impact. Beliefs are made up of words and words are part of how these beliefs are catalogued, stored, and connected. The meaning of the terms that make up beliefs link to each other in the same way that hydrogen and oxygen atoms connect to make up water molecules. There are limitations imposed by the linguistic nature of beliefs on the things we can actually have beliefs about. We simply can’t have beliefs about things we don’t have words or symbolic representations for.
This can sometimes explain why it’s difficult for us to relinquish beliefs that are no longer useful. Part of the meaningfulness of the words we use lies in how they make up our beliefs. Words and symbols get their meaning due to their semantic, syntactic, and pragmatic functions inside the web of belief. Certain beliefs are protected from falsification (even though they may be falsified by experience) simply because they’re so necessary to the very meaning of some of our words (and consequently, our world).
An important consideration about language for critical thinking – as well as for science – is concepts. Concepts are abstract ideas or principles that are the fundamental building blocks of our thinking and understanding about the world, as well as of our scientific knowledge. Concepts can be relatively simple, like ‘joy’ or ‘money’ (though money isn’t so simple in the modern day with blockchain currencies and all), to very complex concepts like ‘intelligence’ or ‘the meaning of life’. We’ve been introduced to tons of concepts so far in this text, and they are still many more to go. When you learn new concepts, you get new thinking powers and skills, new ways or modes of understanding the world, new ways of conceptualising things, of expanding your horizons, and of opening you up to new experiences, and a new language to describe and communicate all of this.
Throughout the history of science, revolutions have mostly represented a changing of concepts and a redefinition of our key terms and symbols which we use to represent and understand the world. But a change of concept definitions is actually something like a change of subject matter. An important type of concept for those of you studying psychology is psychological constructs. The term ‘constructs’ here betrays the sense that these are simply human-made conventions that are formulated to make sense of and communicate something important. Once we have psychological constructs to understand and communicate things better, we have a more definite sense of what’s going on psychologically inside ourselves and other people. However, reification is a constant risk. This sometimes happens to scientific concepts when we forget that they’re artificial formulations, not representing anything more than our own ideas. The risk is that we take a concept as the concrete real thing (which may turn out not to exist, like ego depletion) we want to represent, rather than simply as a man-made conventional construction that’s useful for a restricted period of time. Remember, concepts are just like disposable razors that are only worth holding on to as long as they remain useful.
Finally, we looked at language as a rhetorical tool. The power of language to shape our thoughts and behaviour is a simple outgrowth of the power of language to influence all thinking, experiences, and perspectives generally. Language is a powerful tool that we use in our day-to-day life, as well as having to confront its use by other people. Specific uses of language as a rhetorical tool include the use of emotive and colloquial language. Emotive language is the use of specific words to elicit an emotional experience in the audience. It isn’t necessarily the use of emotion terms – it doesn’t need to describe emotions at all. Emotive language as a persuasive tool rarely refers to an emotion itself, but uses certain words and symbols to make other people have certain emotional experiences. Another rhetorical use of language is colloquial language, which is simply the use of everyday casual language to be more persuasive. People use informal language to try to bring others onside and make them more receptive to their message.
Back to Hume’s Fork
Remember from Chapter 4 that Hume explained that reasoning and knowledge can be about two things: relations of ideas and matters of fact. Propositions that deal with either relations of ideas or matters of fact are known as analytic or synthetic propositions, respectively (see Figure 4.4). I also discussed how deductive reasoning is capable of establishing relations of ideas, whereas inductive reasoning is required to establish matters of fact. This chapter follows on from this division by demonstrating some forms of deductive and inductive arguments and illustrating the principles of each.
Deductive Arguments
Earlier, we described deductive arguments as necessarily truth-preserving. This is a function of them being nonampliative. In basic terms, a valid deductive argument is one where if the premises are accepted as true, we must accept the conclusion as true because the conclusion says nothing that wasn’t said, at least implicitly, in the premises.
The most common types of deductive arguments are categorical and conditional (or hypothetical) forms. The first ever (and most famous) example of deductive reasoning is the categorical syllogism, so naturally, we’ll start there.
Categorical Syllogisms
Aristotle invented the categorical syllogism, and it remains one of the most fundamental forms of argumentation. Classical deductive (or Aristotelian) logic is based on the idea of classes or categories, which are nothing more than groups of things. Categorical syllogisms involve propositions that are called categorical propositions, which affirm or deny that a whole or part of a class is included in another. I’ll explain this soon, so don’t sweat it if that sentence made zero sense to you.

This will all be more familiar to you than you might realise. In fact, we’ve come across many categorical syllogisms already in this text, since it’s the most straightforward type of deductive argument. Every time I’ve taught you about deductive arguments, I’ve used a categorical syllogism as an example.
The most famous example is as follows:
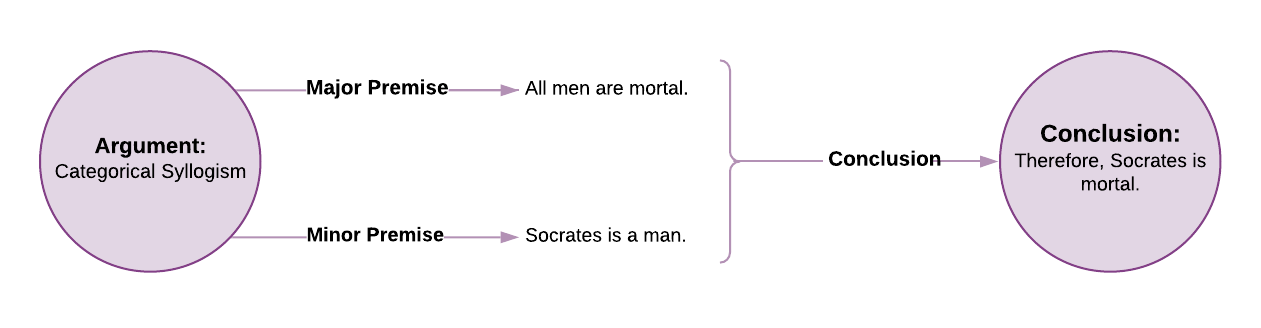
The format of every categorical syllogism is three categorical propositions (two premises and a conclusion), as illustrated below:
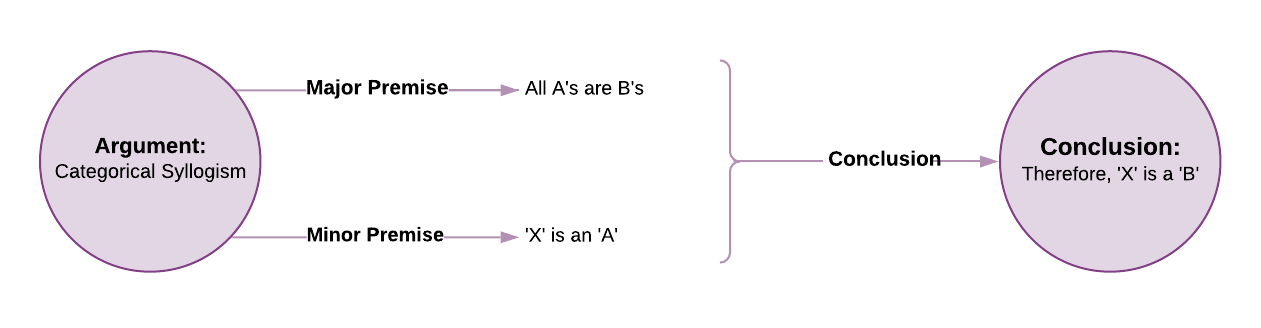
The so-called categories or classes are ‘men’, ‘things that are mortal’, and ‘Socrates’ (even though this last category has just the one guy in it). All categorical syllogisms deal with three categories or classes like this. The technical term for them is ‘terms’. When we talk about the ‘terms’ of a syllogism, we’re talking about the groups, categories, or classes that are being described, but now we’re getting ahead of ourselves.
‘Categories’ and ‘Classes’: As the name suggests, categorical syllogisms deal with categories, which are classes or groups of things. The concept of category here is broad, and even includes groups or classes with only a single thing in them – in this way, almost anything can be a category. By this account, I am a category that contains just one item or entity (me). This may seem weird at first, but it’s useful to think in this way in order to wrap your head around the rules and fallacies of categorical syllogisms. As you might expect, categorical propositions are the building blocks of categorical syllogisms. That is, the propositions make claims about categories or classes of things belonging (or not belonging) to other classes or categories of things. To state it more formally, a categorical proposition makes a claim (asserting or denying) that members of one class or category are included in another class or category. The proposition ‘Michael is a lecturer’ refers to two categories (‘Michael’ and ‘lecturers’) and proposes that the first category (the category of Michael) is part of the second category (the category of lecturers). These categories referred to in categorical propositions are called ‘terms’.
As you can see, a categorical syllogism has three propositions (this is actually a fixed rule), two of which are premises and the third is the conclusion. The first premise is called the major premise and the second premise is called the minor premise. Note that major here doesn’t mean more important – it just means the first premise. It might as well be called the number one premise, but historically, it has been called the ‘major premise’, and it usually contains a universal statement (the same is true for the major term, which is the non-middle term in the major premise, but more on this later).
‘Major premise’ and ‘Minor premise’: A categorical syllogism involves three propositions: major premise, minor premise, and conclusion. Each of these propositions contains two categorical terms (names of classes or categories). Most often, the major premise is the first premise, and the minor premise is the second premise.
The more technical designation of one of the premises as major and one as minor has to do with their role in the conclusion. The major premise is the premise containing the major term, and the major term is determined by whatever is the predicate term in the conclusion. Similarly, the minor premise is the premise containing the minor term and the minor term is determined by whatever is the subject in the conclusion. I know this sounds complicated, but it will become clearer once we go over the concepts of ‘subject’, ‘predicate’, and ‘major’ and ‘minor’ terms.
You already know from previous chapters that for the deductive argument to be valid, it must have a conclusion that can’t possibly be false if the premises are true. That is, the premises have to be stated in such a way that a conclusion drawn from them can’t possibly be untrue. But now we’ll learn why this is the case, as well as the background rules that give syllogisms this special quality.
Four Types of Categorical Propositions
Categorical syllogisms follow an ‘A is part of C, and all As are Bs, then B is part of C type of logic’. They’re called categorical because the propositions they contain relate two categories or classes (groups of things). Categorical syllogisms involve properties (a predicate) that things (subjects) have, and therefore, make the subjects part of certain categories or groups represented by those properties. For this reason, a categorical syllogism contains what are called categorical propositions (the ‘A is part of C, and all As are Bs, then B is part of C’ I mentioned above).
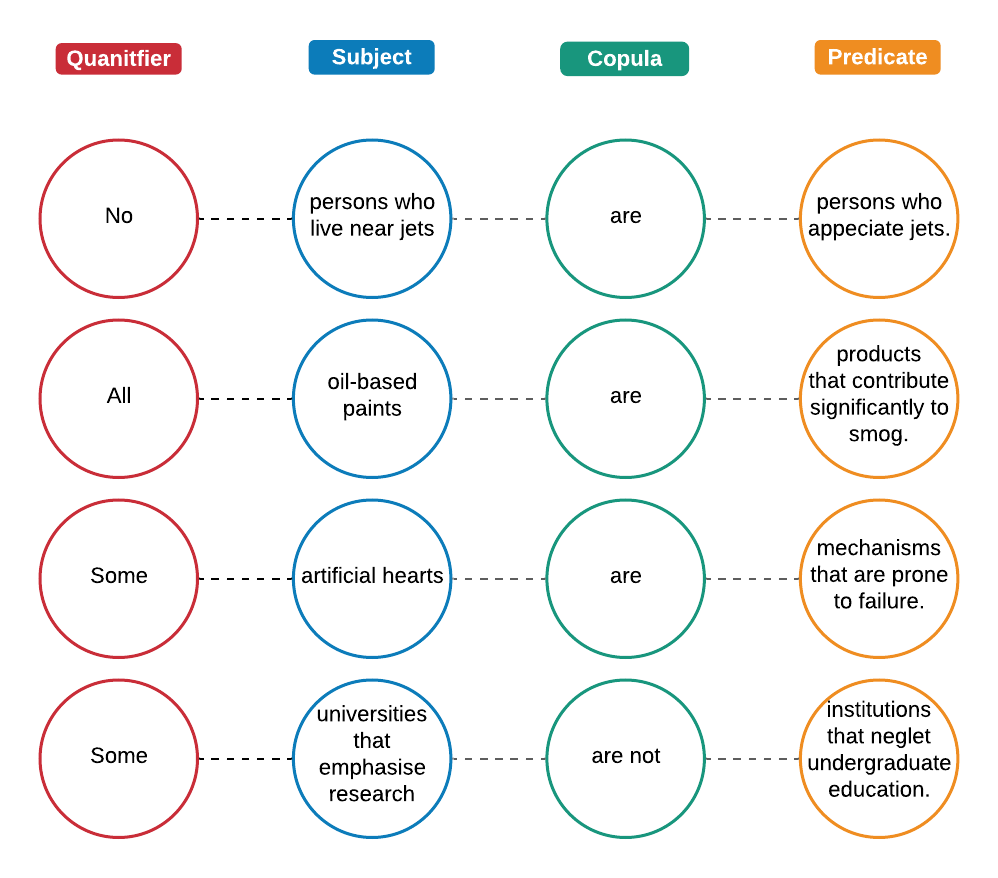
Some example categorical propositions: ‘No persons who live near airports are persons who appreciate the noise of jets’, ‘All oil-based plants are products that contribute significantly to photochemical smog’, ‘Some artificial hearts are mechanisms that are prone to failure’, and ‘Some universities that emphasise research are not institutions that neglect undergraduate education’.
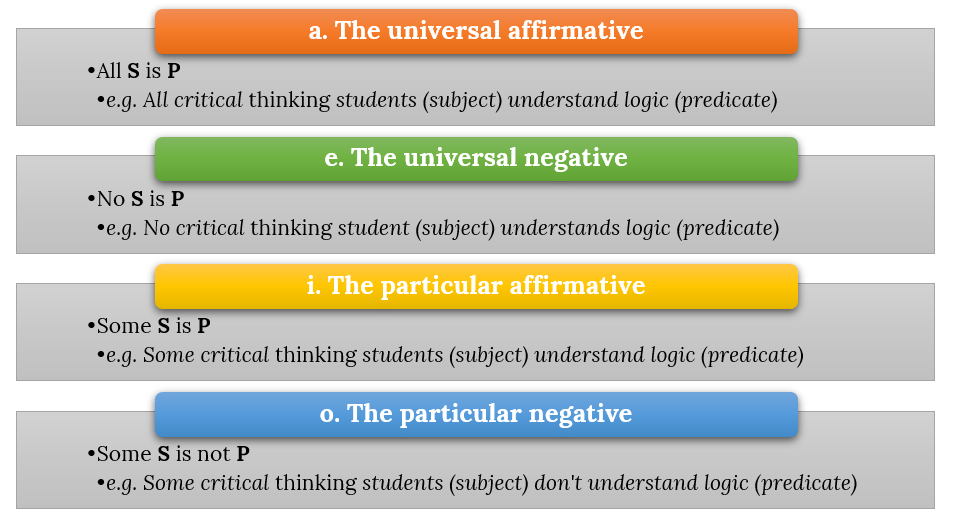
There are four types of categorical propositions that simply vary the quantity of things (universal versus particular) being described (using the quantifier part of the sentence – the word ‘all’ or ‘some’), as well as the quality (affirmative or negative) of being or having something or not (using the copula part of the sentence –the word ‘are’ or ‘are not’). These four types of propositions are called type ‘a’, ‘e’, ‘i’, and ‘o’ (I don’t know why they’re lettered only with vowels like this).
a. The universal affirmative: Every member (universal) of one class or category is (affirmative) also a member of a second class or category.
e. The universal negative: No member (universal negative) of one class or category is a member of a second class or category.
i. The particular affirmative: Some members (particular) of one class or category are (affirmative) also a member of a second class or category.
o. The particular negative: Some members (particular) of one class or category are not (negative) members of a second class or category.
You can see that the four types of categorical propositions differ in regard to (1) the quantity, which is how many of the subject category or group (some, all, or none), and (2) the quality – whether they are or are not part of a second group or category, and thus affirmative or negative.
There are a series of rules that govern valid syllogisms, and a formal fallacy will have been committed if any of these rules are violated. Remember, formal fallacies relate mostly to deductive arguments and concern the structure or format of the argument. It has nothing to do with what the premises say, and that’s why you can swap the actual information for symbols (a, b, c, etc.). There are six such rules that make a syllogism valid. Before we move on to the actual rules, though, we need to clarify some technical terms.
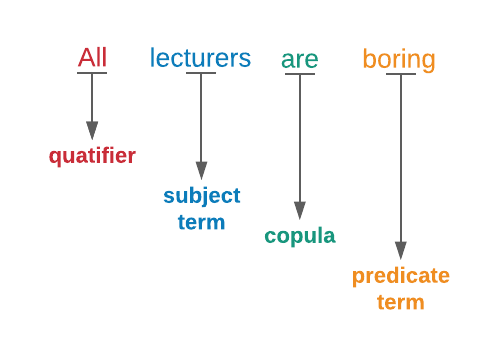
‘Quantifier’, ‘Subject term’, ‘Copula’, and ‘Predicate term’: All categorical propositions contain these ingredients. Remember that a categorical proposition makes claims about categories or classes of things belonging (or not belonging) to other classes or categories. This is achieved by indicating a quantity of the category we are talking about (usually all, some, or none). This is the quantifier. The subject term in a statement is often the first noun and is the thing we’re talking about or describing in the proposition. The copula is the next in line, and is a Latin word meaning ‘link’ or ‘tie’. A copula is often a verb and is needed to link the subject to the predicate (usually the copula is a simple ‘is’ or ‘is not’, or ‘are’ or ‘are not’). Finally, the predicate term – often a noun or adjective – is the attribute or property category we want to claim the subject category does or doesn’t have or belong to.
The subject term is the category of things being defined. The predicate term is the definition or description being given – the category the subject is proposed to belong to. The quantifier tells us how much of the subject category we’re talking about (all, some, or none). The copula affirms or denies the subject as belonging to the predicate category. Let’s look at an example proposition: ‘All logic is boring’. The first term is the quantifier, and we learn from this that ‘all’ not ‘some’ or ‘none’ of logic is what’s being talked about. The subject term of the sentence (what is being described) is the category or class of things called ‘logic’. The copula ‘is’ then helps us know what is being said about the subject, while the predicate term ‘boring’ is the description being given. Like all categorical propositions, this declaration is talking about two categories of things and linking them in some way. To express this in the language of ‘categories’: all the categories of things that are ‘logic’ belong to the category of things that are ‘boring’. Figure 6.5 illustrates this structure using the sentence ‘All lecturers are boring’.
‘Term’: This technical term seems a little self-referential. I have to apologise here for all the grammar, which I know is tedious and sleep-inducing, but we don’t have much choice if we’re going to understand and evaluate claims about the world. A term is just the label that refers to a category or class. In the proposition ‘All men are mortal’, the terms ‘men’ and ‘mortal’ refer to classes or groups of things, whereas ‘all’ is the quantifier that tells us how many (the quantity, which is the same thing as the amount) of the subject class are being referred to (men are the subject in this sentence). The term ‘are’ is the copula, as it connects the subject and predicate. In a categorical proposition, asking, ‘How many classes or categories are being referred to?’ is the same as asking ‘How many terms are there?’. At the start of this section, I described categorical syllogisms as following an ‘A is part of C, and all As are Bs, then B is part of C type of logic’. The A, B, and C here are terms and simply refer to classes or categories of things.
‘Distributed’: This is sometimes called ‘Distribution of Terms’. Distribution can be an attribute of either subjects or predicate terms in a proposition, and means every member of a class or category is denoted (or referred to) by the term. Propositions are called ‘distributed’ if they have a term that refers to all members of the category or class (or make a claim about all members).
For any category (whether it be the subject or predicate), we could be referring to all members, and if we’re saying something about the entire category, this category term is then distributed. It’s often easy to work out if the subject term is distributed by checking to see if the proposition is a universal proposition, which means it refers to all members of the subject category. If I claim ‘All dogs are cute’, the subject term ‘dogs’ is distributed because I’m talking about all of them. Determining whether the predicate term is distributed or not is a little more difficult. My claim that ‘All dogs are cute’ has dogs as the subject term and cute as the predicate term. The subject is distributed, but the predicate ‘cute’ isn’t because the claim doesn’t say something about all cute things – there are cute things like kittens that are not included in my claim.
So now we have the concepts of subject and predicate at our disposal, we can use them to once again review our four types of categorical propositions.
The statement ‘Quality, quantity, and distribution tell us what standard form categorical propositions assert about their subject and predicate terms – not whether those assertions are true’ is important to keep in mind.
‘The universal affirmative’, ‘The universal negative’, ‘The particular affirmative’, and ‘The particular negative’: Recall that categorical propositions are statements that affirm or deny that one category belongs to another. These four main types of categorical propositions are arrived at by interchanging different quantifiers and copulas. Each of these propositions differs in quantity (amount), which is determined by the quantifier, and quality (affirming or denying), which is determined by the copula.
‘Particular’ or ‘universal’ is the quantity of the predicate category we’re referring to. It’s universal if we’re referring to ‘all’ or ‘none’, and particular if we’re referring to ‘some’. ‘Affirmative’ or ‘negative’ refers to whether we’re claiming this subject category has the predicate attribute (belongs to the predicate category) or doesn’t have the predicate attribute (doesn’t belong to the predicate category).
For completeness, let’s work out the possible Distributions of Terms in each of the four types of propositions (summarised in Figure 6.7). When we use the quantifiers ‘all’ or ‘no’ (i.e. ‘none’) for the subject, we have a distributed subject because we’re talking about all members of that subject term or group. In this case, when the subject is met with an ‘all’ quantifier, it’s a distributed subject term, but not a distributed predicate. When a predicate is preceded by the ‘not’ copula, it’s a distributed predicate term because it’s saying something about the whole class of the predicate (that none of them are part of the subject group or class). As a result, you can work out that only proposition type E has both a distributed subject and predicate.
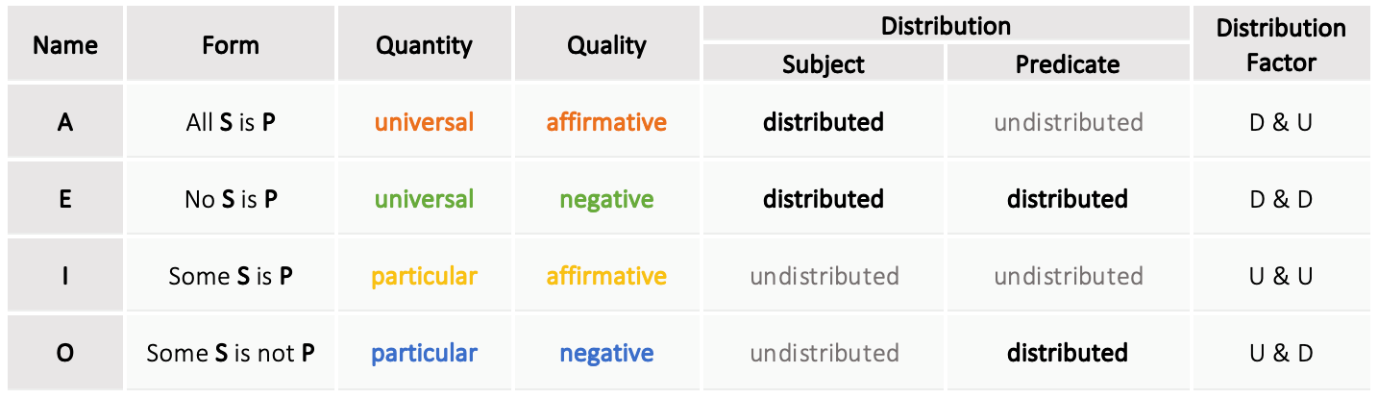
The key to understanding the validity of syllogisms is called the distribution factor, which is whether the subject or predicate are distributed or not (the rules will call on the distribution a lot). For example, in type A propositions, the distribution factor is D and U to mean the subject is distributed, but the predicate isn’t.
Let’s see some examples of propositions and their parts:
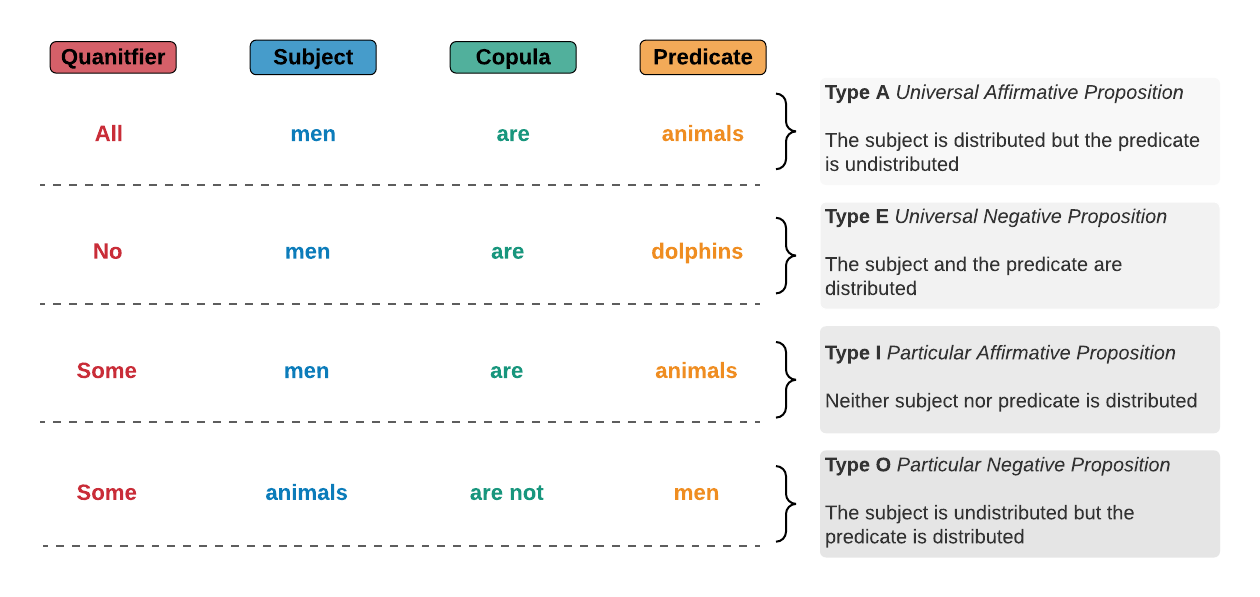
- You know that the first one above is a type A categorical proposition because it proposes that all members of a class (men) are members of another class (animals).
- You know that ‘men’ is the subject and ‘animals’ is the predicate.
- You also know that the subject term ‘men’ is distributed (it’s distributed within the class of animals), while the predicate term ‘animals’ is undistributed because the statement makes no claim about all members of the class of animals (there is nothing being said about other animals).
- The terms ‘all’ is the quantifier and the term ‘are’ is the copula.
You’ll now have noticed that the propositions all have a very predictable form. We can call that form ‘Q, S, C, and P’, which stands for ‘Quantity, Subject, Copula, and Predicate’. The inclusion of all of these ingredients doesn’t really vary – it’s the terms that change (different things being referred to). Sometimes in real-world propositions, these terms are ordered differently, but all four are necessary for a correct categorical proposition. Determining the type of proposition we’re dealing with has to do with the quantity (‘all’, ‘none’, ‘some’, etc.) and the copula (‘are’ and ‘are not’) that connects the subject and predicate (copula comes from the same Latin root as ‘copulate’). No other kinds of words can be used as copulas except connective words like ‘are’, ‘are not’, ‘is’, and ‘is not’.
Let’s take another look at the example categorical propositions I introduced earlier:
When syllogisms are sound (true premises and valid inference), they yield certain conclusions – the Holy Grail of all knowledge endeavours. However, for a syllogism to achieve this outcome, it must possess specific characteristics, which we call rules. For example, a valid syllogism employs exactly three terms or three classes or categories, and each term is used exactly twice. The terms are labelled minor, major, and middle. An analysis of categorical syllogisms begins by looking at the conclusion, which is where we find the minor and major term, but not the middle term. When the syllogism is written correctly, the middle term is easy to find by looking for the term the two premises share that doesn’t feature in the conclusion. One of the three terms of a valid syllogism must be used as the subject term in the conclusion. This is called the minor term because it’s actually the non-middle term in the minor premise. One other term must be used as a predicate term in the conclusion. This is called the major term because it’s actually the non-middle term in the major premise. The third term of the syllogism doesn’t appear in the conclusion at all, but must be employed somewhere in both premises. This is called the middle term because its job is to link (be in the middle of) the two premises to launch the conclusion.
To summarise:
- The subject term of the conclusion is the minor term.
- the predicate term of the conclusion is the major term.
- the term not used in the conclusion is the middle term, and this has to feature in both premises.
So when talking about syllogisms, there are major and minor premises as well as major, minor, and middle terms (I get that this can be confusing, but with more examples and some practice, we might be able to wrap our heads around it –some worked examples are the in the last part of this chapter).
Now we have covered the fact that categorical syllogisms contain three propositions: one major (or first) premise, one minor (or second) premise, and one conclusion. Among these three propositions, the major term appears twice, the minor term appears twice, and the middle (or connective tissue) term appears twice – no more, no less!
‘Minor, major, and middle term’: These terms are the names of the categories or classes that are the subjects and predicates of categorical propositions. Each of these three term types is mentioned exactly two times. The designation of a term as ‘minor’, ‘middle’, or ‘major’ is a product of the role it plays in the conclusion of a categorical syllogism. The major term is the predicate of the conclusion. The minor term is the subject of the conclusion. The middle term is the third term in a categorical syllogism, which doesn’t appear in the conclusion. A shortcut way of working out which is the major and minor term is knowing that the major premise almost always comes first in the syllogism, and the major premise is the premise with the major term. The minor premise almost always comes second, and the minor premise contains the minor term. If the syllogism is valid, the middle term is the term not appearing in the conclusion.
The problem with evaluating everyday argument is that people are rarely so kind so as to present their arguments in this convenient way. So we need to dissect arguments and convert them into this formal syllogism format in order to properly evaluate them.
Let’s identify these terms and their characteristics.

Rules and Fallacies of Categorical Syllogisms
There are some rules about how you use these terms to avoid fallacies and guarantee the truth of your conclusion (if you do your own reading on this, you’ll come across sets of five, six, or seven rules, but they just about all say the same thing).
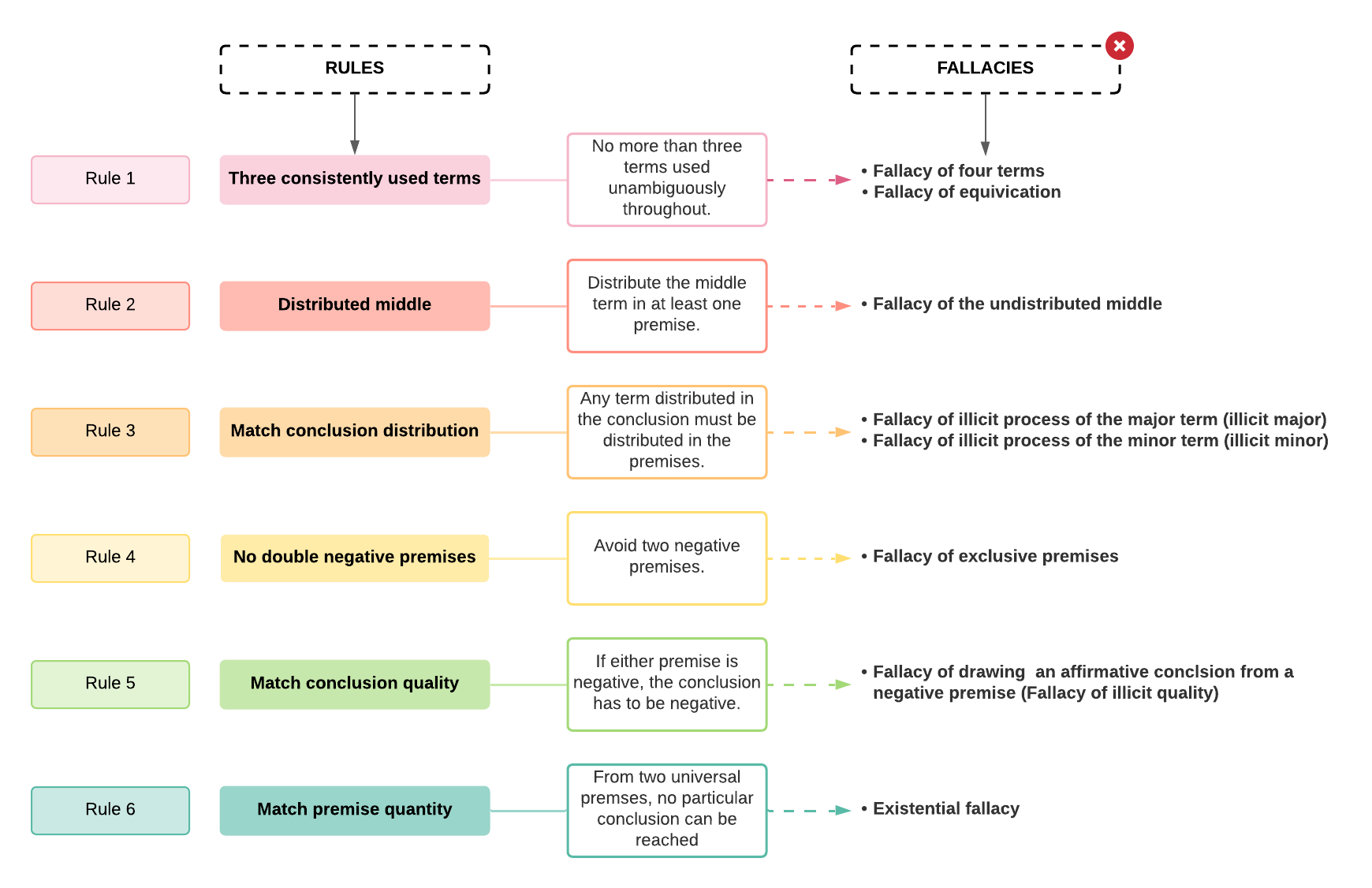
The violation of these rules results in a formal logical fallacy. Alongside each rule in the final column, you can see the name of the formal fallacy that results from violating each of these rules.
Let’s practice assessing an argument with these rules (this example is adapted from one by Ronald L. Hall at Stetson University, used under a CC BY-NC-SA 4.0 licence):[1]

Without checking any of the rules, we already know it’s invalid because if we grant the truth of the premises, they don’t force the truth of the conclusion. All three propositions are true, but the truth of the conclusion isn’t guaranteed by the premises offered. Let’s check the rules to see why it fails:
| Rule 1 A syllogism can only have three terms, and these must be used in the same sense throughout the argument. | This passes because there are three terms (‘cat’, ‘mammals’, and ‘dogs’) that are used equivalently (they refer to the same things throughout). |
| Rule 2 Distribute the middle term in at least one premise. Distributed means to make a generalisation of a whole class or category | Our syllogism passes this rule because the middle term (‘cats’) is distributed in the major premise. |
| Rule 3 Any term distributed in the conclusion must be distributed in the premises. | This isn’t violated because the major term (‘mammals’) isn’t distributed in the conclusion, and the minor term (‘dogs’) is distributed in both the conclusion and the minor premise. |
| Rule 4 Avoid two negative premises. | Our syllogism passes this rule because only one premise is negative. |
| Rule 5 If either premise is negative, the conclusion has to be negative. | This argument has failed and has committed the fallacy of illicit quality, since an affirmative conclusion is drawn from a negative premise. |
| Rule 6 From two universal premises, no particular conclusion can be reached. | Our syllogism passes this rule, since the conclusion is universal. |
Table 6.1. The Six Rules
So our example argument committed the fallacy of illicit quality, and therefore, is invalid.
Another example, which will start to feel quite familiar:

| Rule 1 A syllogism can only have three terms, and these must be used in the same sense throughout the argument. | This passes because there are three terms that are used equivalently (they refer to the same things throughout). Our three categories are: ‘people living in the city Honolulu’, ‘people living on the island Oahu’, and ‘Kanoe’. |
| Rule 2 Distribute the middle term in at least one premise. Distributed means to make a generalisation of a whole class or category | Our syllogism fails this test because the middle term or category (‘the island Oahu’) isn’t distributed in either premise. At no point is the whole class or category of ‘the island Oahu’ referred to. This term remains undistributed in both premises and so the fallacy of the undistributed middle has been committed, and our argument is invalid. |
| Rule 3 Any term distributed in the conclusion must be distributed in the premises. | This isn’t violated because the major term (‘the city Honolulu’) isn’t distributed in the conclusion and the minor term (‘Kanoe’) is distributed in both the conclusion and the minor premise. |
| Rule 4 Avoid two negative premises | Our syllogism passes this rule because no premise is negative. |
| Rule 5 If either premise is negative, the conclusion has to be negative. | Our syllogism passes this rule because no premise is negative, and the conclusion isn’t negative either. |
| Rule 6 From two universal premises, no particular conclusion can be reached. | Our syllogism passes this rule, since the conclusion is universal. This may be confusing because the conclusion is about ‘Kanoe’, and so seems particular. However, the term ‘Kanoe’ refers to the whole class or category, so is universal, rather than referring to some of ‘Kanoe’, which would make it particular. |
- Hall, R. L. (n.d.). Categorical arguments. In R. L. Hall, Logic: A brief introduction. Stetson University. https://www.stetson.edu/artsci/philosophy/media/G.%20%20Chapter%206.pdf ↵

