Chapter 4. How Knowledge is Constructed
Learning Objectives
- Understand the JTB definition or framework of knowledge
- Appreciate the distinction between belief and knowledge
- Understand the empirical basis of knowledge
- Understand the distinction between analytic and synthetic knowledge
- Appreciate the different requirements for justifying analytic versus synthetic knowledge
- Recognise the difference between a fact and a hypothesis
- Understand the difference between inductive and deductive procedures for obtaining knowledge
- Recognise the different uses of induction and deduction in science
- Appreciate the power and utility of knowledge.
New concepts to master
- Justified True Belief (JTB)
- Epistemology
- Empirical
- Analytic versus synthetic knowledge
- Fact
- Hypothesis
- Ampliative inference
- Explicative inference.
Chapter Orientation
This chapter’s content leads naturally on from the last chapter where we started talking about the nature and pitfalls of sense, perception, and beliefs. This chapter is all about knowledge, and by this point in the text, you won’t be surprised to find out that this topic comes with a host of new issues, pitfalls, complications, and surprising concerns. Last chapter we learned about our beliefs – what we believe, how we believe, and how we structure and even attempt to protect our beliefs. This chapter will focus on what we know, how we know it, when we can say we know something, so on and so forth.
Knowledge is one of the most primary and fundamental intellectual concerns of humanity. We’re emotionally motivated to acquire and hold on to beliefs that we take as knowledge. Ignorance is terrifying to us – we feel the anxiety of our lack of knowing acutely. In previous chapters, we’ve touched on the vulnerability this anxiety creates in our thinking. Because knowledge is power (more on this at the end of the chapter), and that power gives us a survival advantage, we’re hardwired through millions of years of evolution to desperately look for – and cling to – any piece of information, no matter how error-prone it is. Because of this, we fall prey to a plethora of prejudices and biases in our desperation to escape the terror of the unknown.
Definitions of knowledge date back several thousands of years, to Plato. The definition of knowledge has been the subject of a 2500-year-old war, first described by Plato in his work, The Sophist. In fact, this war of definitions was a major starting point for Western philosophy. The war Plato described is over whether there is anything that can be called ‘knowledge’ that isn’t mere belief or opinion. That is, whether it’s possible for knowledge that is universal and certain. According to the Platonic myth, the gods and earth giants were at war. The gods were on the side of the philosophers, who argued that real knowledge was possible, that there were things we ‘knew’, and that this knowledge was certain (there couldn’t be any doubt about it), necessary (this knowledge couldn’t be wrong), and universal (what was known to be true didn’t change according to the person, the place, or the time), and that these three descriptions all imply each other. The sophists and the skeptics of Plato’s day were represented in this war by the earth giants. They maintained that what we call ‘knowledge’ is uncertain (we could be wrong about it), it’s only likely (we’re only justified in having a degree of confidence in it), and it’s also context-dependent (it did change according to people, places, or times). The gods and philosophers could point to necessary, certain, and universal knowledge in the form of geometric truths and sound deductive arguments, while the earth giants and skeptics could point to the overwhelming instances of times when humans thought they had true knowledge, only to find out later they were wrong.
Just like in the history of Rugby League’s State of Origin, throughout this war, one side seemed to be on the ascendancy only to be quickly knocked back down to size. This war still rages today without any clear resolution in sight. Think about what side of the war you might be on. Do you believe there’s such a thing as knowledge that’s universal, necessary, and certain? Or do you believe everything called ‘knowledge’ is nothing more than probabilistic, contingent, and personal beliefs and opinions? In this chapter, we’re going to dive into the issues relating to knowledge and get into some of the nitty-gritty technical stuff that concerns this debate.
As you can tell, knowledge is another everyday idea that quickly becomes insanely complex once we start pulling on threads involving definition and justification. In an everyday sense, there are some things we know, and some things we don’t, right? What concerns us in learning to be critical thinkers is understanding what exactly the difference between these two states is. What does it mean to know something? And what qualifies something as known? We would all agree that just believing something isn’t enough to claim knowledge (believers in a flat earth are a testament to this). We can also say with certainty that we don’t know the things we’re wrong about. Consequently, our beginning analysis (which has only really scraped the surface), has revealed that knowledge seems to be about getting at the truth rather than mere belief.
Last chapter we spent a bit of time learning about beliefs, so this chapter will launch straight off from that point because knowledge is most commonly defined as ‘true beliefs’. This phrase ‘true beliefs’ also indicates how knowledge is a type of success term that’s usually considered distinct from mere belief or opinion. A more complete statement is that knowledge is ‘justified true belief’ (called the JTB Definition or Framework), which is a definition provided by Plato almost two and a half thousand years ago that has not yet been improved on (Plato uses the term ‘argument’ to refer to ‘justification’).

To flesh this out a bit, what I think I know only counts as knowledge if:
(1) It’s true (that’s the T)
(2) I believe it’s true (that’s the B)
(3) I’m justified in believing it (that’s the J).
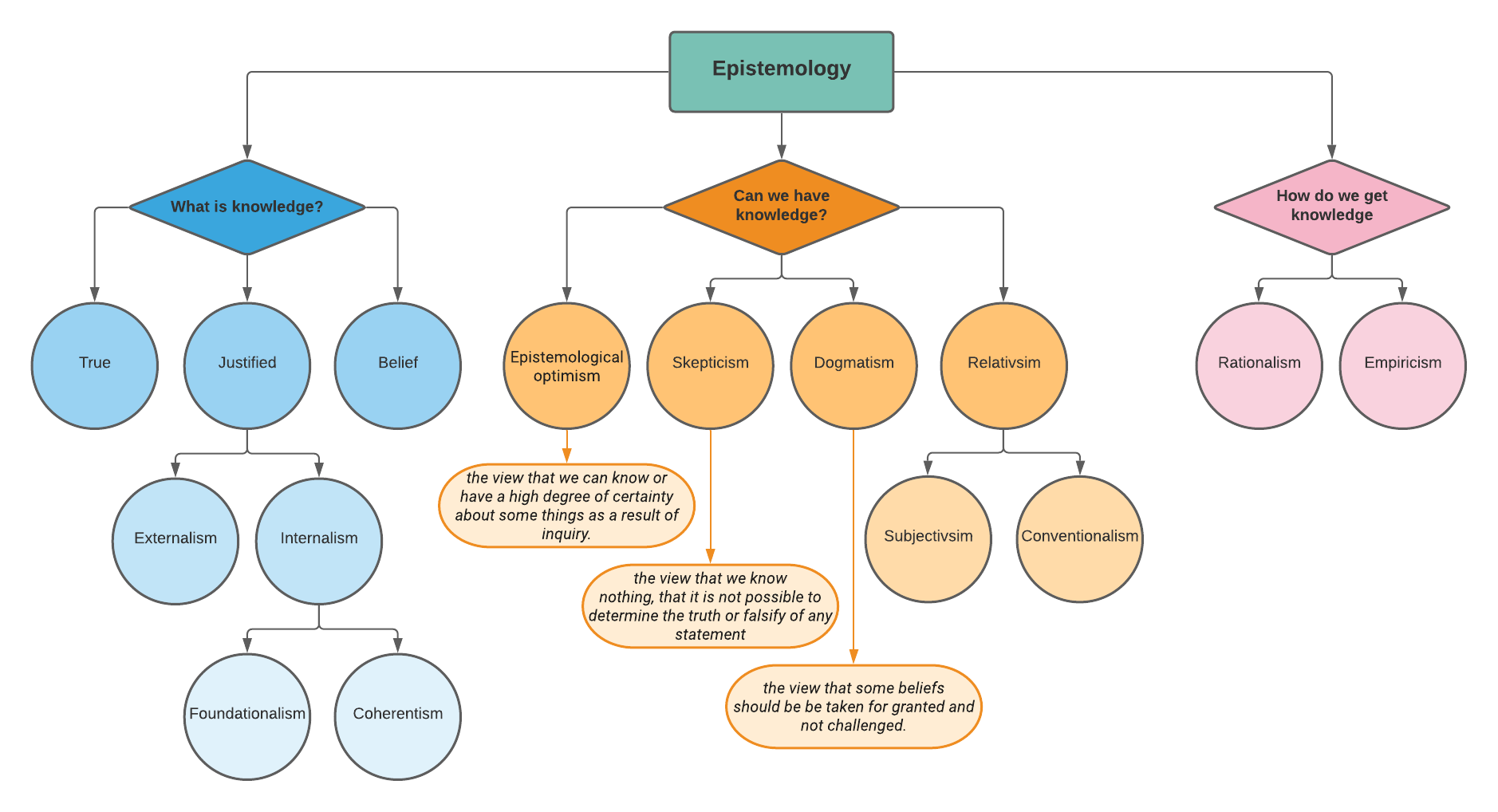
The study of knowledge is a discipline known as epistemology, and so this is our first technical term for the chapter.
‘Epistemology’: Epistemology is one of those fancy words people like to use to sound smart, so feel free to drop it into an inappropriate place in a conversation at some point. The term is a combination of two Greek words: episteme and logos. ‘Episteme’ means ‘knowledge or understanding’, whereas logos means ‘account’ or ‘argument’ or ‘reason’. Words with ‘ology’ at the end of them (like psychology or epistemology) usually mean a study or a science of something. Therefore, epistemology is the study or science of knowledge. Consequently, this chapter (and to an extent, this whole book) is really about epistemology. Epistemologists are concerned with understanding what knowledge is, how knowledge can be justified, and the limits to human knowledge.
This framework or diagram (see Figure 4.1) is a useful way to represent the relationships between some of the issues and ideas we’ve focused on for several chapters now. You can see how some of these concepts are organised, and how they relate to each other. We’ve already come across the JTB definition on the left. In the middle, we can see some of the explanations about knowledge that are on the side of the earth giants (scepticism and relativism), and we’ve already started defining some of the other terms such as empiricism.
Before we get too far into this chapter’s material, I’d like to put it in context by linking it to the last chapter, so let’s recap.
Chapter 3 Review
We started the last chapter by looking at the basics of our sense and perceptual systems. We likened them to signal detection systems which have evolved to pick up specific signals from our environment, process them by transforming them into electrical signals, and pass them on to our brain. Yet, we learned that this signal detection account of sense and perception was only half the story. There are also a lot of what we call top-down influences on our sensations and perception. Unlike some commonly-held views, our perceptual experiences are not merely a bottom-up product of raw sense stimuli. Some instances of top-down influences are observable in things like perceptual illusions, and we learnt that these types of perceptual experiences can be a helpful way of understanding that what we ‘see’ isn’t always really there, and vice versa.
We looked at one type of top-down influence on our perception that are known as heuristics. Heuristics are strategies that act as shortcuts for processing information and help us make decisions more quickly. Heuristics are tools that simplify cognitive tasks and reduce our information processing burden – we simply don’t have the computing power to get through the day without using heuristics. However, the drawback of heuristics is that they’re only rough approximating tools. We can easily see our reliance on heuristics when we come to what seem like quick and ‘good enough’ (though wrong) solutions to logical problems like the Bat-and-Ball Problem and the Lily Pad Problem.
Important for our purposes are heuristics that are known as cognitive biases, which are a set of systematic shortcuts that are useful for helping us quickly process information and make rough-and-ready decisions. These biases evolved for good reasons, but are problematic because they don’t aim to get the world ‘right’, but rather, just to increase our survival. Last chapter, I shared some links to compiled lists and diagrams that cover many of the cognitive biases you’ll encounter. I encourage you to go and study these.
Other top-down influences on our sense and perception apparatus include the influence of our psychological states. We saw that some mental illnesses serve as clear examples of top-down influences on sensation and perceptions. It turns out that perception is a creative process that emerges out of the dynamic interaction of our sense organs with our brains. All this is shaped heavily by our worldviews, belief systems, and store of concepts.
Aside from these top-down influences, we learned about some of the specific limitations of our sense organs. For example, the fact that our eyes and ears are only sensitive to a very narrow range of the possible signals that are available. Through the social media episode of #TheDress, we also saw an example of how different people with correctly operating perceptual systems might actually see very different things.
We delved into some deeper philosophical perspectives on problems in sense and perception, including Plato’s Allegory of the Cave, the distinction between primary and secondary qualities (John Locke), and the distinction between noumena and phenomena (Immanuel Kant). According to these accounts, we don’t have direct contact with the ‘thing’ in itself (which is the noumena), but perceive something like shadowy reflections cast on a wall and then imbue these perceptions with a range of (secondary) qualities that are not directly possessed by the ‘thing’ in itself (or the noumena).
In the absence of some good critical thinking, we tend to hold a naive perspective that’s often called naive realism. This is a position that holds that the objects we perceive and interact with in the outside world do really exist, and also exist exactly the same as we perceive them. We learned that naive realism wasn’t a defensible or convincing perspective. Additionally, our interaction with the world is more like an augmented virtual reality simulation, in which our brains directly influence and add to our sense experiences. We also saw some other perception illusions (like Magic Eye pictures) that illustrate this.
The second half of the chapter looked at beliefs and models. Our worldview is like an internal cognitive model or map. It’s a very powerful instrument that we use to navigate the world, to make predictions about the future, to interpret the past, and to make sense of what’s happening in the present. Models are powerful instruments precisely because they’re abstractions that retain important features of the ‘thing’ being modelled (in this case, the outside world), while eliminating many other features that are considered unimportant. Our cognitive models are an approximation we’ve built up from our own experiences and from observing others. Yet, because they’re abstractions, they discard a lot of potentially important information, and therefore, are only ever rough approximations. For this reason, we need to be careful and flexible with our models (like all our beliefs) simply because (as with heuristics) these have evolved over millions of years to maximise our survival – not necessarily to be accurate depictions of the world. And yet, we’re very heavily reliant on worldviews and models – they act as lenses which influence how we see the world and how we interact with it.
We looked at how beliefs are related to our internal working models (our internal working models are a set of beliefs). A belief is a proposition that we accept as being true. Consequently, a belief is a personal position of endorsement that we adopt towards propositions or claims about ourselves and the world. We learned about the dynamic interaction between our beliefs and sensations. Beliefs and expectations directly influence what we see and perceive – we saw this at work in Bruner and Postman’s famous anomalous playing card experiment. The problem of the direction of influence between beliefs and raw sensations started to look a bit like the old chicken-and-egg conundrum, where neither necessarily precedes the other, but they constantly influence each other cyclically. Beliefs are constantly shaping the sensation we have, which in turn influence the updating of our beliefs, which in turn shapes new sensations and perceptions.
A major drawback of strong belief systems was our natural tendency to try to maintain them through certain sneaky processes like confirmation bias. This bias is simply the universal tendency to search out, to notice, to attend to more closely, accept uncritically, and to remember information that confirms what we already believe. Our beliefs are structured to protect those that are at the core of our worldview. This core is surrounded by a protective belt of less important – and you might say, more disposable – beliefs. This allows us to safeguard beliefs that we’re very committed to from falsification. This approach to or understanding of the systematic relationship between beliefs (developed by Willard Van Orman Quine) is called holism. The take-home from this is that we should be aware of our tendency to avoid falsification of beliefs we’re very committed to, or that are core to our worldview.
We need to resist our unwillingness to falsify certain beliefs by adopting a healthier relationship with them. Some appropriate attitudes that can make us more resilient to holding erroneous beliefs include modesty. Modesty is the most appropriate disposition towards our beliefs because we simply don’t know nearly as much as we think we do, and we could be wrong about everything we currently believe. The next good attitude to develop is intellectual courage, with a focus on falsifiability. We need to be committed to falsifying our beliefs, not trying to maintain them. Evidence to confirm beliefs is cheap, and not particularly useful in getting at truth, whereas falsifying evidence is decisive. In contrast, falsification is easier and pays off more in the long run. Finally, I described openness and emotional distance as good approaches to hold towards beliefs. We should try not to become too attached to any of our beliefs. We should maintain a healthy emotional distance from them so that we don’t resist falsifying them when we come across new information. All too often we fall in love with our beliefs and then make fools of ourselves, waging unwinnable wars trying to protect them (a lot of the arguments on social media are an expression of this).
What is Knowledge?
Let’s start with the basics, which we touched on at the start of this chapter. The first thing we want to ask ourselves is, ‘What is knowledge?’. The nature of knowledge has been a central problem in philosophy from the earliest times. One of Plato’s most brilliant dialogues, the Theaetetus, is an attempt to arrive at a satisfactory definition of the concept.
As you’ve become used to by now with other philosophically loaded concepts, definitions of the term ‘knowledge’ are controversial, and there is little consensus among the so-called ‘experts’. At the beginning of this chapter, you were introduced to the classical Platonic definition (when someone says ‘Platonic’, they mean it came from the teachings of Plato) of knowledge as ‘justified true belief’ (this is called the JTB definition). All three of these conditions are necessary to satisfy a claim to knowledge. But as we’ll see, satisfying these conditions is much more difficult than you might think.
After our last chapter, we understand belief as ‘a personal position of endorsement that we adopt towards propositions or claims about the world’. The true part of the JTB formula is a more difficult one, and for a lot of knowledge, we really never know with any certainty about its truth. Also, you can see that the elements J, T, and B are rather interdependent since truth really depends on the ‘J’ in the sequence because ‘J’ is the only way we would be able to determine the ‘T’. In most cases, people would simply not believe things in the absence of ‘J’, so it’s all a bit incestuous.
The distinction between belief and knowledge is a critical one. Someone might say, ‘I don’t know how he performs that magic trick, but I believe he uses mirrors’. In this use, knowledge is a kind of success term – to know is to have achieved something that’s stronger than a belief. However, to know starts with a belief. We can’t know something if we don’t believe it. For example, if it’s a psychological fact that ‘A positive attitude towards a behaviour increases one’s chances of performing that behaviour’, but you don’t believe it to be true, you can’t be said to have this knowledge, despite the knowledge being true. Similarly, someone can’t know something that isn’t true. For example, if you believe the claim that ‘A positive attitude towards a behaviour increases one’s chances of performing that behaviour’ is actually untrue, you don’t know this – you merely have an erroneous belief. Therefore, knowledge seems to have a lot to do with truth, and to know is our endorsement of those things that are true.
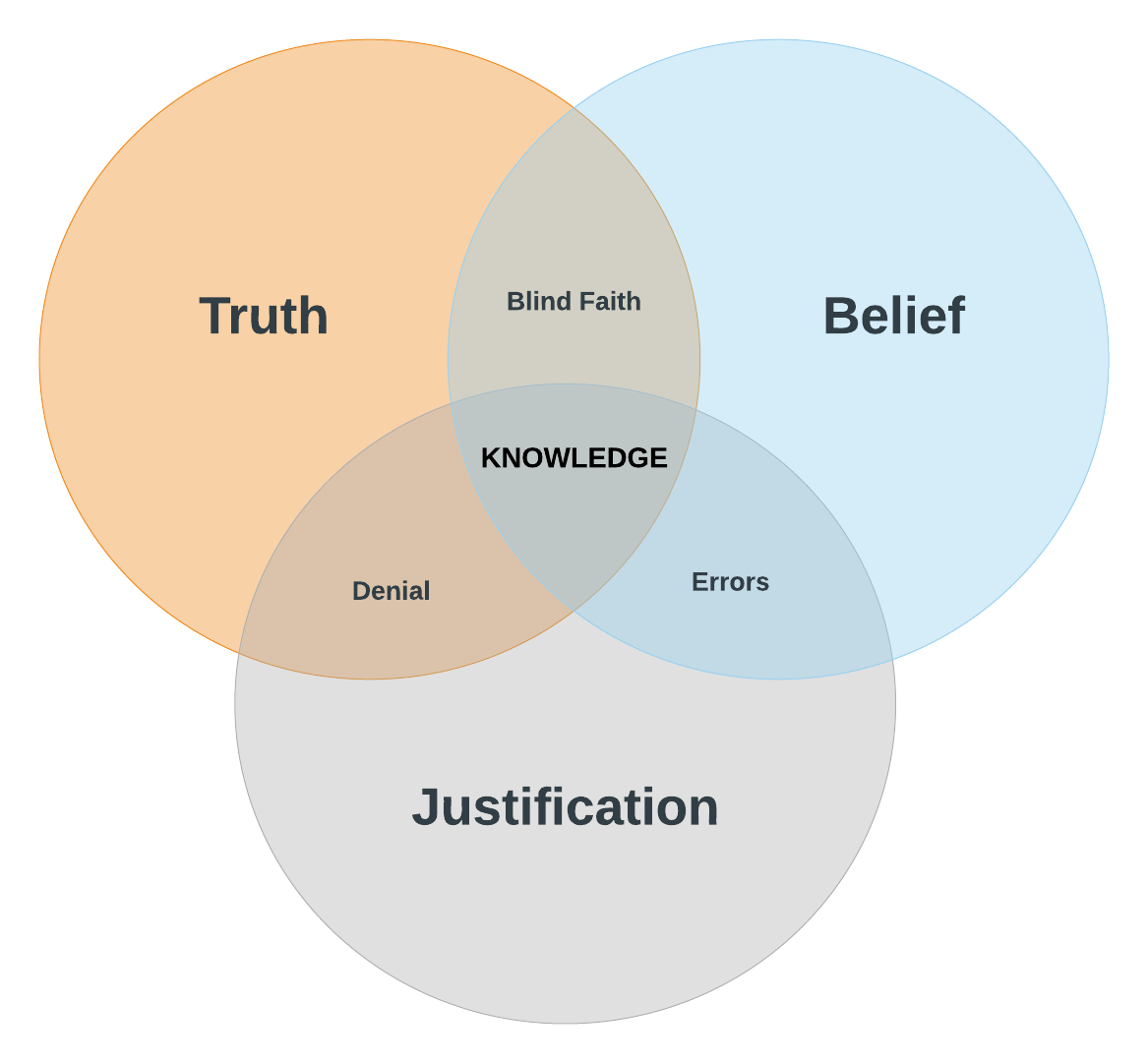
In the following diagram (see Figure 4.2), you can see the overlapping wedges corresponding to:
- Blind Faith: Unjustified belief.
- Denial: Things you should believe, but don’t.
- Errors: Things you believe, but are wrong about.
- Knowledge: Things that are true or that you believe are true, where you have good reasons for believing their truth.
By understanding the combination of truth, justification, and belief, we can begin to understand how we arrive at these different positions.
So what’s the complication? Well, the greatest challenge is the ‘J’. How do we go about justifying beliefs in order to claim knowledge? As I said in Chapter 2, a claim about the world that could be ‘knowledge’ is nothing more than a conclusion in an argument that’s sustained by specific reasons and evidence that serve as its premises. In appraisal (or step) 2 of the Theory: Developing Knowledge portion of Chapter 2, ‘Logic and argument analysis’, I outlined some elements to the appraisal of arguments. The steps to untangling the argument that serves to address the ‘J’ (justification) part of the JTB framework of knowledge should be straightforward. Finding the pieces of an argument isn’t always easy, especially in spoken arguments or debates. Firstly, we want to identify the conclusion. What is the main point? Conclusions are often easier to identify than premises. What does the argument primarily intend for you to believe? Next, we identify the premises. To identify the premises, you can ask yourself, ‘Why is this conclusion believed?’, ‘Why does this conclusion make sense?’ or ‘What is the rationale behind this conclusion?’. As I’ve said previously, if you’re dealing with a specific claim, and the premises are not made apparent or stated clearly, then you’re under no obligation to agree with the conclusion or even take the argument seriously.
For different types of claims, different types of justifications are conventionally taken as sufficient. Below (Figure 4.3) is an exercise you can complete to practice matching justifications to claims. Read through the list of knowledge claims in the centre and choose the justification (from the surrounding circles) that you think is most appropriate. (I’m not suggesting any of these justifications are sufficient to qualify the claim as ‘knowledge’ – this is just for practice.) The answers to this matching exercise will be provided at the end of the chapter.

Uses of the Term ‘Knowledge’
Like all loaded terms, ‘knowledge’ gets used in many different ways. There’s procedural – or know-how – knowledge, such as knowing how to bake a cake or replace a car battery (neither of which I know how to do, so I have no procedural knowledge about these processes). Then there’s acquaintance –or familiarity – knowledge. For example, you might know me, or you might know Brisbane, or your local town (insert whatever people and places you’re familiar with). The kind of knowledge we’ve been talking about so far in this chapter (and generally in this text) isn’t procedural or acquaintance knowledge, but rather propositional knowledge, which we’ve learned concerns a definition, fact, or state of affairs represented by a proposition.
Recall what we’ve learnt since Chapter 2: that propositions are declarative statements (or assertions) that concern a claim about the world (this repetition is intentional because I want to marry up pieces of the puzzle from all the chapters, so the story seems something like a sensible whole). There are different types of propositions and each requires a different type of justification.
Next, we’ll learn about a distinction between analytic and synthetic propositions. Synthetic propositions are propositions we’re likely to confront in everyday life – particularly in science. Those of you studying science subjects such as psychology will find that most of the propositions you’re dealing with are synthetic propositions. If you’re studying mathematics or logic, most of the propositions and types of justification you’ll be dealing with are analytic. Given that most of the propositions and justifications dealt with in psychology studies (and all health sciences) are empirical, we should stop to define this term.
‘Empirical’: The term empirical refers to sense experiences. What you observe through your senses qualifies as empirical evidence. Scientific methods rely almost exclusively on empirical evidence or direct observation of the world. Whenever you hear the word empirical, you should think observation (though observation here is used loosely and includes all sense data – not just visible data). Therefore, empirical evidence is evidence someone has collected by going out in to the world and examining specimens, surveying people, watching behaviour, etc. Empirical justification refers to using sense experience to support propositions – as opposed to rational justification, which relies on concepts and theories (e.g. analytic justification).
Knowledge is generally considered to be more than empirical information. Knowledge is arrived at by a combination of theoretical and empirical inputs. These two can’t get very far without the other. Specifically, the flood of disorganised sense experiences that bombard us have to be processed, understood, and made sense of by rational thought. Likewise, rational thought must be fed by, ‘tethered to’, and ‘checked by’ sense experience, or it may fly off into a wild fancy and produce only useless beliefs. Our friend Immanuel Kant put it best when he said, ‘All our knowledge begins with the senses, proceeds then to the understanding, and ends with reason. There is nothing higher than reason ’.[1]According to Kant, our minds impose structure and meaning onto raw sense experience in order for it to be intelligible to us. Kant also explains the necessity of sense (empirical) and thought (concept and theory) working in unison: ‘Thoughts without content are empty, intuitions without concepts are blind… The understanding can intuit nothing, the senses can think nothing. Only through their union can knowledge arise’.[2]
Analytic and Synthetic Knowledge
When it comes to propositional knowledge, historically there were considered to be two broad types: analytic and synthetic knowledge (the types of ideas that can be represented in analytic and synthetic propositions). This is distinction – referred to as Hume’s Fork (Figure 4.4).– was first popularised by Scottish philosopher, David Hume.
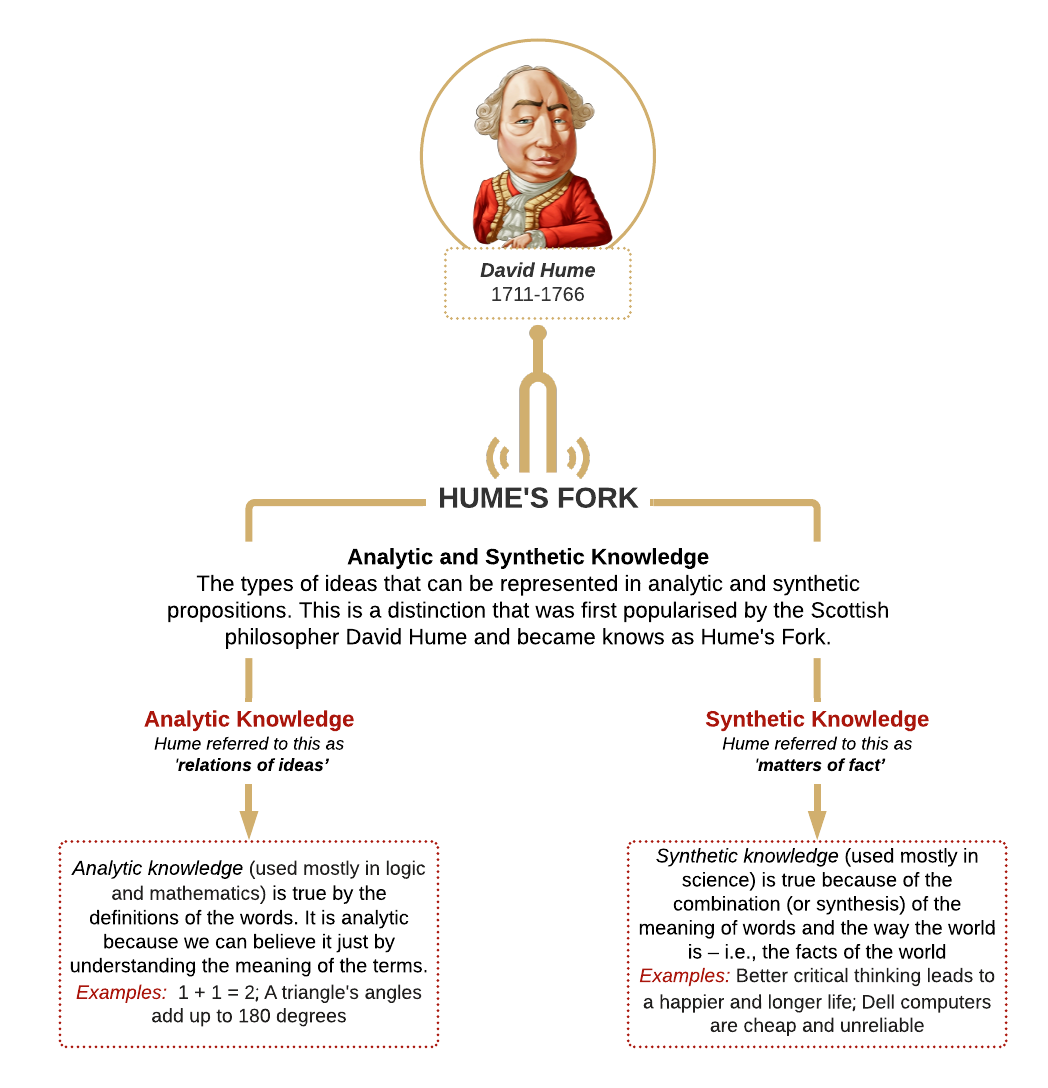
Analytic knowledge (what Hume called ‘relations of ideas’) is true by definitions of the words. It’s analytic because we can believe this type of claim just by understanding the meaning of the terms. Analytic truths can be known by reason alone. Synthetic knowledge (what Hume called ‘matters of fact’) is true because of the combination (or synthesis) of the meaning of words and the way the world is – i.e. the facts of the world. So analytic knowledge comes from the meaning of the words we use and the ideas we have, whereas synthetic knowledge comes from both the meaning of the words and the nature of the world itself – for this reason, synthetic knowledge is almost always empirical. Analytic truths don’t tell us much about the world. The reason this is relevant here is that it concerns the types of justification required for these types of propositions.
‘Analytic versus Synthetic knowledge’: Statements about the world (i.e., propositions) often fall into two main categories: analytic and synthetic. We’ll cover a third category, normative statements, later on. Here’s the difference between the first two:
- Analytic Statements: These are true simply because of the meanings of the words used. They’re like self-defining puzzles; the answer is built right into the question. For instance, “All bachelors are unmarried” is true just because of what “bachelor” means – it’s the definition of the word.
- Synthetic Statements: These are claims about the real world, true because of what we observe or experience, not just word definitions. They’re called synthetic because they synthesise (combine) information from both the meaning of the words and empirical observations. Think of the statement, “The sun rises in the east.” This is true because we see it happen, not because the word “sun” means “rises in the east.” Synthetic statements are like scientific discoveries; they require evidence to prove them.
To remember this, think of analytic statements like maths problems you solve using logic and word meanings, while synthetic statements are like science experiments, needing real-world proof.
A quick grammar note: Every claim has a subject (the thing being discussed) and a predicate (what’s being said about it). In the “bachelor” example, “bachelors” is the subject and “unmarried” is the predicate. Here are a couple of other examples:
- “Dogs are loyal companions.” (Subject: dogs; Predicate: loyal companions)
- “The sky is blue.” (Subject: the sky; Predicate: is blue)
As you can see, the subject is typically a noun or noun phrase, while the predicate is a verb or verb phrase that describes or modifies the subject. Understanding this basic structure of claims can help you break down and analyse propositions and is also crucial to determining the validity of whole arguments like categorical syllogisms, which we will discuss later.
Don’t worry if the grammar seems a bit tricky at first. You can understand the big picture of analytic and synthetic claims without getting bogged down in the details. The key is to recognise the difference between claims that are true by definition and those that require evidence from the world around us.
This distinction matters mostly in deciding what types of justification are needed for different statements. Analytic claims don’t require justification using external evidence, just clear definitions of the terms. A prototypical analytic claim like ‘Triangles have three sides’ illustrates this.
If you understand the definition of ‘triangle’ (literally ‘three angles’), then the fact that they have three sides is undeniable – it’s a necessary and certain truth because the concept of ‘three sides’ is inherent to the very definition of a triangle. Like all analytic propositions, the predicate (having three sides) is a part of the subject (being a triangle). Synthetic claims require both clear definitions of the terms (because any claim needs this) and external evidence to support them as premises. I’ll illustrate with some more examples.
Analytic propositions are statements like ‘Ophthalmologists are doctors’, which counts as knowledge because it’s true just owing to the meaning of the word ‘ophthalmologist’. The subject term ‘ophthalmologists’ implies the predicate – that we’re talking about a doctor specialising in eye disorders (of course this might vary according to national context, but in Australia, it’s true). However, a synthetic statement like ‘Ophthalmologists are rich’[3] might count as knowledge only if it turns out to be true that ophthalmologists earn lots of money (though we would still need to know what ‘rich’ means here before we could count this claim as knowledge – the meaning of words is always primary and critical). Consequently, for analytic truths, you don’t need to know anything more than the meaning of the terms in the proposition, and we don’t need to go looking for evidence to serve as premises for such claims or conclusions. The important thing to consider when deciding whether an analytic proposition counts as knowledge or not, is whether the statement is meaningful and coherent. More examples will help.
A claim like ‘Snow is white’ is synthetic because it’s a claim about something out in the world, not just a claim about the meaning of terms. For a statement like this, we would want to go out and actually see some snow to test it. And snow isn’t always white– it’s often yellow because people like to pee in it. Prototypically, analytic statements like ‘All bachelors are unmarried’ or ‘All triangles have three sides’, are clearly true without having to know anything about the world outside or having to do any experiments. For this reason, a proposition like ‘All mammals give birth to live young’ is analytic, precisely because giving birth to live young is a defining feature of being a mammal. If we did go out and do some research and find something that’s supposed to be a mammal that only lays eggs to procreate, then we don’t reject the proposition (‘All mammals give birth to live young’), but rather, we must revise our classification of this particular animal as a mammal or create a potentially new category for it.[4] Consequently, in this way, analytic statements aren’t dependent on external evidence, and by the same token, are unlikely to be falsified or supported by external evidence.
Think about the following propositions and decide if they’re analytic or synthetic:
- Frozen water is ice.
- Children wear hats.
- My computer is on.
- Two halves make up a whole.
- The table in the kitchen is round.
This organisation of knowledge into analytic and synthetic is a useful way to think about the truth of propositions and what the criteria of justification would be for each. However, we shouldn’t be too rigid in our commitment to this distinction. The hero of our last chapter, Quine, doubted the reality of the distinction and presented some good arguments as to why it isn’t necessarily valid. Since the very meaning of our words is built up out of experience (synthetic) and the meaning of evidence is entirely dependent on the meaning of terms (analytic), we need to be aware that conceptual category distinctions like this are always just models that we should use when useful, but not reify (more on this next chapter). I want to be honest and say that sometimes people have good reasons for disagreeing with the frameworks I introduce to you, but we don’t need to go into that here – it’s the nature of complex intellectual debates.
Let’s pause for a moment and study a brief concept map (Figure 4.5) to review what we’ve learned so far in this text about types of statements and propositions.
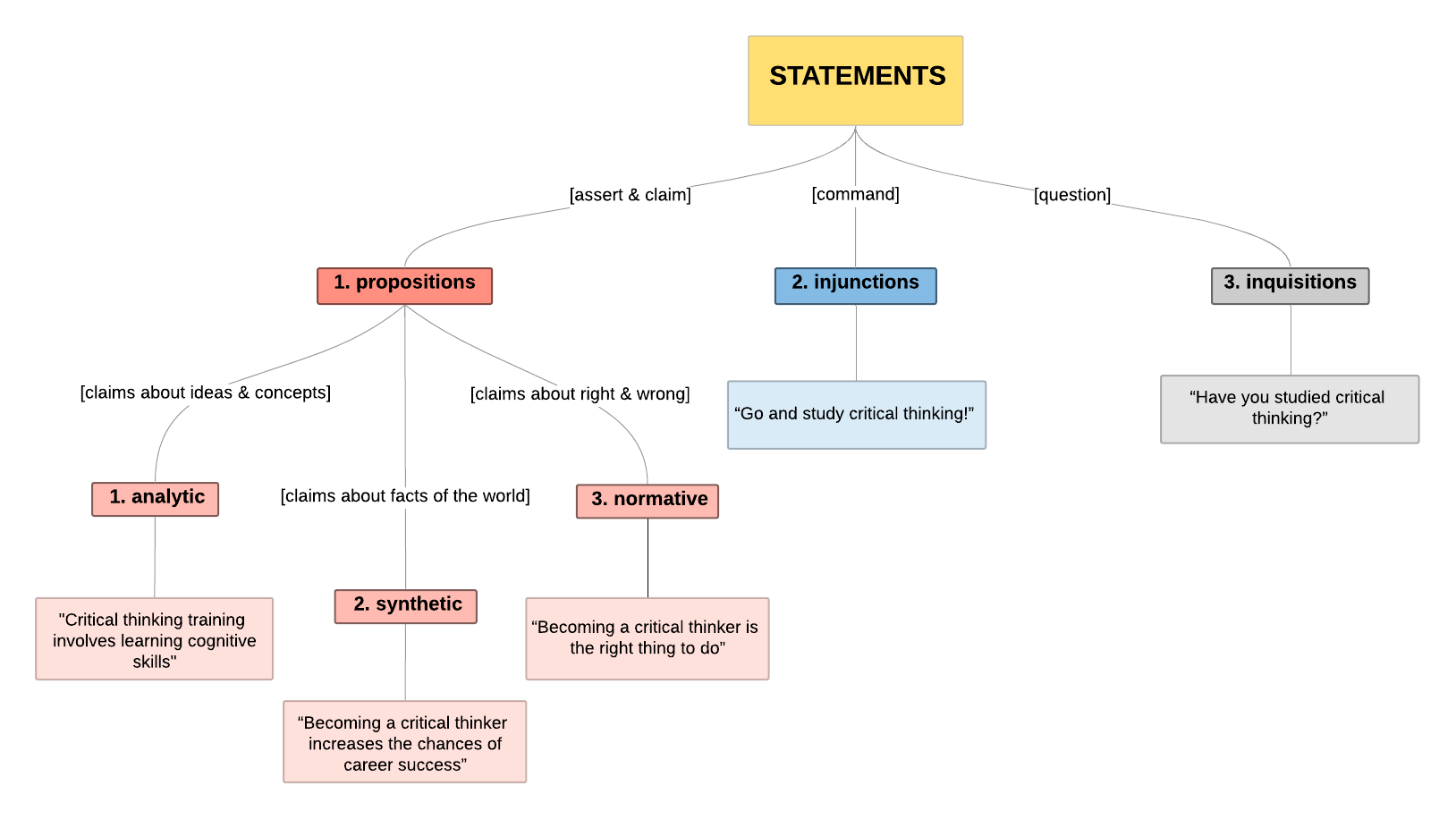
Forms and Problems of Justification
We’ve been looking specifically at analytic and synthetic propositions, precisely because these are the sorts of claims about the world we have to confront in our daily life as critical thinkers (normative propositions also concern us, but we have a whole chapter devoted to them – Chapter 8). We need to know what types of justification are suited to each proposition type so we can critically appraise these claims as conclusions and the types of premises that are offered to support them.
Earlier, I explained that it’s the ‘J’ in the JTB formula that’s the real fly in the ointment. The problems of justification have obsessed more thinkers throughout history than just about any other intellectual concern. Knowledge is the real goal in all our enquiries and investigations. But due to problems of justification, we regularly fall short of it and settle for belief as a second best.
As we saw above, different types of knowledge are often met with different types of justification. Synthetic knowledge rests on empirical evidence, and therefore, must be supported by empirical statements as premises. Consequently, if the conclusion to an argument is synthetic, you need to see some empirical evidence in the premises for that argument to be convincing. If the conclusion of an argument is analytic, you can get by with explaining definitions as the premises. Therefore, analytic conclusions can be supported purely by analytic premises, and synthetic conclusions should be supported by both analytic and empirical statements.
In this way, analytic justification is more straightforward (and actually possible) – we observe this in fields that have ‘proofs’ such as mathematics and logic. Take, for example, ‘truths’ of arithmetic or geometry. These are reasoned out from the basis of premises that are taken to be self-evident or analytically true. In this way, true claims (called theorems) are derived from a small set of simple axioms or assumptions (e.g. ‘Things which are equal to the same thing are also equal to one another’, which is a self-evidenced axiom we can use as a premise to arrive at analytic truths or conclusions). In this way, analytic sciences like geometry don’t require empirical or outside justification, but are true on the basis of reasoning alone. An easy example of this is the proposition that ‘2+2=4’, which is true just owing to the definition of the term ‘2’ and the operation ‘+’. We don’t need to know anything more than what ‘2’ and ‘+’ mean to know that 2+2=4. If we did do some empirical calculation and found 2+2 didn’t =4, we wouldn’t think of that proposition as falsified because it’s analytic – it doesn’t get falsified by observation. Instead, we would have committed some sort of miscount or have done our calculations wrong. In this way, these types of propositions meet the criteria of Plato’s gods and achieve knowledge that’s universal, necessary, and certain.
Epistemologists and scientists would like to develop similarly conclusive methods for synthetic propositions, but unfortunately, this Holy Grail of philosophy and science has alluded them. Despite many efforts, no one has been able to come up with a convincing solution to the problem of how we can have universal, necessary, and certain knowledge of synthetic propositions. Essentially, synthetic propositions require empirical evidence for justification, and as we’ve seen, the procedures for justifying propositions with empirical evidence are fraught with challenges such as the vulnerability of scientific methods to bias, the fickleness of inductive conclusions, the overall inclusiveness of confirming evidence, and all the problems with sense and perception that we dealt with in the last chapter.
Facts and Knowledge
Facts are propositions or statements about the world that we take to be true. Therefore, the designation ‘fact’ is like a qualification of a proposition. When a proposition is believed to have sufficient justification (even if we just set aside the headaches that securing justification brings), it graduates to the status of ‘fact’. A fact is a proposition in the same way a belief is, however, it’s called a fact because there’s enough evidence available to make it very unlikely a reasonable person would reject it. Facts are often thought of as propositions that are well or easily verified in a way that means they can reliably be taken for granted (but in this text we’ve learnt nothing can really be taken for granted). In this way, propositions that are false or that are not yet justified are not considered factual. Consequently, there is no such thing as ‘alternative facts’, despite what US Trump administration Senior Counselor to the President, Kellyanne Conway, claims.
‘Fact’: A fact is something that’s the case – that is, a state of affairs – that has been provided with sufficient justification to earn the title ‘fact’. Similar to when you have enough justification of your own study at university, you’ll earn the title ‘psychologist’. We take propositions to be ‘factual’ when we’re convinced by the justification. There is some subjectivity here, however – it isn’t a personal judgement (we can’t all have our own facts). Rather the judgement about ‘factfulness’ follows objectively stated procedures for justification and is usually a decision at the community level (a community of scientists might accept something as a fact – even if it then turns out to be incorrect, it’s still a fact because it met minimal and accepted standards of justification).
Any proposition we believe is a viable candidate for being a fact, but if it hasn’t yet received any justification, we might call it a ‘hypothesis’ or a ‘conjecture’. Therefore, hypotheses are fact candidates that haven’t yet undergone procedures for their justification. So, let’s get clear on this term as well.
‘Hypothesis’: As with most of the key terms in this book, the word hypothesis has meant many different things throughout its history. There are times in the history of science when the word hypothesis was a derogatory word – even Isaac Newton has a famous quote, ‘I do not feign hypotheses’ as a bit of a slap in the face of Galileo, who came up with all sorts of hypotheses about how mechanics worked. However, these days, hypothesis isn’t a derogatory term. For most people today, a hypothesis is a testable claim about the world. More formally, Barnhart (1953) describes a hypothesis as a single proposition proposed as a possible explanation for the occurrence of some phenomena.[5]. Not all hypotheses are scientific, but in order to be considered a scientific hypothesis, the proposition must be either analytically (by virtue of logic and meaning) or empirically (by virtue of observation) falsifiable. If you come across a research paper where the author claims to have hypotheses, but you can see they’re not written in a way that could be falsified by observations, then these are not scientific hypotheses.
Facts are, so to speak, the raw material or building blocks of knowledge, but it’s generally agreed that there is more to knowledge than facts. We covered this above when we looked at other types of knowledge, such as procedural or acquaintance knowledge.
Creating Knowledge
This chapter isn’t called ‘Theory of Knowledge’, but rather, ‘How Knowledge is Constructed’, so let’s move on to the constructing part. The question that concerns us here is: How do we come to ‘know’ anything? Where does our knowledge come from?
Deductive and Inductive Knowledge
Let’s once again look at inductive and deductive procedures for generating knowledge. I can already hear those sighs and groans, and you are saying, ‘No, not more logic!’, but I’m sorry to say we’ll lean on logic to some extent in all our chapters. This is intentional because you’re learning a new skill – a new way of thinking – and logic is as important to a thinker as a scalpel is to a surgeon.
We’ve already learned about deductive and inductive reasoning, but we’ll understand them a little more deeply now with respect to the type of knowledge they each can offer us. It was Aristotle (who we met in Chapter 1) who, without any predecessors, basically invented logic almost single-handedly. He established the rules of reasoning that would give us certain knowledge. He argued that certain knowledge was a conclusion (a truth) that was derived from other known truths (premises).
 Deductive and inductive reasoning are two ways of arriving at knowledge using premises (reasons and evidence). Now, while it’s true to say that by definition ‘knowledge’ is something about which we have to be certain, we rarely meet this high ideal. Consequently, we need to make room for knowledge or ‘truth’ that’s less than certain, but still useful (recall our discussion of approximating models and worldviews in our last chapter). Therefore, we can make room for the earth giants and think of knowledge in a more nuanced way – to see it operating more on a continuum, rather than a hard-lined ‘true or false’ type dichotomy. In this way, we make room for inductive or non-certain knowledge.
Deductive and inductive reasoning are two ways of arriving at knowledge using premises (reasons and evidence). Now, while it’s true to say that by definition ‘knowledge’ is something about which we have to be certain, we rarely meet this high ideal. Consequently, we need to make room for knowledge or ‘truth’ that’s less than certain, but still useful (recall our discussion of approximating models and worldviews in our last chapter). Therefore, we can make room for the earth giants and think of knowledge in a more nuanced way – to see it operating more on a continuum, rather than a hard-lined ‘true or false’ type dichotomy. In this way, we make room for inductive or non-certain knowledge.
Let’s consider five possible gradations or degrees on a continuum of knowledge (see Figure 4.6), starting with ‘certain’, then ‘probable’, then ‘plausible’, then ‘possible’ then ‘unlikely’. It could end with a ‘false’ or ‘untrue’ category, but we don’t really need that point on a ‘knowledge continuum, as it’s the opposite of knowledge. Thinking along these lines can help us understand the role and power of deductive versus inductive reasoning a little bit better.
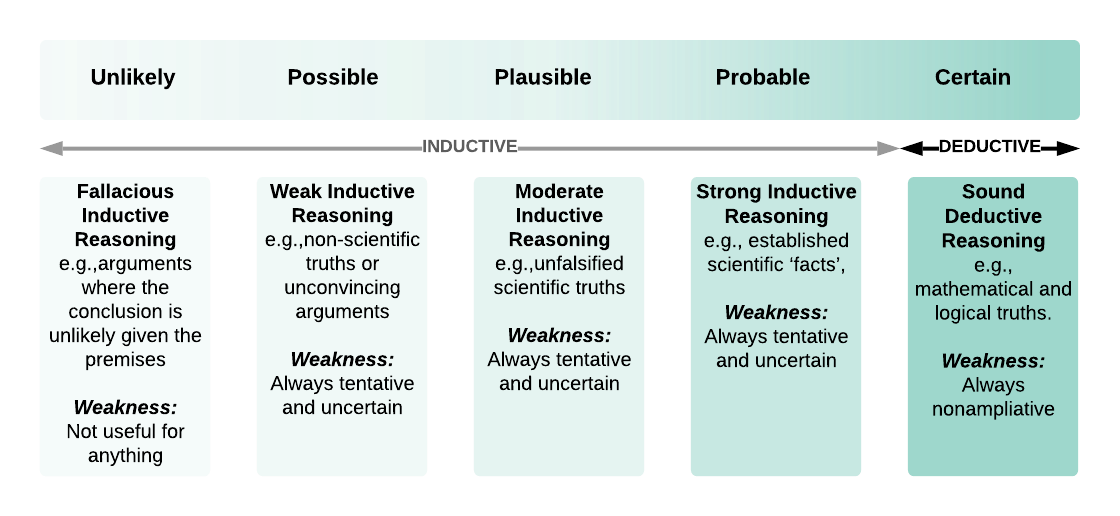
Of course, we always aim for as much certainty as possible when it comes to knowledge, and only sound deductive reasoning can offer us this. Remember from Chapter 2 that it’s the structure of the deductive argument and its soundness (recall that soundness means having true premises and a valid inference) that guarantees certainty. Therefore, in a sound deductive argument, the conclusion is ‘certain’ and beyond doubt (so Plato’s gods would approve). However, the weakness of deductive arguments is that they can’t provide us with new knowledge that goes beyond the premises. For this reason, they’re not ampliative. We call this type of argument explicative. You can already anticipate what will be our next technical term.
‘Ampliative’ and ‘Explicative’: Ampliative is a term you’re unlikely to have heard before. It’s a term used in logic, and it just means extending or adding to what is already known (it has the same Latin roots as ‘amplify’). Reasoning is ampliative if we can go beyond the information presented in the premises to entirely new information. Induction in this way can be said to be ampliative since it does allow us to arrive at new facts on the basis of specific premises. Sometimes inductive reasoning is even called ampliative reasoning as a way of distinguishing it from deductive reasoning. Therefore, if you’re doing some Google searching to learn more about inductive and deductive reasoning, and you see descriptions of ampliative reasoning, they’re just talking about inductive reasoning.
In contrast to ampliative induction, explicative is the term often used to describe deductive reasoning, which is nonampliative because the conclusion of a deductive argument doesn’t really say anything new that wasn’t already contained in the premises. Think of the following deductive argument:
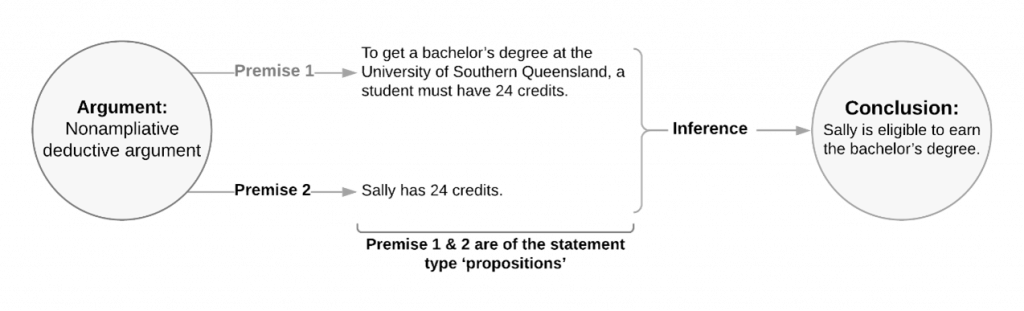
This isn’t really new knowledge if we already had these premises on hand. This argument is therefore nonampliative because the conclusion doesn’t give us new knowledge, it’s merely an extension or explication of the premises (explication here means teasing out the implications of a definition). Therefore, deductive reasoning is purely explicative reasoning, which means it just explicates or teases out the implications of what we already know or the meanings of words.
Explanation Sidebar: ‘Deduction and Induction’
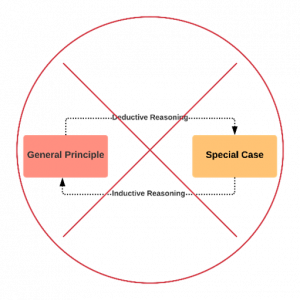
If you google the difference between induction and deduction (as well as look it up in many non-logic textbooks), you might find people saying that deduction is a reasoning pattern that goes from the general to the specific and conversely, that induction is a reasoning pattern that goes from the specific to the general. Well, this is a simplification, which is misleading. To the right there’s an example illustration:
It’s true that deduction is often used to identify specific implications from general principles (like deriving an observational hypothesis from a theoretical proposition), and it’s also true that a series of specific instances can be used to inductively reason out a general principle behind them (a type of generalising induction). But these are not to be taken as representative patterns of deduction and induction. It’s just as legitimate, and common, to deduce a universal proposition (general principle) as a conclusion in a valid deductive argument. Likewise, it’s legitimate and very common to reason to a specific instance as a conclusion to an inductive argument (for example in predictive or analogous inductive arguments).
For example,
Universal Premise: All dogs are mammals.
Particular Premise: Fido is a dog.
Singular Conclusion: Therefore, Fido is a mammal.
and
Universal Premise: All birds have feathers.
Particular Premise: Some animals are birds.
Particular Conclusion: Therefore, some animals have feathers.
These arguments are both valid deductive syllogisms
Below is a graphic (Figure 4.9). that links together some of the ideas we’ve covered so far in this chapter (analytic versus synthetic, deductive vs inductive, ampliative versus explicative), as well as ideas from previous chapters.
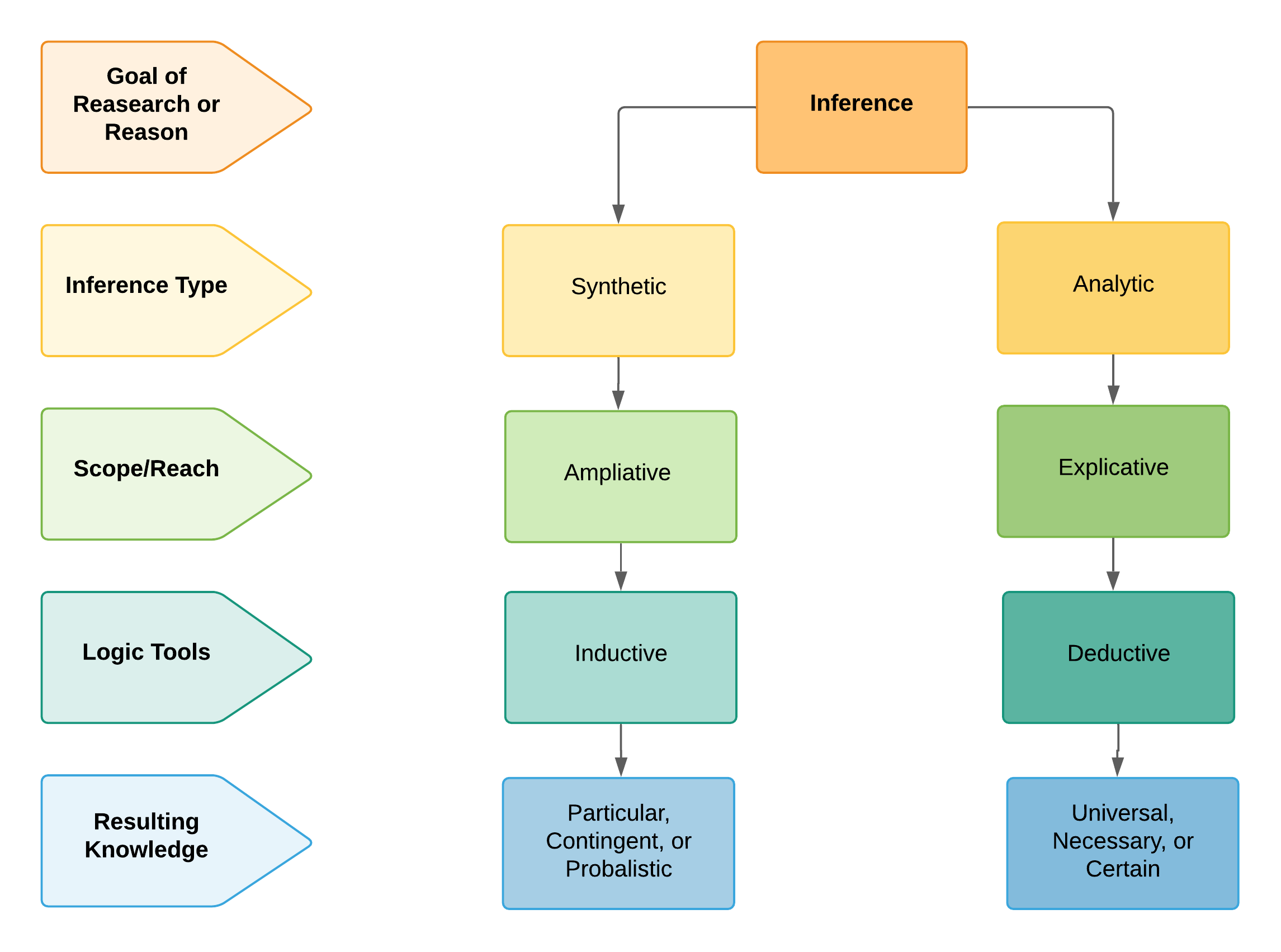
We can see the goal of research or reasoning is inference. We have two main types of knowledge we can infer. Note that the scope of the knowledge isn’t the same: Synthetic claims of knowledge are ampliative and try to go beyond the premises to new information, and therefore, are more likely to rely on inductive reasoning. Analytic claims are explicative and try to explicate or tease out the implications of certain terms without going beyond them, and therefore, are more likely to rely on deductive reasoning. Lastly, in the final row, you can see the resulting knowledge that emerges from these two pathways.
We now know that the knowledge provided by the conclusion of a sound deductive argument is certain (providing the premises are true, and the inference is a valid one) and that it achieves this certainty by being restrained in its reach – that is, it’s explicative rather than ampliative. Nevertheless, don’t think that deduction isn’t useful in learning about the world. It’s exceptionally powerful in allowing us to explicate (or tease out) the consequences of the definitions and knowledge we already have. For example, take the premises that (a) All dolphins are mammals, and (b) All mammals have kidneys. Though the conclusion that ‘All dolphins have kidneys’ might have been buried in the premises, it doesn’t mean it was always apparent. The power of deduction is to extract facts from premises by explicating their meaning and implication. A mathematical example might have as its premise: ‘All numbers ending in 0 or 5 are divisible by 5’. With this premise in hand, if someone asks, ‘Is 35 is divisible by 5?’, you can deduce that it is without having to do any calculating. Someone might ask, ‘Can cacti perform photosynthesis?’. You might not know this specific fact, but you can arrive at it fairly quickly if you know – and reason – from the following two premises: (1) ‘Cacti are plants’, and (2) ‘All plants perform photosynthesis’. So, while you may not have reasoned it through before, you could have worked out at any time that cacti do, in fact, perform photosynthesis. What you’re doing is explication, or working out new knowledge from what is already known.
Inductive knowledge is ampliative, and by trading off the certainty of deduction, it allows us to venture into unknown territory armed with our accumulating specific premises. In inductive reasoning, we progress in knowledge by picking up new reasons and evidence to serve as premises, just like a player picks up new weapons in a first-person shooter game. The problem is, we could always be wrong about the knowledge we draw from our inductive adventures, yet for most of the things we want to know about, we don’t really have much choice. Consequently, on ‘the knowledge continuum’ (Figure 4.6), we can see that inductive reasoning provides us with either possible, plausible, or probable knowledge depending on the strength of the evidence that forms the premises. The word ‘probable’ here is customarily used when talking about inducting, but it is actually a bit misleading. The probability here is more of a subjective sense of certainty that we take from strong inductive arguments, not an actual objective probability (if you’re more statistically minded, you might think of it as closer to a Bayesian probability). That is to say, a stronger inductive argument doesn’t have more probability of being right – it just seems that way to us.
Good inductive reasoning provides us with knowledge that’s more or less convincing. The more accumulated evidence and reasons we can uncover, the more convincing the truth of the knowledge gets – but it never leaps the great gulf into certainty. This hard boundary between convincing and certain knowledge can’t ever be overcome. That inductive arguments never yield certain conclusions is similar to the natural law that nothing can go faster than the speed of light – it’s simply a fixed impossibility. Countless embarrassed scientists have learned this lesson the hard way over the centuries.
Deduction and Induction in Science
As you might have gathered, mathematics and logic studies rely heavily on deductive reasoning. Scientists also use deduction, for two different things:
- deriving hypotheses (observational consequences) from theoretical propositions
- falsifying propositions using disconfirming evidence.
Regarding the first use, if there’s a theory that, ‘People with low self-esteem will also suffer from more depression’, I could deduce that a consequence of this premise being true is that individual scores on self-esteem and depression instruments should be correlated (it’s a valid deduction because if the premise is true, the conclusion has to be true). I can then collect data to see if this is actually the case. The second use relates to what we do with propositions once evidence comes in. The reason falsification in testing of scientific theories is so powerful is because it relies only on deductive logic. Let’s look at one of the examples from above:
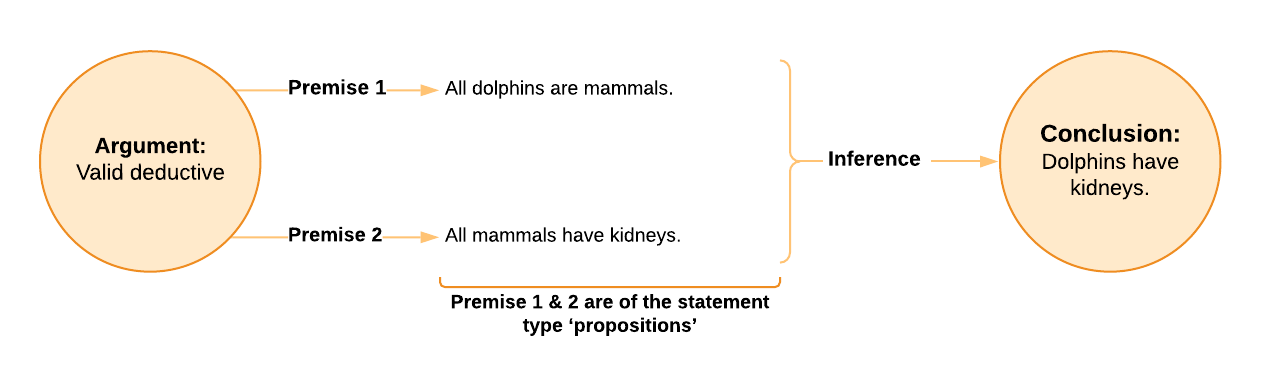
We start testing our conclusion by working out what would be an observational consequence of it (which, is what we generally call a hypothesis). Remember, a scientific hypothesis is an empirically falsifiable observational (it has to appeal to empirical data) consequence of a theoretical proposition. In our example, the hypothesis could be that, ‘If we dissect dolphins, we should find kidneys’. If, however, after performing our horrifying experiment, we can’t find any kidneys in the dolphins, we can deductively conclude: (1) the inference leading to that inference is invalid, or (2) that one of the premises is false. According to deductive reasoning, when a conclusion is false, it’s either because the premises are false, or because the inference is invalid. In this case, the inference is fine. Remember To check the validity of an inference, simply ask yourself: If the premises are true (don’t worry if they’re not, this is just for the sake of argument), does the conclusion absolutely have to be true as well (is it inescapable and necessary?). In this example, this is satisfied. That means, if, for the purpose of testing the inference, we just accept the premises on blind faith, we shouldn’t have any choice but to accept the conclusion, so the inference is a valid one. And yet, according to our gruesome experiment, we actually have a false conclusion. Therefore, if the observational consequence shows our conclusion to be false, we can’t blame the inference (because it’s a valid one), so we know one or more of our premises have been falsified. If the proposition that is the hypothesis derived deductively as an observational consequence of a theoretical proposition turns out to be false, either the inference was invalid or one or more premises are false.
However, finding a true conclusion (or supporting a hypothesis) doesn’t have the same type of decisive power. For example, a conclusion can be true, and yet the premises can still be false. This is a little difficult to grasp, I know, but providing the inference is valid, true premises can’t create a false conclusion – however, a conclusion can still be true even if it has false premises and a sound inference. False premises can lead to either a true or a false conclusion, even in a valid argument. It’s a false conclusion that immediately signals either an invalid argument or untrue premises. Let’s borrow an example:
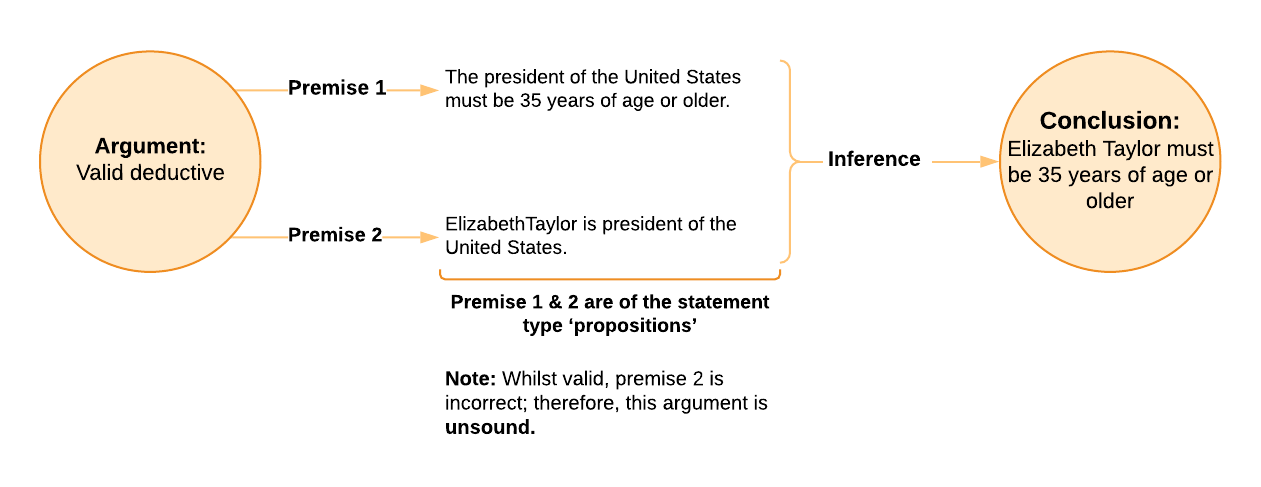
Whenever we’re analysing an argument, our first check is to determine if the inference is valid, and we check this by deciding whether the premises, if we grant them as true, would force the conclusion to be true. For our example here, this criterion is passed, so it’s a valid deductive argument – but that isn’t to say it’s all fine and dandy. Next, we inspect the premises for their truthfulness. I don’t actually know if the first premise is true (seems odd, but might be true), but I do know that the second premise is definitely rubbish, and yet the conclusion is actually true. Consequently, we can have something of an accidentally true conclusion, which is possible even when the premises are false, and the inference is valid. This is because the truth of the premises doesn’t rely on the truth of the conclusion, it’s only the reverse that’s true. Remember I said in Chapter 2, that the truthfulness or falseness of the premises relies on their own arguments. Therefore, determining whether the premises themselves are true or not is a separate analysis, and usually a matter of analysing the arguments where these very premises serve as conclusions (in our example here, I know premise two is untrue because it’s self-evidently false). So, we know that this argument isn’t sound (remember that soundness means both that the premises are true, and the inference is valid), however, because the conclusion is true, we can’t use it to falsify any of the premises. In contrast, when the conclusion is actually false, something has gone wrong with either: (1) the premises, or (2) the inferential move from the premises to the conclusion. So, here we have an example of an argument where a true conclusion doesn’t give us a lot of help in uncovering false claims (untrue premises) and progressing our knowledge. Conversely, a false conclusion would have been much more helpful in rooting out false premises or bad (invalid) inferences.
Let’s look at an example of a fairly commonplace pattern of inductive reasoning that most parents will be familiar with:
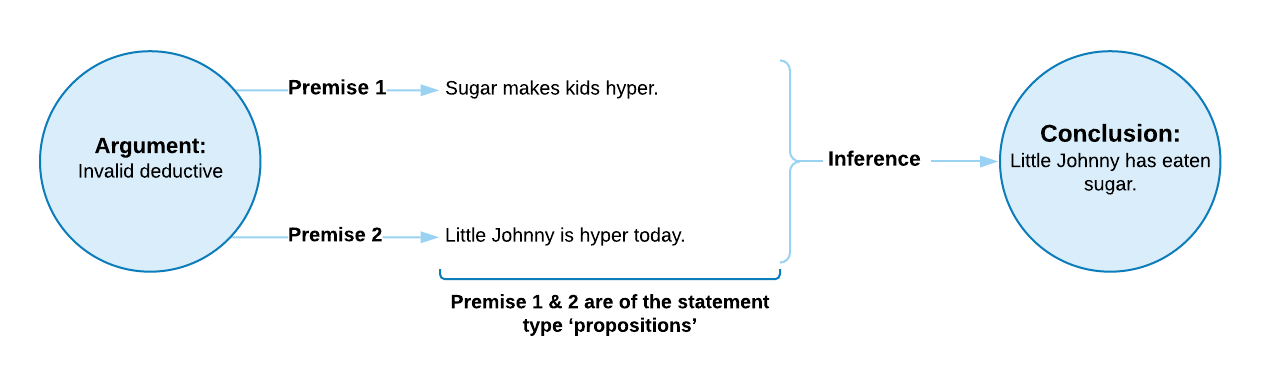
Once again, the first thing we want to do is to check if the inference is valid. In this case, the inference isn’t strictly valid because the premises could be true, and yet they don’t force the conclusion to be true. Both of those premises might be true, and Johnny hasn’t had any sugar today – maybe he just snorted a bunch of cocaine instead. Consequently, we don’t have a valid deductive argument. Instead, we have an inductive argument, which means we’re inheriting a host of vulnerabilities that inductive reasoning is exposed to (the inferences are very insecure in these arguments).
Lo and behold, Johnny’s mother checks this hypothesis or conclusion by thinking back to what he has eaten today and remembers that he ate a sugary cereal that morning. Therefore, this is an argument with a true conclusion. If the conclusion was false (he hadn’t had any sugar that day), we could use our airtight deductive reasoning to work backwards from the false conclusion to knowing that one of the premises must be wrong (or the inference is wrong, as we saw in the case of Johnny having a secret cocaine habit). If we suspect the premises – not the inference – to be at fault here, and we’re looking directly at hyper little Johnny, it’s likely the first premise that bears the blame.
Once again, if the conclusion does check out, it can’t really be taken as evidence that the premises are true, since a true conclusion is no guarantee that the premises given for it are true. And in actuality, sugar doesn’t make kids hyper, though this myth just won’t seem to die.[6] This is a common belief among parents who fall prey to faulty inductive thinking because they see a constant conjunction between sugar-eating and hyperactive behaviour, and draw this faulty type of inductive conclusion.
Therefore, because we have a true conclusion, we might think this argument does give some support (confirmation) to the premises, even though we know the first premise is false. This is a good example of how confirmation is cheap and unreliable. Whereas with falsification, in cases where we find a conclusion to be false, and providing the inference is valid, we know there is a false premise in the argument.
It doesn’t mean the observation that Johnny has eaten sugar and is now hyper provides no reason for believing the claim ‘Sugar makes kids hyper’. To make this work, we need to turn it into a much stronger inductive argument (remember, unlike deductive arguments which – when sound – are always airtight, inductive arguments can always be more or less convincing, or more or less strong). Here, we could strengthen this inductive argument by adding more reasons and observations (evidence) to serve as premises.
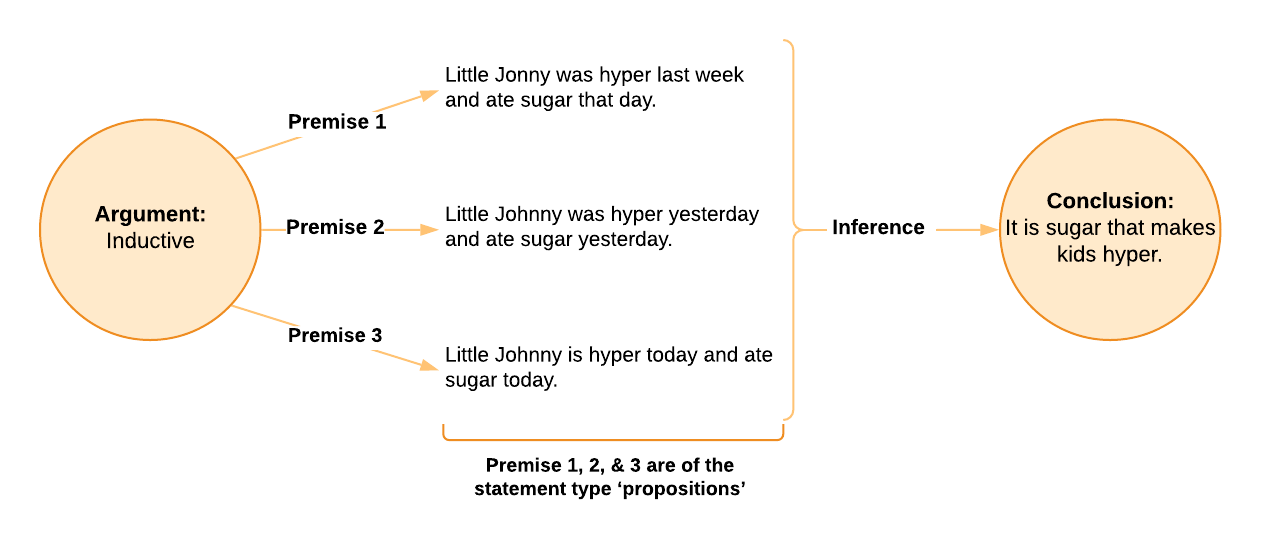
Once again, we have a good illustrative example (we’ll learn in Chapter 6, this is a generalising type of induction) because the conclusion remains false. We know scientifically that sugar doesn’t make kids hyper (neither does food colouring, or preservatives, or artificial flavours, however, if you get your facts from shows like Today Tonight or A Current Affair, you might still believe some of those things). As before, we know it’s inductive since it’s formally invalid as a deductive argument because the conclusion isn’t guaranteed even if the premises are true – it commits the formal logical fallacy of the non sequitur. As an inductive argument, the conclusion is only made more convincing by these premises (as in, with each premise we add, and each new piece of evidence we observe, we might become slightly more convinced about the conclusion). Remember from last chapter, confirmation of hypotheses is weak and inductive, while falsification is decisive and deductive.
In Chapter 6, we’ll learn how to use the specific logical procedures (the Modus Ponens and Modus Tollens) that will reveal the logic (and fallacies) behind deductive falsification and inductive confirmation. For the purpose of this chapter, remember how you determine if an argument is sound, which arguments are inductive and deductive, and what both forms of argumentation have as their strengths and weaknesses.
The Utility of Knowledge
Given all the issues raised above about how to secure knowledge, you might be forgiven for asking, ‘Why bother’? or ‘What is there to gain?’. Well, the intellectual struggle to settle the problem of knowledge and justification will result in the Holy Grail of all intellectual pursuits: ‘power’! Yep, scientists are just as power-hungry as anyone else. Keep in mind, knowledge is power – mere belief is only ever accidentally useful. And yet, we rarely have sufficient justification to call our beliefs ‘knowledge’. Quite a bind! But scientists are nothing if not audacious, and we have an almost delusional faith in our tools to uncover knowledge.
The old saying ‘Knowledge is power’ has been attributed to Francis Bacon, a one-time corrupt judge, and later in life, an influential philosopher of science, as well as a social reformer. He foresaw the power that knowledge and science would afford those who used these tools properly, and he anticipated that scientific industry and advancement would be the keys to a flourishing society and international dominance for his home country, England.

Influential historian Will Durant [7], in his recounting of Bacon’s philosophy, put it nicely by stating that knowledge that does not provide practical benefits is pointless and ‘unworthy of humankind’. Therefore, our motivation for learning is not merely for the sake of the learning itself. Rather, we seek knowledge in order to influence and reshape the world around us.
In this way, Bacon’s view is a thoroughly instrumentalist or pragmatic view of knowledge and history has shown he was quite justified and perhaps even understated it. He also favoured empirical knowledge and induction (it was not until later that thinkers – mostly David Hume – pointed out that induction cannot produce anything like justified knowledge).
Return to the Battlefront
We started out in this chapter by describing a 2,500-year-old war between the gods and earth giants over the very meaning and possibility of knowledge. After this chapter, you can see that both sides are well-armed with strong points and good evidence to support their position. It turns out that the gods and philosophers are right about the possibility of knowledge that’s universal, necessary, and certain, but this knowledge is only relating to our own ideas and analytic truths that depend on our language and definitions. Claims about the outside world or synthetic truths are, therefore, always unavoidably uncertain, more or less probable, and context-dependent.
Additional Resources

By scanning the QR code below or going to this YouTube channel, you can access a playlist of videos on critical thinking. Take the time to watch and think carefully about their content.
Answers to matching claims to types of knowledge

- Kant, I. (2003). Critique of pure reason (M. Weigelt, Trans.). Penguin Classics. (Original work published 1781) ↵
- Kant, I. (2003). Critique of pure reason (M. Weigelt, Trans.). Penguin Classics. (Original work published 1781) ↵
- These examples are from the Stanford Encyclopedia of Philosophy. ↵
- Note that the platypus doesn’t falsify this proposition since the proposition isn’t ‘only mammals give birth to live young’. Just that ‘all mammals do.’ ↵
- Barnhart, C. E. (Ed.) (1953). The American college dictionary. Harper & Brothers. ↵
- This has been known since the 1980s. https://www.sciencedirect.com/science/article/abs/pii/0272735886900346 ↵
- Story of Philosophy - Page 172 ↵

