Chapter 2, Part A. Critical Thinking in Depth: Stages, Steps, and Dispositions
Learning Objectives
- Distinguish between propositions and other types of statements
- Understand argument structures and the different role of propositions (as premises and conclusions)
- Distinguish between inductive and deductive arguments
- Appreciate the difference between types of premises (i.e. empirical, rational, definitional, etc.)
- Know the five main steps of theory (developing knowledge)
- Understand the centrality of appraisals in critical thinking
- Appreciate the importance of clear definitions in order to get started in thinking
- Understand the power of inference
- Appraise arguments for validity
- Appraise arguments for soundness.
New concepts to master
- Proposition
- Premise
- Conclusion
- Argument
- Empirical Premise
- Rational Premise
- Definitional Premise
- Inductive logic
- Deductive logic
- Non-sequitur
- Appraisal
- Semantics
- Fallacy
- Rhetorical
- Inference
- Validity
- Sound.
Introduction
As the title implies, Chapter 2 will be mostly a ‘deep dive’ into the information provided in Chapter 1. We’ll go into much more detail and get a bit more technical as well. Chapter 1 was intentionally an inoffensive and surface-level look at some of the basics in order to lull you into a false sense of security. This chapter is so dense and jam-packed with new concepts and techniques for critical thinking that I had to split it into two parts. Chapter 2 is still intended to be introductory, though, and we’ll race through a bunch of topics that will have their own dedicated chapters later in this book. Take a deep breath, go slowly, and remember – this chapter has to end sometime!
Chapter 1 Review (and Intro to Propositions and Arguments)
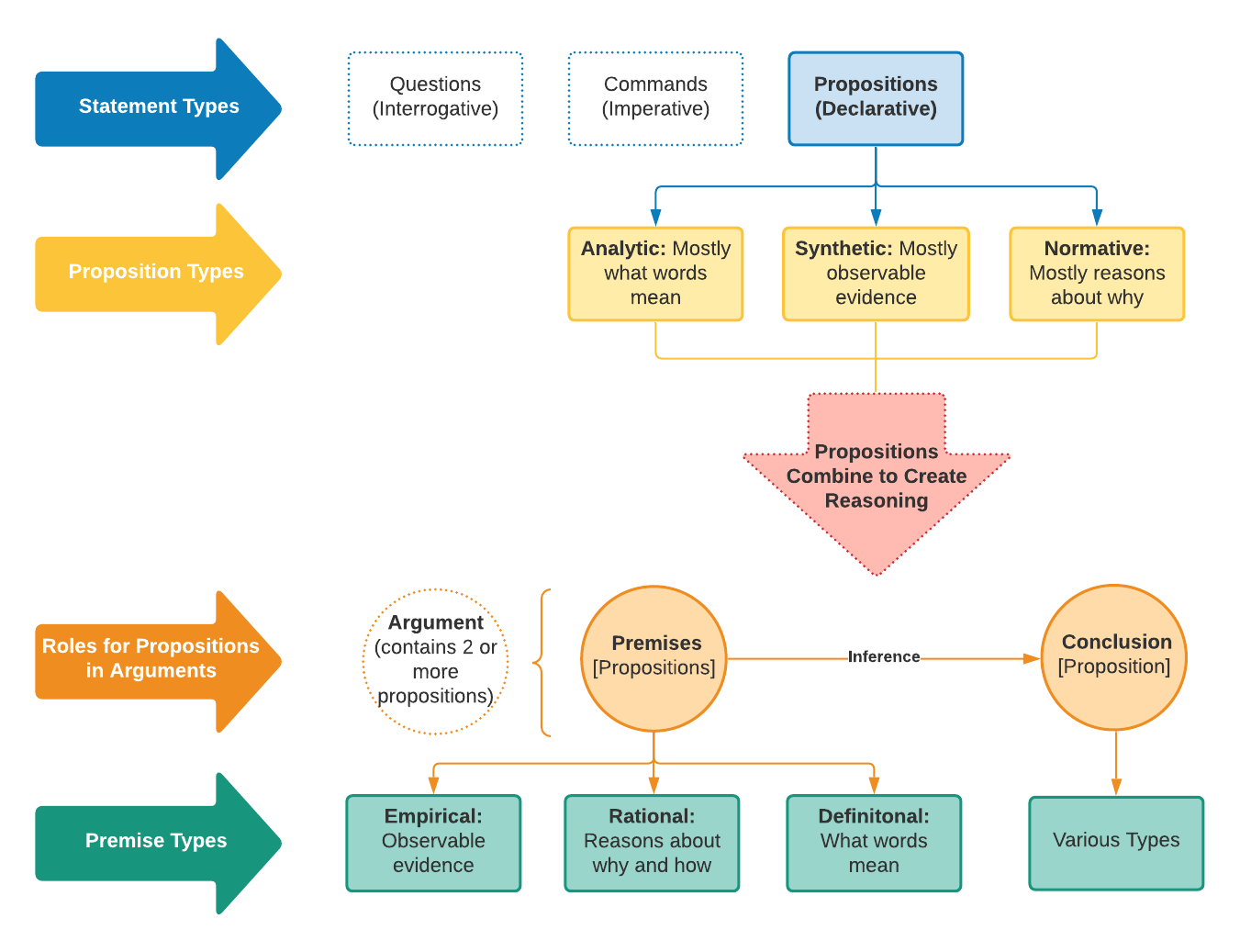
Because last chapter’s material was rather surface-level and elementary, I don’t believe it will require an enormous amount of revision. Therefore, I’ll structure this revision section in a way that introduces you to some new – and absolutely fundamental – concepts in critical thinking. The graph you see just below (Figure 2.1.) summarises much of this new content.
In the last chapter, I structured the content around a series of questions. In this chapter, I’ll present it in a new way – as a formal argument. Chapter 1 laid out several premises or reasons that serve as the basis for the ‘Whys?’ and ‘Hows?’ of learning critical thinking. Let’s take a detour into some definitions before proceeding. Remember, these are concepts that are vital to improving your thinking. Concepts are the tools you use to think and are the vocabulary in which your thinking happens. If you don’t have these concepts, you can’t think very well. To understand what a premise is, what a conclusion is, what inference is, about arguments and validity is akin to gaining a black belt in thinking, so try not to rush over this more ‘technical’ and possibly even ‘boring’ conceptual stuff. Every time you learn a new concept, you have a new thinking skill in your arsenal. And the more powerful a thinker you can become, the better your life will be.
Technical Terms Box: From here on, whenever I use a technical term that you need to understand – i.e. other content in this book depends on the term and/or it might be examinable – I’ll explicitly introduce it to you in this type of orange box.
Unfortunately, we have a bunch to get through in a row here because to fully get a handle on the term ‘premise’, we’ll need to define a few other technical terms (most of these will follow us throughout the text). As with all intellectually honest discussions, clarifying our definitions is a necessary – though sometimes boring and tedious – first step.
‘Premise’ is a formal term meaning something like a reason. Premises are declarative statements (i.e. declaring sentences) or propositions (in other words, proposing sentences) that form the basis for believing or concluding something. For example, the fact that I’m now getting wet as I stand outside can serve as a premise to support the conclusion that it’s raining. In this example, both statements – ‘I’m getting wet’ and ‘It’s raining’ – are propositions or declarative statements about the way the world is, but each has a different job. The job of the first – ‘I’m getting wet’ – is to serve as a reason to believe the second – ‘It’s raining’. This means the first proposition is playing the role of a premise, and the second proposition is playing the role of a conclusion. Not all propositions are premises, though. For a proposition to be a premise, it must be offered in support of another proposition (a conclusion). We’ll see more about this relationship in the next Technical Term Box. When a proposition is being offered in support of another proposition, then (and only then) does it qualify as a premise.
A ‘proposition’ (a ‘declarative statement’) is a sentence that expresses or asserts some claim about something that can be true or false. In most cases, many people use the terms ‘declarative statement’, ‘proposition’, or just ‘statement’ interchangeably.
Critical thinking is all about knowing what to believe, what we know, what is true and reasonable, and what is worthwhile. The types of statements that express or summarise our beliefs and knowledge are called propositions (as opposed to other statements we have in our language that ask questions or give directions). For this reason, this text is going to deal with propositions a lot and skip past other types of statements. Don’t progress past this section until you’re certain you understand what a proposition is and why it’s so important to critical thinking.
Language is the means by which we accomplish almost everything in our lives (Chapter 5 goes into much more detail about this). The pieces of our language that we use to embody and express our thoughts, beliefs, and knowledge are called propositions. Therefore, it’s essential, if we’re going to become expert critical thinkers, that we understand these types of statements, their function, how to critical evaluate them, and how they’re used in reasoning (i.e. arguments).
The distinguishing feature of a proposition – in contrast to other types of statements – is that they can be ‘true’ or ‘false’. Questions and commands aren’t the types of statements that can be true or false – we use them in our language to accomplish something else.
We’ve seen in the ‘Premise’ Technical Term Box above that propositions can be used in a bunch of different ways, such as serving in the role of either premises or conclusions in arguments. To continue the previous example, stating/claiming that ‘I’m getting wet’ is a proposition since it states a fact that can be true or false. I propose or declare that I’m getting wet. The truth of the matter is something we can check. If this claim is true, the proposition can serve as a premise or starting point with which to build an argument that supports another proposition –called a ‘conclusion’ – such as ‘It’s raining’. In this way, conclusions, just like premises, are also propositions or declarative statements whose truth depends on the truth of the premises offered. Organising sentences this way with premises and a conclusion is called an ‘argument’.
An ‘argument’ is a group or a family of sentences or statements. It’s a piece of reasoning or a chunk of reasoning. Reasoning itself can be defined as ‘the use of some information (called premises) to work out other not yet know information (called conclusions), by way of an inference’.
In an argument, one or more sentences serve as premises or reasons, and one of the sentences is the conclusion. An argument must have at least two statements, but often has many more.[1] One statement by itself can’t be a complete argument. These statements must relate to each other in this way of ‘reason and conclusion’. If the two propositions don’t relate to each other, they’re not an argument. Convincing others of the conclusion is the whole reason for the argument. You can’t have a belief without a reason – or at least, you shouldn’t! In the same way, you can’t have a conclusion without a premise. The sentences of an argument are all ‘propositions’ or ‘declarative statements’; however, they have different jobs to perform in this argument structure. The job of the premises is to support or justify the conclusion. A single argument can only have one conclusion, but it can have many premises. In an argument, premises are believed or assumed to be true. This doesn’t mean they’re guaranteed to be true – just that they aren’t justified inside the argument itself. There are most likely other arguments that justify the premises (in these arguments, those premises would be the conclusion).
Of course, it’s the job of the premises to back up the conclusion, but they don’t always succeed. Deciding how convincing premises are and how credibly they link with the conclusion are the key tasks in analysing arguments.
At the risk of being repetitive, let’s reiterate some of the important pieces of the puzzle we’ve learned so far. All statements in an argument are propositions, so they could be true or false. Every proposition rests on an argument for its veracity and believability. So, for any proposition (including those offered as premises) to be believed, they must have a strong argument to support them. Importantly, the purpose of any given argument is only to prove its conclusion – not the propositions that serve as its premise. This idea has to do with what the actual argument is attempting to prove. Premises presumably have their own arguments to support them. Each argument is only intended to support or persuade an audience about its single conclusion. Justifying its premises is not the point of an argument. Rather, premises – if they’re to be believed – have to serve as conclusions in their own arguments, which will then have different premises, like an infinite cycle. Any given argument offers premises that are meant to stand alone as self-evident or believable, or which have been justified by different arguments. Therefore, within an argument, premises are often simply assumed or offered as self-evident. When they can’t be assumed or are not self-evident, the arguer can offer separate arguments to convince the audience of the truth of the premises (or often just leave it to the audience to evaluate them).
The reason all this is important is because our thinking is a verbal activity, which means it’s done using words (we discussed concepts being the vocabulary of your thinking earlier in this book). While we also use emotions and mental imagery in our thinking, it’s predominantly all about words. However, we don’t just think in single words, but our thinking and our communication are assembled into sentences or statements. Therefore, mastering thinking and communicating requires an understanding of statements. While there is a range of different statements, the type that are the most relevant for reasoning and critical thinking are called propositions (see the ‘Propositions’ Technical Term Box above for a complete definition). Propositions are the building blocks of our reasoning, and are indispensable to understanding the world we live in. The truth of propositions boils down to arguments (see the ‘Arguments’ Technical Term Box above), which are groups of propositions in which some perform either supporting roles – as with a premise – or are the star of the show – as with a conclusion.
To summarise, we’re concerned with a particular type of statement called propositions, which are declarative or assertive sentences about something being true or not. Other types of statements are interrogative – which are about asking questions – and imperative – which are about giving directions or making requests. Propositions are often grouped because, in order to provide justification for a proposition (called a conclusion), other propositions (premises) are needed as back-up. There are several types of propositions, which we will go into more later (i.e. synthetic, analytic, and normative). We now know that within arguments, propositions have different jobs to do. Those propositions that are offered to support a conclusion are called premises. Premises can be about the nature of things (rational premises), evidence from observations (empirical premises, including scientific evidence), and definitions about what specific terms mean (definitional premises). Sometimes interrogative and imperative statements are used in arguments – though they’re not very convincing and tend to be more informal or casual (i.e. asking a rhetorical question to your friend in order to show them you were right about something).
Explanation Sidebar: Students often struggle with the distinction between empirical and rational propositions that serve as premises. A premise that focuses on reasoning proposes something about the ‘Why?’ and ‘How?’ of things, but does so without appealing to observable evidence. Premises that appeal to evidence refer to actual observations of the things being discussed. We can think of evidence as simply observing something consistent with a proposition. Taken together, a reason is an explanation about why something is true, whereas evidence is some observation that shows it’s true.
I thought a topical example might help. Let’s take the effectiveness of wearing face masks as an example. Someone arguing for the enforcement of face masks might offer an empirical premise that appeals to some evidence from scientific studies showing that communities where mask-wearing is enforced experience lower COVID-19 transmission and infection. (This is a fictitious example – I don’t know if such studies exist). Someone – presumably scientists – has made these observations (which is to say collected data on this), so it’s an empirical premise.
In contrast, a rational premise against enforcement of face masks might appeal to the nature of the COVID-19 virus being such tiny particles that the weave of the mask fabric provides no defence whatsoever (like trying to stop a swarm of mosquitos with a chicken-wire fence). Someone might counter this rational claim with another rational claim by explaining that the virus particles spread in clumps like droplets, and it’s these that the face mask provides an effective barrier to.
Here you can see that the rational claims usually appeal to the nature of things, and less directly with actual observations that have been made. The distinction can sometimes be confusing, though, as you might think that the arguments about the size of the COVID-19 droplets is presumably an observation that someone has made at some point. Yet, it isn’t these observations directly being referred to, but using the knowledge that has been gained from them to reason out something (about the ability of the face mask weave to stop the virus particles).
This outline of arguments and their structure might seem a little too abstract and intellectual to really help in daily life. But that’s only until you realise that every claim, belief, proposition, scientific fact, or piece of marketing you’re exposed to is, in reality, nothing more than an implicit (which means unstated) argument. Almost any belief can – and should – be formulated in terms of a full argument. In fact, reasoning itself is nothing more than combining propositions to form arguments and dissecting arguments to appraise the credibility of propositions.
All day, every day, we’re confronted with claims and ideas about the way the world is. For example:
- Bitcoin values will plummet in the next 12 months.
- Systematic racism is a real and devastating force in modern Western societies.
- Our sports team will win the grand final.
- The global climate is warming because of human activity.
- My political party’s candidate will make the best president.
- Our new product will prevent baldness, insomnia, wrinkles, erectile dysfunction, ageing, and so on ad infinitum.
- My birthday party this year will be spectacular.
- Critical thinking is a worthwhile course of study to pursue.
One of the most powerful critical thinking skills you can develop is to be able to unpack claims like these (which are all propositions) in terms of the argument structure that supports them. That is to say, the ability to analyse their premises and conclusions to determine whether the premises are true and just how well they support the conclusion.
Let’s illustrate with a fairly uncontroversial example proposition.
Proposition (or claim or belief): The lecturer is a nerd.
This is a proposition because it’s a claim about something. It’s a proposal or declaration that something is true, or that something is the case. However, one statement sitting all alone like this isn’t very convincing. There are no reasons to believe it, so it would normally be ignored. If I want to justify this proposition, I need other propositions to reinforce it. These other propositions are called premises. Therefore, the claim or belief I want to support is always my conclusion, and if I want it to be believed, I need to include some premises that can back it up. This then forms an argument.
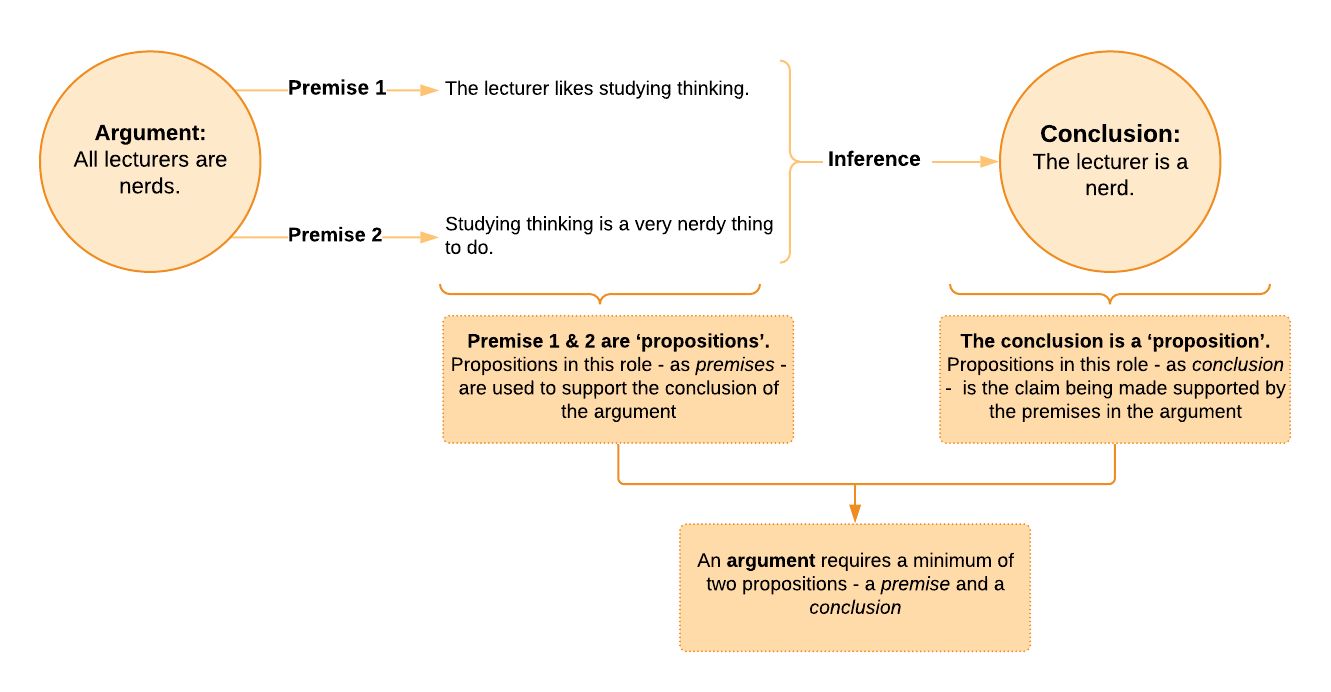
Here I offer two premises in service of convincing you of my conclusion. The first premise might be an empirical proposition because it might be based on observable evidence – that is, it might be readily observable that the lecturer is often studying thinking, or we ask him, and he confirms it, which is also evidence (we can go look at and verify this proposition). The second premise is more rational or even definitional since it isn’t something we can readily go and observe (i.e. not empirical), but it’s about the nature of something (i.e. studying) and claiming that this thing has a certain characteristic in that it’s a ‘nerdy’ thing to do.
The propositions that serve as the premises here could also be conclusions in different arguments, and have their own premises or reasons for believing them. The premises could also be reasons to support a different conclusion. However, we must examine an argument ‘as a whole’.
As I have said, these key technical terms will follow you throughout the book, so invest some time in familiarising yourself with them now. While it’s never too early to introduce you to the key concepts of our story, I’m definitely getting ahead of the narrative by outlining these technical terms. It is, after all, only the second chapter, and later on, there will be a whole chapter dedicated to dissecting arguments into their constituent statements involving premises and conclusions. However, I want to introduce you to these notions now so I can get you familiar to them by using them to summarise the content from Chapter 1. And, who knows, these terms may show up in an exam at some point.
To reorient you to our main storyline, we started out with the principle (or premise) that the brain is an unbelievably skilful, almost miraculous piece of machinery, but we’re simply handed it without any instructions or guidance on how to use it – it kind of has a mind of its own (pardon the pun). Consequently, in a sense, one way to think of this book is as a type of instructional manual for thinking or for operating your brain to maximise its potential.
One of the main reasons (or premises) motivating our desire to learn critical thinking is that this dastardly brain of ours doesn’t automatically function optimally. That’s to say, in a way that’s likely to get close to the truth. This is the first critical thinking (or humility) lesson we have to absorb. We acknowledged that even this concession was probably too generous because our brains are, more often than not, quite deluded and can actually be downright deceptive. This dastardly fatty bundle of cells makes thinking possible, but the catch is that it also makes distorted and deluded thinking highly likely. Therefore, our first lesson on critical thinking is one of humility. All too often, we overestimate our own reasoning ability and underestimate our vulnerability to biases and distortions, even if we can easily see these in others’ reasoning. We need to be modest about what we think and what we believe because we’ve no right to anything so comforting as certainty when it comes to the ability of our brains to accurately form beliefs about the world. Even if we master critical thinking, all of our beliefs and perspectives (even scientific and religious ones) remain tentative approximations, and subject to revision. We should never be dogmatic or rigid in our ideas because we’re actually much more likely to get things wrong than right. This means anything like pride or self-assurance in our own opinions or conclusions is a sure red flag that we haven’t learned the first lesson of critical thinking.
The reality is that our brains have evolved over thousands of years not to get things ‘right’ or get at the ‘truth’ (these terms always deserve inverted commas), but rather to model or estimate the world around us in a way that supports our survival. That means many errors in our thinking are deeply entrenched because they happen to produce an outcome that increases the rate of survival. If we have insane delusions that accidentally improve our survival rate, then over time, these will become hardwired into our brains, and future generations will end up passionately holding to them and willing to die for them. If we survive with certain beliefs, then those beliefs become almost unshakeable – even to the extent that we react emotionally and violently to threats to them. In this way, our brains are both our best friend and our worst enemy. They give us the capacity to think and survive in our environment, but accomplish this by holding us hostage to anything (whether it be delusion or reality) that might increase our chances of survival.
Another of the main reasons (or premises) motivating our desire to learn critical thinking, is that we live in an environment where individuals and corporations actively (and quite skilfully) attempt to co-opt our thinking and beliefs to serve their ideological, political, and financial ends.
Borrowing from Alfred, Lord Tennyson’s famous poem, we could say that our modern information landscape is, in many ways, ‘red in tooth and claw.’ It’s a fiercely competitive arena where ideas clash, misinformation spreads, and attention is a prized commodity. The pairing of our faulty and error-prone thinking with the modern information – and agenda – saturated environment has created a perfect storm within which pushers of ideology, product-marketing, interest groups, and all sorts of ‘peddlers of crazy’ can capitalise. Almost every piece of information, every claim, or idea we encounter is motivated to persuade us of something: to buy something, to vote for someone, to sign something, to click something etc. The list is endless. Therefore, the second critical thinking lesson (or second premise) we learned in Chapter 1 was that our environment is incredibly complex, ambiguous, and mutating. We’re constantly flooded with a barrage of crafty marketing, rhetorical propaganda, clickbait, and ideology-driven ‘news’.
But there was also some good news! A final important premise – and critical thinking lesson – covered in the last chapter was that we can overcome many of the aforementioned vulnerabilities through learning and training. We can retrain our thinking processes to be less error-prone, less distorted, and prejudiced, and, as a result, to get closer to the truth. I also gave reasons why this isn’t just something we should do to improve our own lives, but is an important step toward fulfilling our obligations to our families, communities, and our democratic societies.
So, we can represent most of the claims from Chapter 1 in the form of an argument with several premises and a conclusion – remembering that an argument is a series of statements or sentences (called propositions), where one serves as the conclusion, and the rest, as the premises or reasons to believe the conclusion. Let’s see how this looks for the argument as we’ve laid it out.
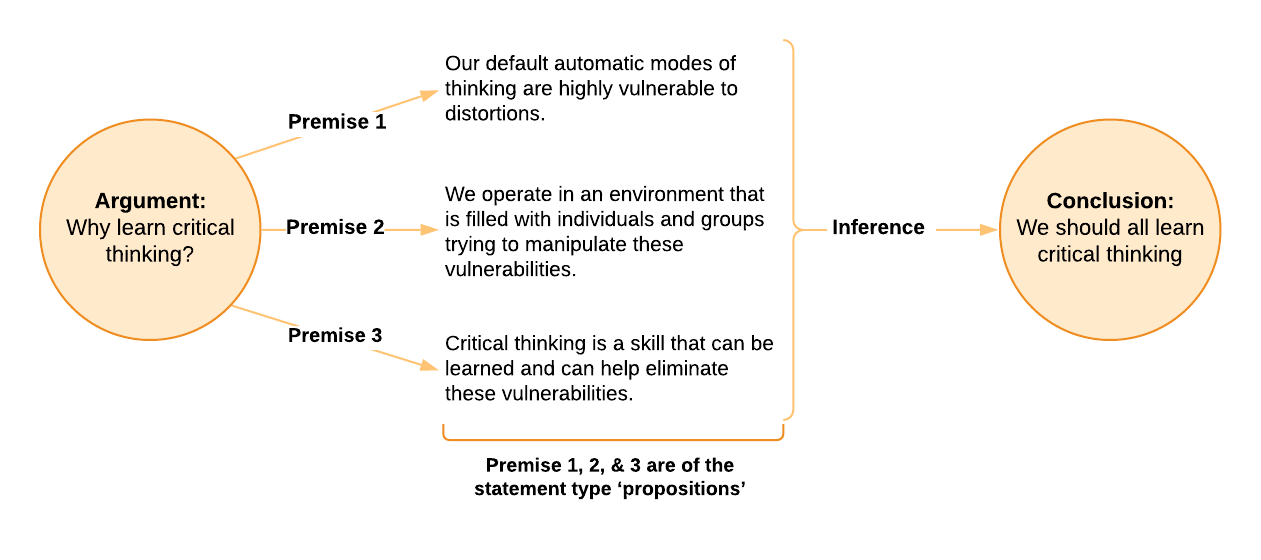
For simplicity, I kept it to three premises (premise three is actually double-barrelled as it is). Our argument has four sentences that are propositions because they claim something about the world that could be either true or false. The first three are the reasons for accepting the final proposition. Therefore, the first three statements must be premises, and the final statement must be a conclusion. Whether you find the conclusions believable will depend on whether you think the propositions that serve as its premises are true or false, and whether you think they support an inference to the conclusion. Stating arguments in this structured way is very helpful in analysing and evaluating them.
That’s enough rehearsal of Chapter 1 – it’s time to get into the meat of Chapter 2.
Steps Necessary to Becoming a Critical Thinker
In his useful book on critical thinking, Joe Lau (2011)[2] outlines the three steps that are necessary for us to become a successful critical thinker:
- Theory: Developing knowledge
- Application: Practising skilful application of critical thinking
- Attitude: Holding the right mindset and disposition
This chapter will deal with each of the parts of these three steps briefly, and they’ll be fleshed out more in future chapters.
1. Theory: Developing knowledge
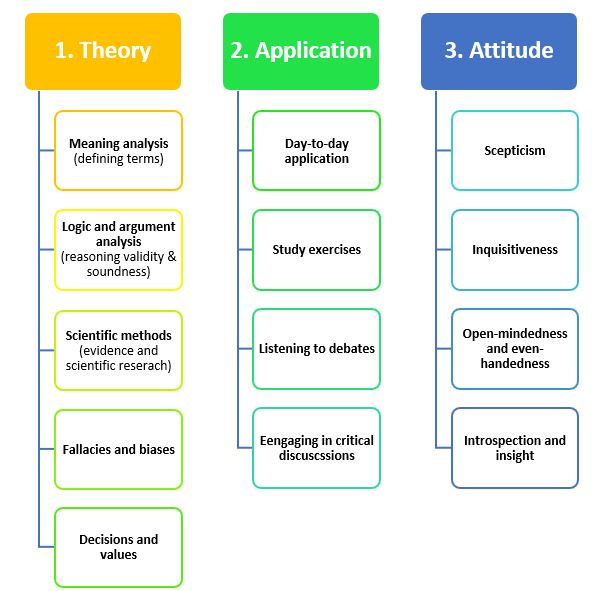
The theoretical knowledge required to be a skilful thinker can be quite complex and even a bit daunting. Thinking is an enormous subject area with many sub-fields and many interesting rabbit holes to get lost down. Thankfully, critical thinking expert Lau (2011) organises the necessary theoretical knowledge for critical thinking into five key areas:
- Meaning analysis
- Logic and argument analysis
- Scientific methods
- Fallacies and biases
- Decision and values.
Each of these areas involves a decisive set of appraisals (appraisal topics 1 through 5, so to speak) that we must make to properly think critically about any issue we face.
‘Appraisal’: Unlike the other technical terms, this one is fairly commonplace, but because it represents such a central activity in critical thinking, I thought it deserved spelling out. An appraisal is an assessment or evaluation. We appraise something to examine its qualities, acceptability, merit, or persuasiveness. Most of us are familiar with examples like performance appraisals at work.
Meaning Analysis
The famous Scottish philosopher, Thomas Reid, put it right when he said, ‘There is no greater impediment to the advancement of knowledge than the ambiguity of words’. And the great Voltaire also understood the importance of clear definitions when he demanded:

Lastly, one more from the greatest philosopher of language of all time, Ludwig Wittgenstein:

Wittgenstein points out that if you’re not saying something clearly, you’re really not saying anything at all. Language is so central to knowledge, truth, and logic that a whole chapter (Chapter 5) of this book is devoted to it.
Meaning analysis is the foundation stone of any examination or discussion of ideas. Our first step in scrutinising any claim is the ‘appraisal of meaning’. We need to be clear on what the terms or concepts of any proposition actually mean. This can be much more difficult than you might think. Concepts and terms carry multiple – often conflicting – meanings, depending on the context and person involved. Clear thinking and clear reasoning begin with conceptual clarity. Almost everyone has had the experience of debating with someone, where the discussion simply gets bogged down in differences over definitions and everyone ends up talking about different things. The study of meaning is a field of its own and is called ‘semantics’.
‘Semantics’: The study of meaning in language, such as the interpretations of words.
One of the most important steps in assessing or discussing ideas is to settle on definitions for the key terms or concepts. Clarity of thought requires clarity of meaning. We can’t begin to think about ideas until we know what we mean by the words used to represent them. Thinking is largely a linguistic thing, which means it’s something done predominantly with words. Yet, words can be slippery shapeshifting critters that seem to resist being nailed down. Regardless, it’s very hazardous and reckless to form beliefs or take positions on issues before you’re completely clear what each of the key terms mean. Seek out conceptual clarity as a first step in forming reasonable ideas. Arguments are built up from propositions (that serve as premises and conclusions), and propositions are built up from terms (words) that must have clear definitions. The truth of a proposition can’t be assessed until we know what it’s actually about.
If you’ve seen (or been in) debates with intellectual or careful thinking people, you might hear the expression ‘Well, that depends on what you mean by…’. This can sometimes seem like a tricky evasion technique, but more likely, it’s because there’s no way to form or defend a position on something before you know what is meant by the key terms. Careful thinkers will demand clear definitions of the terms before committing to a position. Others just use this tactic to hide their ignorance or get out of committing to a position.
In this way, conceptual clarity is also a necessary precondition to sharing ideas with others. I was having a debate with someone just the other day about whether systematic racism exists in modern Western societies like Australia and the United States of America. There really isn’t any way to provide reasons and evidence for or against any proposition before everyone can agree on what key terms like ‘racism’ and ‘systematic’ mean. If we can’t agree on the meaning of these terms, meaningful discussion becomes impossible. In many cases like this, you might find that disagreements are actually superficial and merely boil down to sloppy or inconsistent definitions. However, few things in a dialogue can be more frustrating than someone shifting definitions mid-conversation. Debates like this go nowhere as individuals talk past each other or try to keep up with a shifting target as the topic changes. If you’re in a discussion with someone, you must pin down what they mean by the terms being used. You must be clear about how you’re using the terms. You don’t need to agree on definitions, but you do need to know what you’re each talking about. Sometimes just identifying an incompatible definition can clarify plenty of disagreements.
Some rules of engagement to guide in having a clear and productive exchange of ideas:
- Everyone must be clear and open about the meaning of the terms.
- Everyone should try as much as possible to use the terms to mean the same thing.
- Everyone must be committed to not changing definitions (no shifting of goalposts).
Words have many layers of meaning, and there is no such thing as a ‘correct’ or ‘incorrect’ definition, no matter how ridiculous we might think someone else’s definition is. We simply choose – usually based on conventions that are enshrined in dictionaries – whether we accept certain definitions or not. Even the dictionary definition of words is ‘descriptive’, not ‘prescriptive’. This means the dictionary attempts to capture the common ways words are used in society, not to dictate to society how to use a word. Otherwise, the dictionary wouldn’t be changing its definitions and adding new words yearly. You can reject someone’s argument on the basis that their definition is unsatisfactory, but that doesn’t mean their definition is wrong.
Outside a specific discussion, we don’t all need to use words to mean the same thing, as long as we’re clear and consistent with our definition. Someone might claim that they’re very strong. Of course, the first thing to do with a claim like this is to have them define what exactly they mean by strong. They might say they believe strength is the ability to lift 50 per cent of their body weight. You don’t need to dispute their definition if you think ‘strong’ actually means being able to lift 100 per cent of one’s body weight. You simply understand their claim better now, and on the basis of this, you can decide whether you’re convinced by their claim to be strong or not.
One thing to be careful about, though, is disingenuous redefining of words in order to capitalise on the rhetorical power of certain phrases. For example, the accusation of ‘Nazi’ these days is a very powerful weapon to use on someone with an opposing political or social viewpoint. Accusations like these quickly render a person’s argument illegitimate and silences their voice. If someone is genuinely a racist white supremacist, then perhaps their silence is entirely warranted. But if someone simply holds a classically liberal or central-conservative position on political or economic issues, then it’s clearly an underhanded rhetorical tactic to label and dismiss this person in order to avoid having to address their actual arguments. Many people use the same tactic to dismiss people with left-leaning ideological stances as mere ‘Communists’. Labels like ‘racist’, ‘sexist’, ‘homophobe’ or ‘Nazi’ are ineffective responses to ideological positions that we don’t agree with, but can’t dismiss with reason or evidence. This type of tactic is also a logical fallacy called ‘ad hominem’ (more on this in an upcoming chapter). We’ll discuss fallacies more soon, but one of the most important things to keep in mind is that fallacy doesn’t mean false. It just means vulnerable, and represents an uncertain or unreliable way to reason. The ad hominem is fallacious because a person’s moral position or worth has no bearing at all on their argument. Maybe you tell me that 2+2=4, but then I find out you like to strangle cats on your weekends. This new information about you has no bearing whatsoever on your argument about addition. I can reject your invitation to hang out next weekend, but I don’t have any reason to reject your claim that 2+2=4.
‘Fallacy’: A fallacy is a logical mistake in an argument. It’s an instance of faulty reasoning that makes an argument invalid or unconvincing. To commit a fallacy means to violate the rules of engagement. An argument containing a fallacy might be easily dismissible. If I said, ‘All As are Bs’ and ‘All Bs are Cs’, and then I conclude that ‘No As are Cs’, you know I’ve violated the rules of the game. In this case, you could dismiss my conclusion because it’s fallacious and obviously incorrect. A fallacy doesn’t mean the conclusion of the argument is incorrect – even bad arguments sometimes stumble on true conclusions. The commission of a fallacy just means the argument isn’t convincing, no matter how true the conclusion actually is. A valid deductive argument – meaning one that commits no fallacies – forces you to believe the conclusion. As in, if the premises are true, the truth of the conclusion is inescapable. So, ‘fallacy’ doesn’t mean ‘false’ (everything in the argument could still be true), it means ‘unconvincing’ or a violation of the rules of the reasoning game, and for this reason, a fallacious argument doesn’t give us any worthwhile reason to believe the conclusion.
Words are always rhetorical weapons and must be respected and used with responsibility. Be on the lookout as people on all sides of religious, political, and ideological lines attempt to do sneaky things with language to gain an advantage and score cheap points.
‘Rhetorical’: Rhetorical is concerned with the art of persuasion. Rhetorical acts are speech or writing that’s intended to express and influence others to adopt a certain point of view, or to see the world a specific way. A rhetorical tactic or rhetorical weapon is a use of speech or writing to make a decisive point, to win an argument, to persuade someone, etc. Much of what we’ll deal with in this critical thinking text is how to use and navigate rhetorical tools in our interactions with others.
Logic and argument analysis
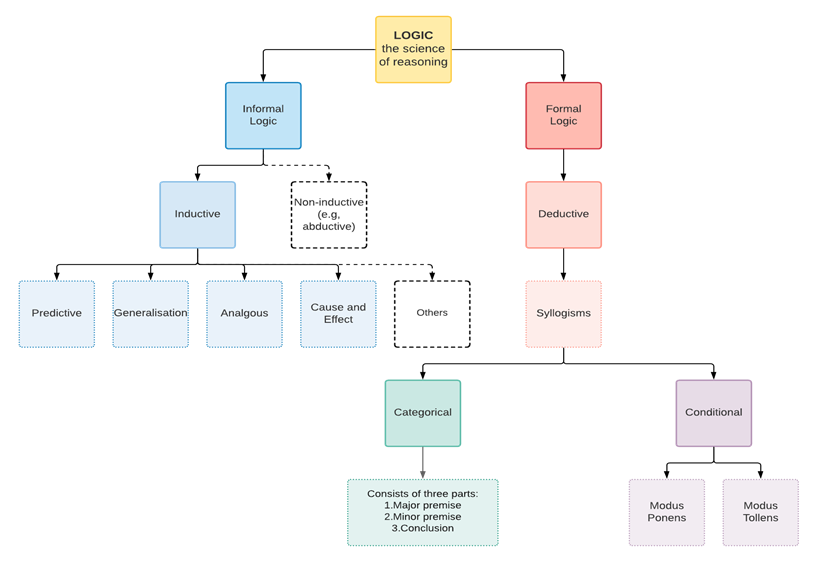
Following the clarification of meanings, the next step in scrutinising any claim is the ‘appraisal of reasons’. The topic of reasons is fascinating because it can be quite subjective – whether a reason for something is compelling to you or not is a personal judgement you make – but is also objective in that there is also a formal science called ‘logic’ that studies legitimate forms of reasoning. Logic is the formation and study of rules or principles that govern how we reason. Studying logic isn’t always very interesting, but as famous historian Will Durant put it, ‘Nothing is as dull as logic and nothing is so important’. The rules of logic are like a formal way of outlining the moves that are legitimate and illegitimate when it comes to the game of thinking. These rules – or principles – give us criteria we can use to pick out which inferences are valid, and which are not. Invalid reasoning violates the rules of the game and leads to faulty, rubbish conclusions.
Logic is the science of reasoning, and is usually divided into formal and informal types. Formal logic is known as deductive logic, and includes types of arguments that are called syllogisms, among others. Informal logic includes inductive and other non-deductive forms of reasoning (e.g. abductive, which we won’t cover in this book). The first thing students need to master is this important distinction between inductive and deductive types of reasoning. Then in later chapters, we’ll cover specific forms of formal (deductive) logic called categorical syllogisms, modus ponens, and modus tollens. We’ll also learn specific forms of informal (inductive) reasoning covering four main types: generalisation, analogous, predictive, and causal inductions. All of these types of logic are powerful tools you can use to work out what exactly is reasonable to believe. Identifying what is a reasonable conclusion is a matter of knowing what inferences are justified by a certain argument.
To make an ‘inference’ is to draw a conclusion on the basis of reason or evidence. An inference is like ‘jumping to conclusions’ but with some reason and evidence. We’ve already performed some inferences in the arguments we showed above. An inference is nothing other than the step from certain propositions that serve as premises, to new propositions, which are conclusions. This jump from known (or just assumed) premises to a new fact is called an inference. In the above example arguments, we performed an inference when we arrived at the conclusions. In your other psychology study, you’ll learn about drawing statistical inferences on the basis of sampled data to a conclusion about the sampled population (inferential statistics are all about going from what’s known about a sample to learning something new about a population). In the simplest terms, drawing a conclusion on the basis of premises is making an inference. However, now all inferences are justifiable since they must be based on certain rules in order to be valid.
To understand the power of inference, look at the following logic puzzle:
Salim, Jack, Bob, Neil, David, Mike and Krish own different types of cars (Honda, Jaguar, Audi, Suzuki, BMW, Ford, or Toyota) and play different sports (tennis, badminton, and or cricket). From the following propositions (which don’t tell us all the information), we can infer the type of car, and the type of sport, each person owns/plays. This is the power of inference: it allows us to use limited information we have access to in order to work out more information.
- Mike owns a Ford and doesn’t play tennis.
- Neil owns an Audi and plays tennis.
- Salim doesn’t play tennis.
- Jack doesn’t own a Toyota.
- Krish is the only badminton player apart from Jack.
- David owns a Suzuki and doesn’t play tennis.
- Neither the Jaguar owner nor the BMW owner, plays cricket.
- The Toyota owner plays badminton.
- Bob doesn’t own a BMW.
See if you can work out who plays which sport and who owns what type of car. The answers will be at the end of the chapter.
‘Validity’: When referring to logic and inferences, a valid move is a legal one or a justifiable one – meaning it follows the rules of the game and is reasonable. Therefore, validity is all about what is reasonable to conclude when making inferences. A valid argument means accepting that the premises are true, which forces us to accept that the conclusion is true. To determine if an argument is valid, ask yourself, ‘If the premises are true, are we locked into the conclusion?’.
An area that confuses many students is trying to interrogate the truth of the premises to demine validity. The truth of the premises has nothing to do with the validity of the inference and whether the argument is deductive and inductive. The truth of the premises is, therefore, something totally different from deciding if the argument is deductive or inductive. The premises don’t need to be true, or even meaningful (a premise could be ‘All grinks are dinks’, which means nothing, but may be an acceptable premise in a valid deductive argument). To determine if an inference is valid, we just assume the premises are true, and then figure out if accepting them as true makes the conclusion necessary and inescapably true. If so, we have a valid inference and a valid deductive argument. The next step is, of course, to try determining whether the premises are, in fact, true, to then determine if we have a ‘sound’ argument, and if so, we can actually accept the conclusion as true.
If you’re studying psychology, you’ll hear the word validity referring to many different things. In experimental design, you’ll learn about the internal and external validity of experimental procedures. In psychological measurement, you’ll learn about the psychometric validity of instruments. In this book, we’ll focus on the validity of arguments and their inferences. In all these cases, validity means something like ‘true’ and ‘correct.’ In logic, an argument is invalid if the inference isn’t appropriate or can’t be supported by the premises.
Once you’ve read the definition of ‘validity’ in the Technical Term Box above, let’s look at an example:
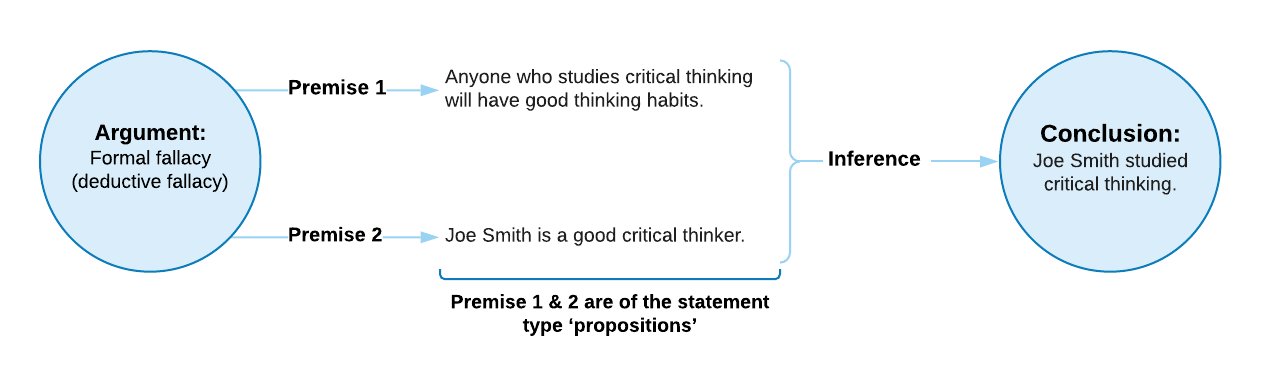
You can see that this conclusion does not necessarily follow from the premises. The key word here is ‘necessarily’, which means there could be a million different reasons Joe is good at thinking, and yet still not have studied critical thinking – though this seems unlikely, it’s possible. We’ll go into detail on the actual rules of inference that this example violates in Chapter 6.
A sillier example will make the faulty reasoning here obvious:
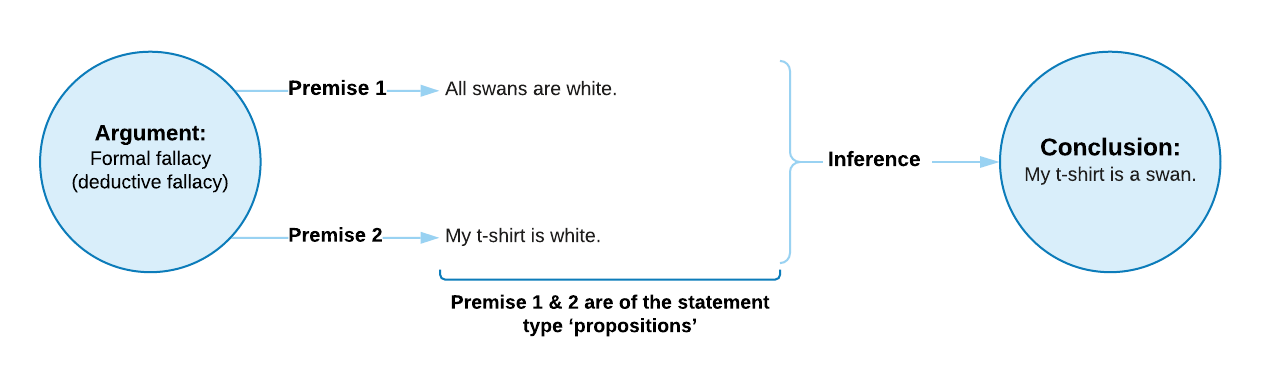
Generally, arguments fail for two primary reasons:
- (1) the premises are simply untrue (so the argument would be false), and/or
- (2) the inferential move from the premises to the conclusion is invalid because the premises, if true, don’t make the conclusion certain.
When the inferential move isn’t guaranteed, it’s called a deductively invalid argument because you can’t definitely deduce or infer the conclusion from the premises. Because the conclusion from the above example can’t be derived ‘necessarily’ from the premises, it commits a formal logical fallacy called the non sequitur (which is Latin, and literally means ‘it does not follow’ or ‘not in sequence’ – we’ll go into this more in Chapter 6). The technical term for arguments with true premises and with valid inferences is ‘sound’.
We can see the example arguments above are invalid, but we might also reject them on the grounds of falseness if any of the premises are untrue – maybe Joe Smith is rubbish at thinking, and all swans are definitely not white.
‘Sound’: This is an everyday term that has a special meaning when it comes to logic and analysis of arguments. An argument is considered sound if two conditions are satisfied:
1. the inferential move from the premises to the conclusion is valid, and
2. the premises are actually true.
This means the propositions that serve as the premises actually need to be true for the argument to qualify as a ‘sound’ argument.
In this way, an argument that’s invalid is also unsound. But an argument can also be valid and still unsound if the premises are false. That is to say, premises that could be untrue might still produce a valid inference.
An area that some students get confused is in not appreciating the difference between analysing the validity of the inference and analysing the truth of the premises. These are different things and are usually unrelated to each other. A valid inference doesn’t tell us anything about the truth of the premises, and true premises don’t tell us anything about the validity of the inference.
Whether an inference is valid or not has to do with whether accepting the premises (we accept them just for the sake of argument) force us to accept the conclusion. This isn’t to say we always accept the premises – we just do so in order to analyse whether the inference is valid. It’s also important to analyse the truthfulness of the premises, but this has nothing to do with analysing the validity of the inference. A valid inference (assumed premises force us to accept the conclusion) is the distinguishing feature of deductive and inductive arguments, however the truthfulness of the premises doesn’t help us distinguish between inductive and deductive arguments in any way. Sound and valid arguments contain true premises and valid inferences, which means they’re clearly justified by the premises. In a later chapter, we’ll go into much more detail about how and when inferences are valid and how to detect invalid inferences. What we’ve been talking about here pertains to types of arguments that are ‘deductive’.
Logical arguments are often divided into two types: deductive and inductive. A deductive argument is one that guarantees the conclusion from the premises. By definition, the conclusion of a deductively sound argument is inescapable. Deductive arguments are those arguments in which, if we accept the truth of the premises, we have to accept the truth of the conclusion – it’s necessarily true if the premises are true. For example, this is how I know that Krish plays Badminton and drives a Toyota from the logic puzzle above. For a deductively valid argument, the conclusion has to be true if the premises are true, which means the inference is rock solid. In contrast, an inductive argument doesn’t guarantee anything – an inductive argument can have true premises and still have a false conclusion. This will never happen with a valid deductive argument. This is how you distinguish between a deductive and an inductive argument. Ask yourself, ‘Is there any way the conclusion could still be false if the premises are actually true?’. If the answer is ‘No’, you’re dealing with deduction. If the answer is ‘Yes’, you may be dealing with induction.
This distinction can be confusing to some people, so I’ll risk repetitiveness in order to emphasise it again. A deductive argument is one in which, if we were to accept the truth of the premises, we are forced to then accept the truth of the conclusion because the premises render the conclusion inescapable. That is, a deductive argument is one in which the conclusion can’t be false if the premises are true. In contrast, induction is a catch-all category that contains any argument that fails this criterion of deduction (i.e. true premises making the truth of the conclusion absolutely certain). An inductive argument is one in which assuming the truth of the premises makes the conclusion more ‘believable’, but not certain. That is, an inductive argument is one in which the conclusion can be false even though the premises are true, but a good inductive argument has premises that make the conclusion more believable, even though it isn’t absolutely necessarily true, as in deduction. Also, keep in mind that the truth of the premises is a different analysis altogether and isn’t a distinguishing factor. An argument that has a valid inference and true premises is called ‘sound’. This is the only real difference between induction and deduction. If you try googling differences between the two, you’ll come across plenty of other descriptions that are incorrect – so while I normally recommend googling the concepts in this text to learn more about them, this is one where you’ll be led astray.
Therefore, what we’ve learned so far about valid inferences, represents the strictest case of deductive arguments. And these conditions are usually considered too strict for everyday use. Most of our everyday reasoning – and most of scientific reasoning – is actually inductive, which is to say smuggles in some invalidity (commits formal fallacies), in the interest of building knowledge. Inductive arguments are forms of reasoning that violate the strict deductive – or formal – rules of inference, and therefore, commit a formal fallacy in that the structure of the argument isn’t strictly deductively valid. I know that’s a mouthful, but don’t worry, I’ll unpack it.
Let’s go back over it slowly. Inductive arguments are a more common and less strict type of logic. A proper definition might be: ‘Inductive reasoning is any reasoning that’s formally invalid’ – that is, on the widest conception of it, whatever isn’t deductively valid can fall into the category of induction. When I say invalid, I don’t mean worthless or wrong – only that it’s uncertain, or has a reasonable chance of being wrong. Therefore, inductive arguments are deductively invalid, which is to say, they commit a formal logical fallacy called the non sequitur (more on this later), but they’re still considered worthwhile in many situations. Thus, to be formally invalid just means that the argument or reasoning is insecure and error-prone.
The reason inductive arguments are deductively invalid is because they can contain true premises and a false conclusion. That is to say, these arguments contain premises that don’t guarantee the conclusion, but rather, are believed to make the conclusion more likely. Inductive arguments can still be strong arguments if they have premises that give good reasons for believing their conclusion, but are merely convincing, not certain. We typically judge deductive arguments on their soundness, which is made up of their validity and truthfulness of premises. In comparison, we judge inductive arguments on their strength, though always acknowledging that due to the affliction of the non sequitur, they can turn out to be wrong, no matter how strong they are. This is the uncertainty we accept as payment for tolerating the formal fallacy.
Let’s have another look at our friend Joe:
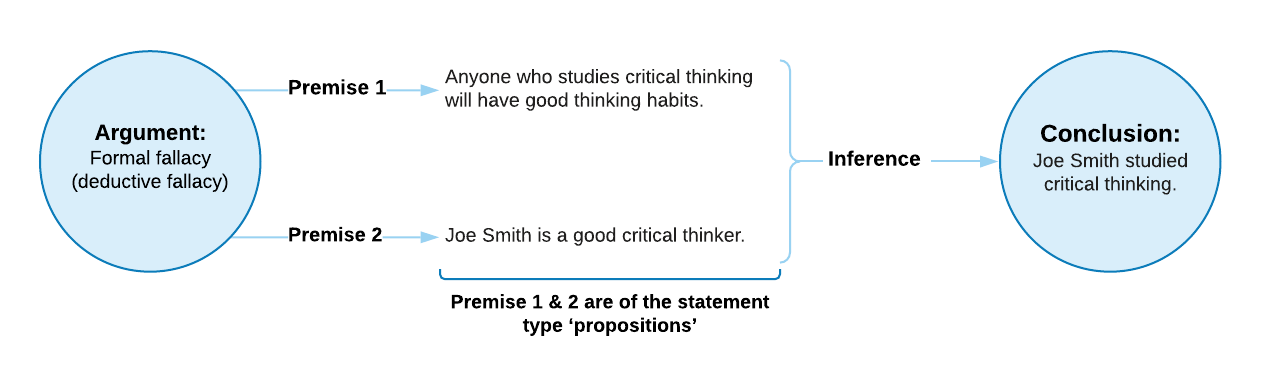
We’ve already concluded this argument is deductively invalid because it commits the non sequitur, and we learned that this meant that the truth of the conclusion isn’t guaranteed by the truth of the premises (i.e. ‘it does not follow’). However, it could be offered as an inductive argument, which means the premises are not thought to guarantee the conclusion, but just make it more believable. In this case, we would have to decide how strong the argument is, which is to say how convincing it is – how believable is the conclusion, in light of the premises offered to support it. This is more of a subjective judgement, and we would have to admit the premises aren’t really good reasons for the conclusion. Inductive arguments are more flexible than deductive arguments, in that you can strengthen them by adding more reasons or evidence to serve as new premises. Premises in inductive arguments must also be scrutinised by looking for informal fallacies, which we’ll discuss in great detail soon. Let’s settle for a simple example here.
A forceful (which is to say convincing) inductive argument could be:

No matter how strong it is, this conclusion might be a case of ‘famous last words’ as an exploding sun wipes us all out and makes reading this chapter the saddest possible way to spend your final moments.
As you can tell from this brief introduction to logic, the principle focus of logic is arguments and inferences within arguments. An argument is the most common form of reasoning, so throughout the text, we’ll learn a lot about their structure and what can go wrong with them. Even if most of the reasoning you’re exposed to isn’t stated in the form of a structured argument, there is invariably a set of premises underlying almost every claim. Identifying what the claim or conclusion is, and then evaluating the premises (hidden or not),[3] is the major task in appraising reasons and reasoning.
Answers to the logic puzzle:
| MAN | CAR | SPORT |
| Salim | Honda | Cricket |
| Jack | BWM | Badminton |
| Bob | Jaguar | Tennis |
| Neil | Audi | Tennis |
| David | Suzuki | Cricket |
| Mike | Ford | Cricket |
| Krish | Toyota | Badminton |
- Arguments require only two statements: one premise and one conclusion. Categorical syllogisms – which are a special type of deductive argument – require three: at least two premises and one conclusion. Some students confuse these principles, so beware of the difference. ↵
- https://www.google.com.au/books/edition/An_Introduction_to_Critical_Thinking_and/KCOeRQW2s0cC?hl=en&gbpv=0 ↵
- Hidden premises are sometimes called ‘implicit premises’ because they’re not stated explicitly or openly in the argument. The use of implicit premises may be inadvertent, but might also be an intentional and sneaky way of hiding premises that are self-evidently untrue or useless in supporting the conclusion. When appraising arguments, be on the lookout for implicit premises that are not openly offered, but the arguer might intend that you believe or accept it in order for the conclusion to be believable or acceptable. Premises should never be implicit. For any claim to be taken seriously, all premises must be open and available for scrutiny. Demand all the reasons and evidence behind any claim. ↵

