Chapter 6, Part B. Constructing and Appraising Arguments
Learning Objectives
- Understand the distinction between categorical deductive and conditional deductive arguments
- Be able to identify and distinguish between modus ponens and modus tollens
- Be able to detect fallacious conditional arguments
- Understand the use of deduction in deriving scientific hypotheses (observational consequences of theoretical propositions)
- Understand the uses of deduction in falsifying scientific evidence
- Understand the uses of induction in confirming scientific evidence
- Distinguish between the four types of induction
- Identify the types of premises and assumptions on which the four types of induction depend.
New Concepts to Master
- Conditional or hypothetical argument
- Modus Ponens
- Modus Tollens
- Affirming the antecedent
- Denying the consequent
- Affirming the consequent
- Denying the antecedent
- Generalising induction
- Analogous induction
- Predictive induction
- Causal induction.
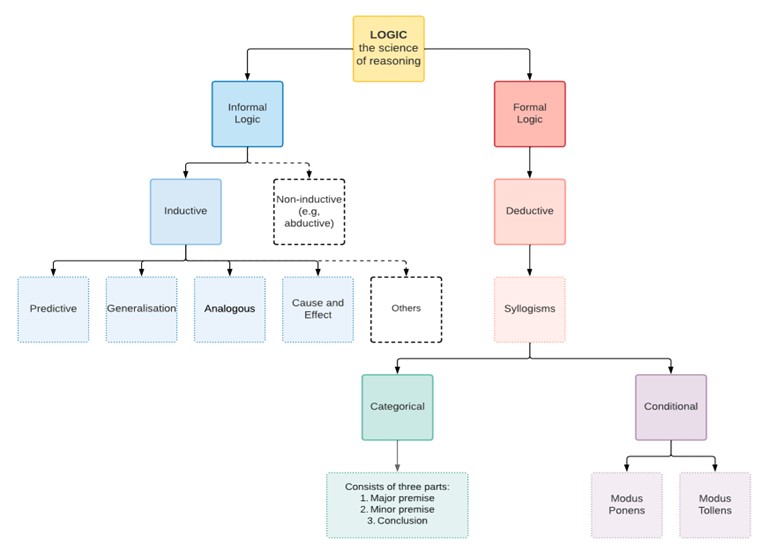
Conditional or hypothetical Arguments: Modus Ponens and Modus Tollens
The propositions in the preceding syllogisms were categorical because they made claims about all, some, or no members of one class or group belonging to another class or group. The next group of deductive arguments we’ll learn are called conditional or hypothetical arguments because these express a condition or relation of dependence between propositions and terms. This is another form of deduction that we’ve seen before in this text, but in this chapter, it will get the fuller treatment it deserves. Modus ponens (Latin for ‘way of affirming’) and modus tollens (Latin for ‘way of denying’) represent arguments in which inferences can be drawn from a conditional proposition. A conditional proposition has the form ‘If A, then B’. Symbolically, we write this as A ⊃ B, where the sideways horseshoe symbol (⊃) represents the ‘If . . . then’ connection between terms (sometimes in notation an arrow → is used instead of the sideways horseshoe). The symbol ‘¬’ means ‘not’ and so if it’s before a term, the proposition is that this term isn’t observed or doesn’t obtain (another way of saying that something is being defined). The other symbol to take note of is the triangle of three dots ‘∴’, which just means ‘therefore’, and tells you that you’ve reached the conclusion.
‘Conditional or hypothetical syllogism’, ‘Modus Ponens‘ and ‘Modus Tollens’: A hypothetical syllogism or hypothetical argument is a two-premise argument like the categorical syllogism, but one of the premises is a hypothetical or conditional (‘if … then’) type of proposition. This hypothetical proposition contains two parts: the ‘if’ part is called the antecedent, and the ‘then’ part is called the consequent. Typically, hypothetical arguments contain a second premise that’s a categorical premise, and a categorical conclusion, just like the syllogisms we’ve learned about above. In this way, hypothetical or conditional syllogisms are similar to categorical syllogisms in having two premises and one conclusion, except the major premise is a hypothetical or conditional type of statement.
Two major modes of hypothetical or conditional syllogisms include the way of affirming, modus ponens, and the way of denying, modus tollens. The key factor in distinguishing these syllogisms is the affirmative or negative quality of the second premise.
Look at the following examples:
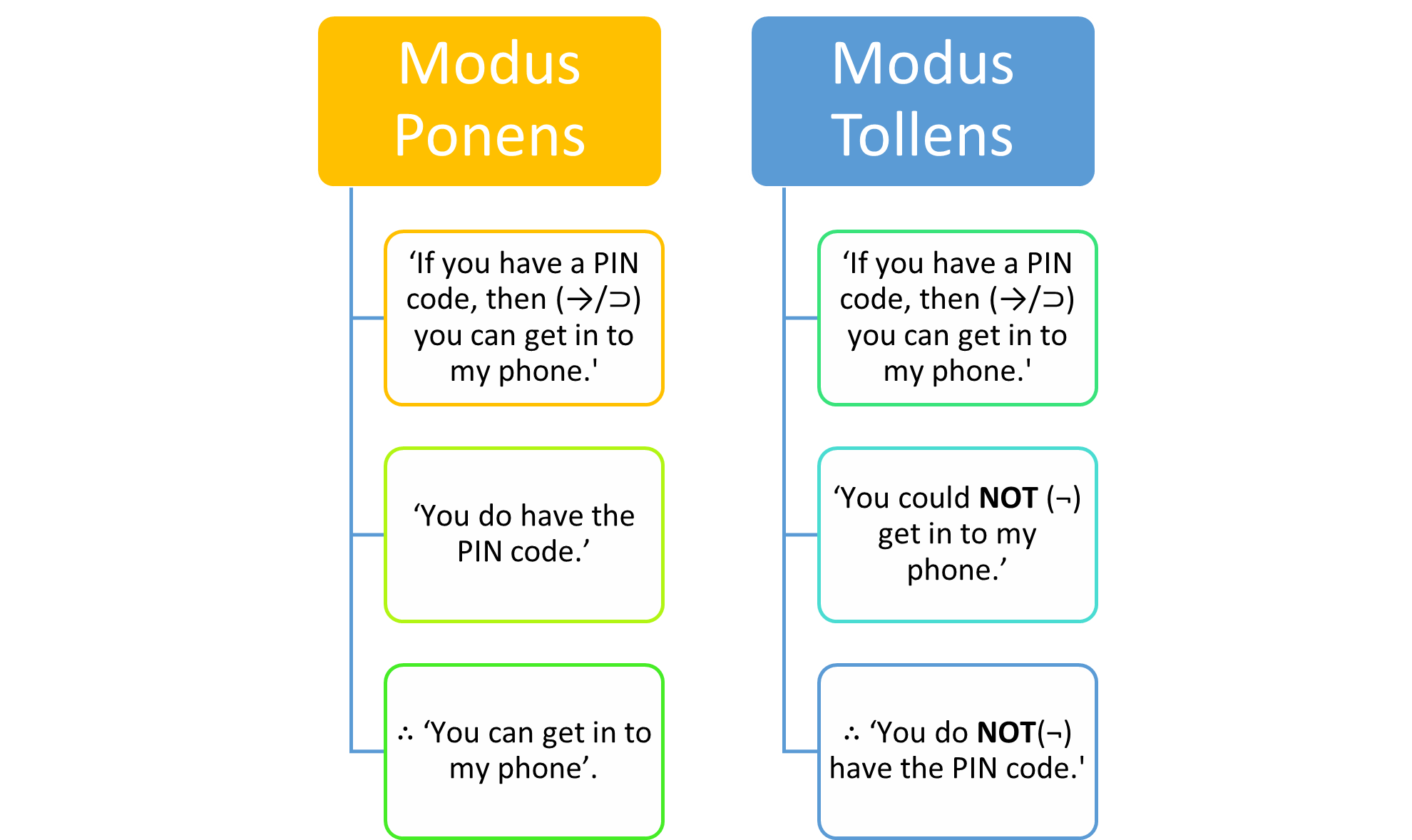
As you can see, the modus ponens is more direct, while the modus tollens is a more indirect form of reasoning. Like all deductive arguments, this argument form is valid if – no matter the content of the statements – when the premises are all true, the conclusion must be true. If we remove the content from the argument, we can look at it more closely:
Modus Ponens:
p→q
p
∴q
Modus Tollens:
p→q
¬q
∴¬p
Don’t worry too much about the notation or symbols here – you’re not required to learn them to follow the main points of conditional reasoning. It’s just easier for me to summarise and illustrate the main points using these notations. For both of the arguments above, the first two statements (i.e. lines) are premises, and the third is the conclusion, which is a pattern you should be very familiar with in deductive arguments. Though these might seem like straightforward conditional arguments, you’d be surprised how often people succumb to fallacies when using or being persuaded by them.
Correct (Valid) and Incorrect (Invalid) Uses of Conditional Arguments
For the rest of this section, I’ll abbreviate Modus Ponens to ‘MP’ and Modus Tollens to ‘MT’. For both forms of conditional arguments, there are corresponding, and very commonly committed fallacies. To understand the fallacies, we need to understand two more names for the pieces of these conditional arguments. For the conditional proposition ‘p→q’, p is called the antecedent, and q is called the consequent. This is straightforward enough since in this argument, q is considered a consequence of p, which antecedes or comes before it. Knowing this distinction is important because it’s by using these names that the corresponding fallacies are identified.
MP is therefore said to affirm the antecedent because the p is affirmed in the second premise. Conversely, MT is said to deny the consequent because the q is denied in the second premise. These are both valid premises and lead to valid conclusions.
Modus ponens (affirming the antecedent) and modus tollens (denying the consequent) are two valid forms of conditional arguments. These Latin names describe the way the arguments proceed, rather than the specific content of their premises.
When valid, modus ponens affirms the antecedent in the second categorical premise, and therefore, can support an affirming categorical conclusion.
When valid, modus tollens denies the consequent in the second categorical premise, and therefore, can support a negating categorical conclusion.
There are two corresponding fallacious forms of reasoning that occur quite often. The first is called affirming the consequent, which happens when we argue from p→q, q, ∴p. This fallacy is so named because q is the consequent in the first premise, and yet is affirmed in the second premise, which isn’t a premise that can lead to any certain conclusion. The fallacy of affirming the consequent is also called the converse error.
The other common fallacy is called denying the antecedent, which happens when we argue from p→q, ¬p, ∴¬q. This fallacy is so named because p is the antecedent in the first premise, and yet is denied in the second premise, which isn’t a premise that can lead to any certain conclusion. The fallacy of denying the antecedent is also called the inverse error.
‘Affirming the consequent’ (aka converse error or fallacy of the consequent) and ‘Denying the antecedent’(aka inverse error or inverse fallacy): These are two invalid forms of the standard conditional arguments known as modus ponens and modus tollens, respectively. They are named like this because of a fallacious inference following from the second categorical premise being either affirming or denying.
When invalid, modus ponens affirms the consequent in the second categorical premise, and because of this, can’t support an affirmation of the antecedent as the categorical conclusion.
When invalid, modus tollens denies the antecedent in the second categorical premise, and because of this, can’t support a denial of the consequent as the categorical conclusion.
Remember that because these are deductive arguments, they’re fallacious (or invalid) because the premises can both be true while the conclusion remains false. This is the defining feature of an invalid or fallacious deductive argument.
These are formal fallacies because they concern the structure of the argument, not its content, which is why we can convert all the content to symbols and still see the fallacies. These fallacies render the arguments invalid because the premises can be true, and yet the conclusion false. I’ll illustrate why this is the case with examples soon, but first let’s summarise with the following graphic:
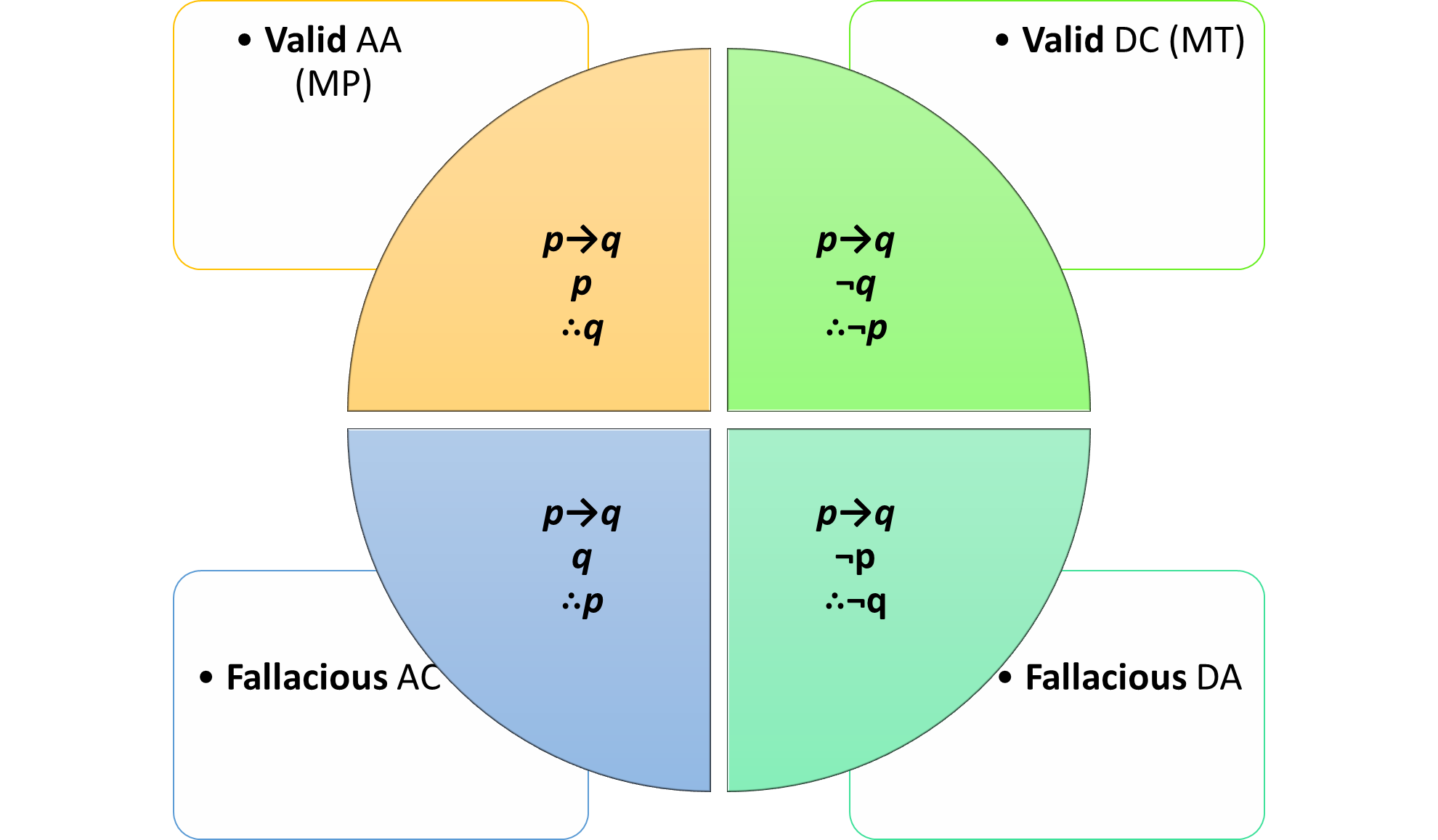
Let’s look at some examples so this can all become a little more concrete.[1]
|
Argument |
Premise 1 |
Premise 2 |
Conclusion |
Status |
|
AA or MP |
If Bill Gates owns Fort Knox† (p), then Bill Gates is rich (q). |
Bill Gates owns Fort Knox (p). |
Bill Gates is rich (∴q). |
Valid though unsound since the second premise is not true (Gates doesn’t own Fort Knox). |
|
DC or MT |
If Bill Gates owns Fort Knox (p), then Bill Gates is rich (q). |
Bill Gates is not rich (q doesn’t hold). |
Bill Gates doesn’t own Fort Knox (∴p doesn’t hold). |
Valid though unsound since the second premise is not true (Gates is, in fact, fabulously rich). |
|
AC |
If Bill Gates owns Fort Knox (p), then Bill Gates is rich (q). |
Bill Gates is rich (q holds). |
Bill Gates owns Fort Knox (∴p). |
Invalid and therefore unsound regardless of the truth of the premises. There are other reasons Bill Gates is rich. The premises in this argument are, in fact, true, but the conclusion is still false, which is the very definition of a fallacious deductive argument. |
|
DA |
If Bill Gates owns Fort Knox (p), then Bill Gates is rich (q). |
Bill Gates doesn’t own Fort Knox (p doesn’t hold). |
Bill Gates is not rich (∴q doesn’t hold). |
Invalid and therefore unsound regardless of the truth of the premises. The premises in this argument are, in fact, true, but the conclusion is still false, which is the very definition of a fallacious deductive argument. |
|
Argument |
Premise 1 |
Premise 2 |
Conclusion |
Status |
|
AA or MP |
If Brian falls from the Eiffel Tower (p), then he is dead (q). |
Brian falls from the Eiffel Tower (p). |
Brian is dead (∴q). |
Valid, though not sure if it is sound because I don’t know Brian, so I don’t know whether he fell or not. |
|
DC or MT |
If Brian falls from the Eiffel Tower (p), then he is dead (q). |
Brian is not dead (q doesn’t hold). |
Brian didn’t fall from the Eiffel Tower (∴p doesn’t hold). |
Valid, though not sure about soundness since I haven’t checked in on Brian lately. |
|
AC |
If Brian falls from the Eiffel Tower (p), then he is dead (q). |
Brian is dead (q holds). |
Brian fell from the Eiffel Tower (∴p). |
Invalid and therefore unsound regardless of the truth of the premises. There are other reasons why Brian might be dead if we discover that he actually is |
|
DA |
If Brian falls from the Eiffel Tower (p), then he is dead (q). |
Brian doesn’t fall from the Eiffel Tower (p doesn’t hold). |
Brian is not dead (∴q doesn’t hold). |
Invalid and therefore unsound regardless of the truth of the premises. |
Table 6.3. Arguments in Valid and Invalid Forms.
† Fort Knox is a United States Army installation which is used to house a large portion of the United States’ official gold reserves.
Revisiting the Wason Selection Task
Remember back in Chapter 3, we confronted the Wason selection task, and at the time, I told you that we would revisit it and learn how to solve it once we had learned some logic. The task is repeated below in case you forgot.
In this puzzle, we’re given four cards with numbers on one face and colours on the opposing face.
- The numbers are either odd or even numbers, and the colours are either blue or green.
- There is a claim about the cards: ‘If a card shows an even number on one face, then its opposite face is blue’.
- The task is to decide which two cards have to be flipped over to test this claim or hypothesis.

he Wason Selection Task is essentially a test of our ability to apply deductive reasoning within a conditional or hypothetical syllogism. The statement “If a card shows an even number on one face, then its opposite face is blue” follows the structure of “If P, then Q,” where P represents the even number and Q represents the blue face.
To determine the truth of this rule, we must identify the cards capable of proving it false (falsification). Recall that only two valid inferences can be made from a conditional proposition: affirming the antecedent (modus ponens) or denying the consequent (modus tollens).
Let’s apply this to the Wason Selection Task. The ‘8’ card represents the antecedent (P), and the green card represents the negation of the consequent (not Q). These are the only two cards that can lead to a valid conclusion and test the rule.
-
Turning over the ‘8’ card and finding a blue face affirms the antecedent (modus ponens) and supports the rule.
-
Turning over the green card and finding an even number denies the consequent (modus tollens) and disproves the rule.
The other cards are irrelevant to testing the rule. The ‘5’ card, representing an odd number (not P), and the blue card, representing the consequent (Q), cannot be used to draw any valid conclusions. Turning them over and reasoning from their hidden faces would be committing a logical fallacy.
In summary, the Wason Selection Task highlights our tendency to focus on confirming evidence (modus ponens) rather than seeking potential falsifications (modus tollens). By understanding the role of both modus ponens and modus tollens in conditional reasoning, we can improve our ability to evaluate the truth of conditional statements and avoid falling into logical traps.
If it is still a little unclear to you, I have a more complete explanation at the end of the chapter.
Conditional and Categorical Syllogisms
It may have occurred to you by now that the major premise of a conditional or hypothetical syllogism is roughly saying the same thing as our old friend categorical proposition type A, but just worded a little differently. That is to say, the proposition ‘All ps are qs’ claims the same thing as ‘If p, then q’. More specifically, if something is a ‘p’, it must be a ‘q’ (conditional) is the same as saying that all the ‘ps are ‘qs (categorical). Let’s look at an example argument stated in each different form to make this connection more concrete:
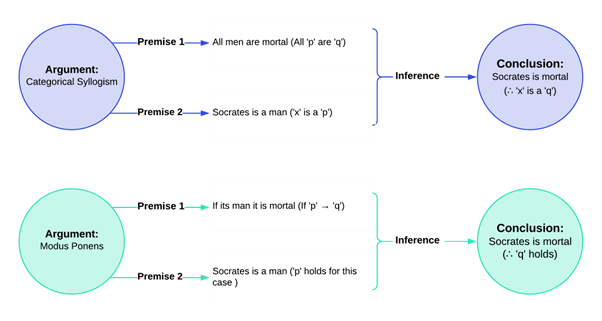
The premises and conclusion basically amount to the same thing.
One final note on deduction because it sometimes gets pigeonholed as an archaic and impossibly ambitious or rigid form of reasoning without any day-to-day implications or applications. This isn’t true at all. Knowing one or two facts about the world can lead us to derive (infer) a range of other conclusions that are implicated by those facts, but we are unaware of. For example, we know that all mammals give birth to live young. So if you’re pet sitting your friend’s pregnant dog, and she goes into labour, though you may never have seen a dog’s birth, or know anything about this process, you can deduce using the major premise that ‘All mammals give birth to live young’, and minor premise, ‘This pregnant pet is a dog’, to the conclusion, ‘It will be giving birth to live young’, which is a certain and necessary deductive conclusion.
Fallacious Scientific Confirmation
I’ve explained several times in this text how an important part of scientific reasoning – how evidence is used to support and confirm theories – relies on formally fallacious reasoning. When done validly, scientific reasoning uses sound deductive reasoning in two ways.
The first way is the use of modus ponens to work out the observational consequences of theoretical claims. Specifically, if p ⊃ q, with p being the theoretical claim, and q being what we would observe if the claim is correct. For the purpose of deriving observation hypotheses, we assume the theoretical claim is correct (p) and ∴ hypothesise that we will observe q. In this way, scientific reasoning uses modus ponens to deductively determine observational hypotheses. And this is a valid use of deductive reasoning.
The second use of sound deductive reasoning is the use of modus tollens when a research study fails to support an observational hypothesis. Specifically, if p ⊃ q, and we observe ¬q because the observational hypothesis wasn’t supported by our study, and therefore, we reject p (conclude ∴¬p). In this way, scientific reasoning and rigorous studies can use modus tollens to deductively falsify theoretical claims. And this is also a valid use of deductive reasoning. We talked in previous chapters about how the use of evidence for falsification is superior to confirmation because it’s deductively valid. Confirmation is always weak and dubious because it’s deductively invalid.
Therefore, the problematic part of scientific reasoning is that there is no deductively sound logical procedure for linking supporting observations to confirm theories (the process of confirmation). When we use the results of scientific studies to support claims about the world, we’re on shaky ground by relying on the fallacious reasoning called affirming the consequent (we argue from p→q, q ∴p).
Let me try illustrating with a very famous case from physics:
|
Argument Form |
Scientific Reasoning |
|
STEP 1: Premise 1: If p ⊃ q. |
If the theory is correct, the observation will be consistent with what the theory predicts. |
|
If the theoretical claim is correct (p) … |
Theoretical premise: Einstein’s theory of general relativity explained that mass distorts time and space … |
|
… we will observe (q). |
Therefore, we will see light being bent as it passes by a very massive object (like the sun). |
|
STEP 2: Organise to carry out the critical observations. |
Astronomers Dyson and Eddington organised an experimental expedition to test the gravitational deflection of starlight passing near the Sun during an eclipse |
|
Now the nature of premise 2 is to be established = does q hold or not. |
If the observation does not reveal starlight deviating because of the sun’s mass, then premise 2 is ¬q |
|
STEP 3: Draw an inference about the theoretical claim. If premise 2 is ¬q, we can rely on Modus Tollens and ¬p is the correct inference. |
If we do not observe the hypothesis (i.e., ¬q), we validly infer the theoretical claim is false. Therefore ¬p When we don’t see starlight bending, we have falsified the theoretical claim, and this inference is deductively rock solid. |
|
When premise two is consistent with the theoretical prediction (as in q holds). |
If the observation does show starlight bending due to the mass of the sun, then premise 2 is ‘q’ (as in q holds) |
|
So now the argument is p→q From this argument, no deductively valid inference is possible. |
Yet from these premises we cannot conclude p or conclude that the theory is proved or true because this is formally invalid and commits the fallacy of affirming the consequent. |
Table 6.4. Scientific reasoning
This is why deduction can’t be used to link confirming evidence with theoretical claims about the world. That form of reasoning is fallacious and is about as reasonable as concluding that because Bill Gates is rich, he must own Fort Knox. So what is to be done? We can’t discard the whole idea of supporting evidence (confirmation). The only way forward is to convert the reasoning into an inductive argument, which, as we know, is always dubious and not deductively valid (hence will always suffer uncertainty). An inductive argument allows us to take instances of supposed supporting evidence as premises, and conclude tentatively that the theoretical claim that gave rise to the hypotheses in the first place is given some small amount of support by each of these. But no matter how many premises (such as that Bill Gates is rich) we accumulate, we’re always just one falsifying (instance of ¬q) away from having to reject the claim that he owns Fort Knox.
The type of induction science relies on in supporting theories is largely intended to uncover universal laws, and so the reasoning is of the form:
- All observed swans are white.
- ∴ All swans are white.
This reasoning is ampliative because the premise refers to observed swans, while the conclusion makes a proposition about all swans, observed or unobserved. The argument is also not truth-preserving, since it’s possible there is a black swan. It isn’t erosion-proof – the observation of one non-white swan would undermine it completely. And its strength is always subjective and a matter of degree, never conclusive.
I’ve put together the following table of uses of logic at each stage of scientific reasoning to help summarise the steps.
|
Reasoning Stage |
Purpose |
Logic used |
Quality of logic |
|
Going from theory to hypotheses |
In order to test a theoretical claim about the world and do research, we need to convert theoretical principles to testable hypotheses, which need to refer to observable events. |
Modus Ponens p→q p ∴q Where p is the theoretical principle and q is the observational consequence of this principle. |
Deductive and valid when done properly. |
|
Conduct the study |
Make observations and collect data. |
– |
Different principles govern collecting data. |
|
IF data falsifies hypotheses |
To refute and eradicate incorrect theoretical principles. |
Modus Tollens p→q Where p is the theoretical principle and q is the observational consequence of this principle. The second premise is then NOT q, and we validly infer from that NOT p so the theoretical principle. |
Deductive and valid when done properly. |
|
IF data confirms hypotheses |
To retain and strengthen confidence in the theoretical principle. |
The temptation (and most scientists do this) is to argue p→q q ∴p But this is to commit the fallacy of ‘affirming the consequent’. What must be done is to formulate a different inductive argument. |
Deductively invalid, but the evidence can be inserted as a premise in an inductive argument. |
Table 6.5. Logic and scientific reasoning.
To rid science of shaky logic (i.e. induction), the famous philosopher of science, Karl Popper, claimed science wasn’t even in the business of the confirmation of theories. He also claimed the discovery or formulation of theories and theoretical propositions was not logical at all, and didn’t need to be. In reality, the discovery and formation of theories is usually inductive as scientists make observations about the world, and then form tentative ideas about possible theoretical propositions, which suggest observational hypotheses to then test. Popper argued quite convincingly that science is, and should be, only concerned with ‘certain’ or decisive reasoning (i.e. deduction), and therefore, focus solely on falsification since that’s all it can do with any certainty. My favourite quote about falsification comes from the French writer Francois de La Rochefoucauld, who wrote: ‘There goes another beautiful theory about to be murdered by a brutal gang of facts’. Benjamin Franklin had his own somewhat plagiarised, but equally poetic version of this when he wrote: ‘One of the great tragedies of life is the murder of a beautiful theory by a gang of brutal facts’.
For some reason, scientists don’t learn elementary logic, and therefore, get egg on their face more times than is necessary (I’m one of them, so I can say that). I care about this problem because it generally corrodes the public trust in science. Even in researching this chapter, I read in one of the most prestigious scientific outlets in the world, regarding the Eddington experiment: ‘the momentous expedition that proved the general theory of relativity’[2], which, as we all know, is an embarrassingly silly statement. This experiment proved nothing, and the word ‘prove’ doesn’t even belong in any scientist’s vernacular. Anyway, this has been a good segue into inductive arguments, which is the topic of the last part of the chapter
|
Hypothesis |
Result of study/test |
Reasoning approach |
Logical form |
Conclusion |
|
If a foetus’s heart rate is higher than 155, you will have a girl |
Girl |
Weak inductive confirmation – based on the theory, my hypothesis said I would observe x (the child will be a girl) and I did observe it (the child was a girl), so my hypothesis and its backing theory is true. |
Affirming the Consequent (or fallacious Modus Ponens):
|
The valid falsification approach is straightforward. When it comes to observing evidence that is consistent with our hypothesis, we run into trouble. Obviously, there are other reasons why the baby was a girl[3], which had nothing to do with the heart rate (since this old-wives’ tale has been falsified) Observing a result that is consistent with a hypothesis does not provide much, if any, support for that hypothesis. All that happened was a failure to falsify it. Confirming observations like this are always, unfortunately, inconclusive. However, observing confirming hypotheses are psychologically so compelling and seductive for us due to our confirmation biases. That is, because of confirmation bias, we mistake corroborating evidence for actual information about the truth of our hypotheses and theories, which they cannot really provide. When it comes to having our pet theories confirmed by evidence, we are the biggest suckers in the world. This is a nasty cognitive bias we need to overcome. |
|
Boy |
Strong deductive falsification – based on the theory, my hypothesis said I would observe x (the child will be a girl) and I did not observe it (the child was a boy), so my hypothesis and its backing theory isn’t true. |
Valid Modus Tollens:
|
Table 6.6. Scientific hypothesis
Inductive Arguments
Arguments that can’t achieve the airtight certainty of deduction aren’t useless. Rather, they’re just inconclusive and fallible, and therefore, should always be held with some scepticism. You’ll see with all four types of induction outlined below that these arguments make audacious leaps into the unknown – about whole populations or classes of cases, about things that merely appear to be similar because they have loads of identical properties, about the future or unobserved cases, or about hidden cause and effect relationships. Since we’re setting out on very shaky ground, we can only hope to be saved by some very careful attention to our procedures for collecting evidence, and with some modesty about the types of conclusions that are warranted.
It isn’t necessarily a problem that we routinely accept arguments that are inductive and uncertain, but we run into trouble when we hold onto inductive arguments as though they were decisive. Inductive arguments are highly prone to yielding false conclusions from true premises. No matter how much it might seem like nonsense, you really have no logical reason for believing the sun will come up tomorrow, but beliefs like this are simply indispensable and are part of how we get through daily life.
The issues with the apparent irrationality of induction were first introduced by Hume, and have become known as ‘the problem of induction’. He pointed out that induction isn’t entirely rational, but at the same time, we simply can’t do without it. See Hume’s quote below on the unjustifiable assumptions inductive reasoning depends on:

Following on from Hume, English philosopher C. D. Broad said ‘induction is the glory of science and the scandal of philosophy’.
We’ll look at several types of induction, though these really all accomplish the same general thing, which is to argue from a series of accepted premises to the likelihood of an unknown conclusion (see the footnote for a link to a more complete discussion and taxonomy of induction types[4]). This is essentially like arguing that the sun has come up every morning of your life, so you infer it will come up tomorrow, which is a type of induction called predictive induction that claims to know things about the future based on observed regularities from the past.
This is a common ‘more of the same’ (the sun will come up again like before) type of inference, and it’s the simplest type of inductive argument. Predictive induction is a weak form of enumerative induction that merely predicts another instance of what has gone before. It has the following form:
Premise(s): All observed instances of A have been X.
Conclusion: The next instance of A will be X.
A strong form of enumerative induction is to generalise from a sample of instances to a whole group or class. We’ll look at this form next.
Generalisation
To generalise from observations is probably the most common type of induction we employ in our day-to-day lives, as well as underpinning most scientific knowledge. The approach here is to argue from observed or sampled instances of a group to the entire group. If you pursue psychology studies, you’ll learn lots about these types of inductions (though they won’t be called by this name), as well as some sophisticated statistical procedures to generalise numerical parameters from sample data.
This type of induction usually takes the form:
Premise(s): All observed instances of A have been X.
Conclusion: All As are X.
‘Generalising induction’: Inferring from a limited number of known instances or cases to a larger population of instances or cases.
In this way, conclusions about all members of a class (or population) are made from observations about a sample of observed members of that class.
An example from Wesley C. Salmon (1984)[5], goes like this:
A time-consuming and expensive quality assurance process is required for a batch of new coffee beans. To save time and money, we decide to test a sample of beans from the batch. Our analysis shows all the sampled beans are in excellent condition. On the basis of this, we conclude that all of the beans in the batch are in excellent condition.
The argument is:
Premise(s): All sampled beans are Grade A.
Conclusion: All beans in the barrel are Grade A.
In this way, we’ve carried out an inductive generalisation. This is actually how quality control works in the real world. The risk, of course, is there’s no way to know if there really is a non-Grade A (e.g. Grade B) bean in the barrel. It isn’t necessary that the generalisation encompass ‘all’ of the class or population, but could be a proportion. For example,
Premise(s): 75 per cent of sampled beans are Grade A.
Conclusion: 75 per cent of beans in the barrel are Grade A.
This type of sampling and induction is very common in everyday life. It’s the foundation of poll and surveys, most psychological studies, and other everyday lessons such as how we learn that fire is hot and shouldn’t be touched (because that experiment yielded painful conclusions previously).
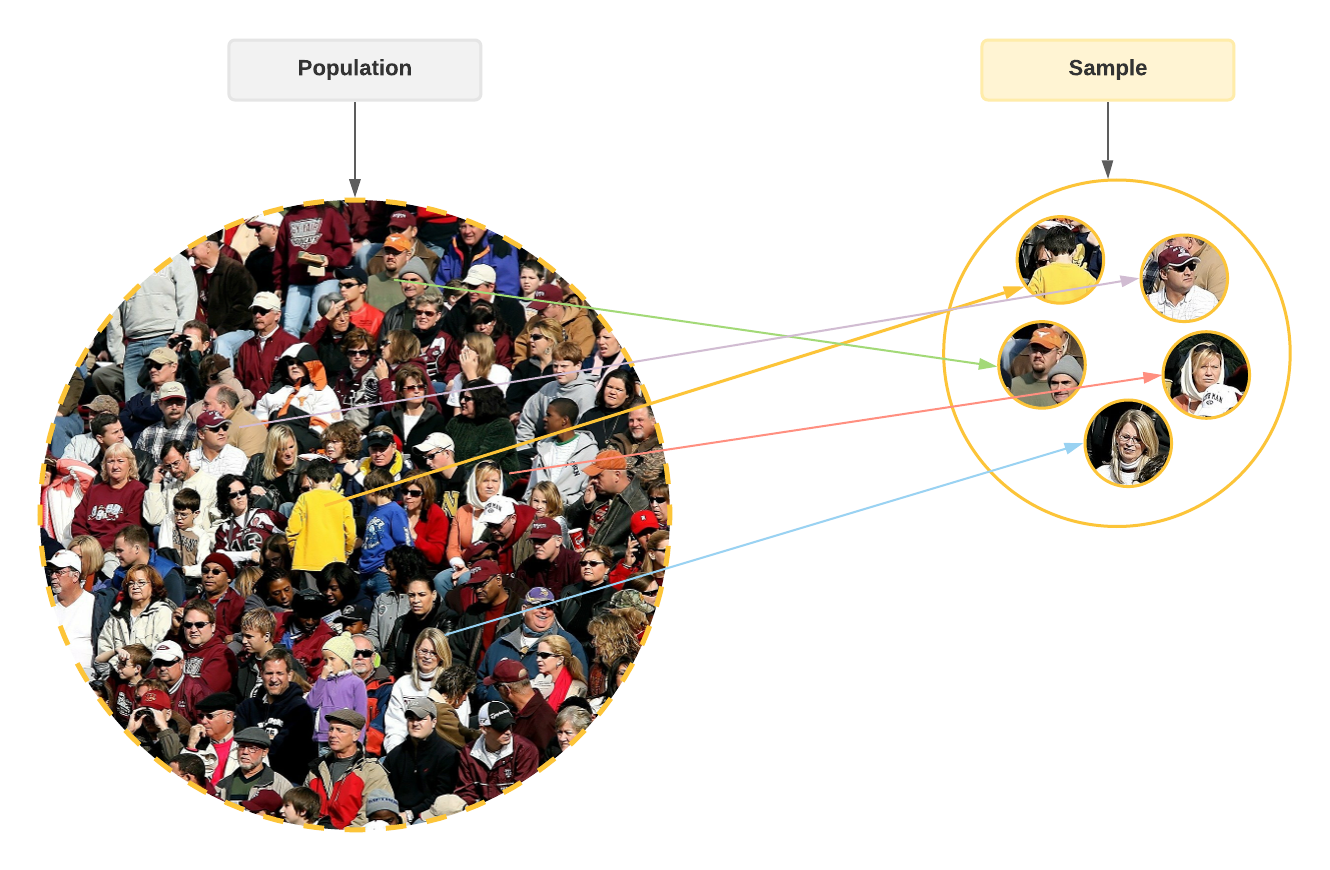
There are a number of pitfalls with these generalisations, and you can probably anticipate some of them already. A major consideration is just how the sample is selected. Biased sampling offers us potentially useless, and worse, misleading conclusions, and yet almost all of our everyday sampling is biased in some way. A true, unbiased sample should be one in which all the elements of the group we want to generalise about are available and have equal chance of being sampled. This is the very definition of a random sample. This is possible with the example of the barrel of coffee beans, but it’s almost never possible with psychological studies or social polls or most things. We never have equal access to every element of the population or group to sample from. No psychological study in history has ever had full access to all living human beings, let alone all human beings from all time. Lots of assumptions have to be met for these arguments to be compelling, such as the nature and extent of the population sampled, the relative size of the sample to the population, and the degree of bias introduced because of the sampling strategy.
Analogous
Analogy – which is another common form of inductive argument – is based on a comparison between objects of different types. Objects of one type are known or assumed to be similar in important ways to the object of the second type. The reasoning proceeds that when certain properties are known of the first thing, and it’s believed the two things are very similar, we can reason, with varying degrees of confidence, that the second thing also has the known properties.
Analogy is a powerful explanatory and rhetorical tool. Analogies give us an emotional (and potentially unjustified) sense of familiarity and certainty about something that’s foreign to us. Using analogies, we get to transfer the sense of familiarity and understanding from one thing that’s understood by us to another thing that isn’t as well understood. However, it can be almost impossible to discriminate which properties are appropriately similar between two things to justify the analogy. In reality, there are almost always as many ways that two things are dissimilar to each other as they are similar. In this way, analogies can lead us astray
Scientists employ analogies in medical research when they use mice or rat models (since rats and humans are physiologically similar) to gain preliminary understandings and develop inferences about disease progression and treatment efficacy and safety in humans.
‘Analogous induction’: Inferring from a known instance or case to another instance or case believed to be similar in relevant respects.
Like all inductive arguments, inferences from analogies can be strong or weak. The form of this argument is[6]:
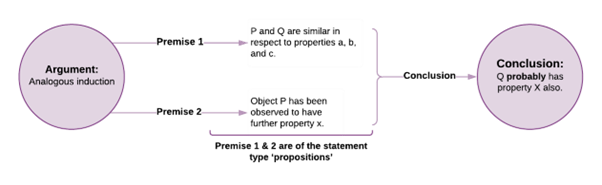
The key term here is the ‘probably’, and it might have sneaked by you, but this term makes all the difference in the world. One of the issues with inductive arguments is that the probability is never calculated explicitly and offered as part of the argument. Sometimes in statistical inferences, probabilities are calculated, but in these cases, it isn’t the probability of the conclusion being right. The calculated p (probability) values only represent the probability of observing what has been found, assuming the conclusion is actually false. In other words, p values from research studies represent the likelihood that, assuming the world is the opposite to how we hypothesise, we would observe the data we have.
Generally, for all inductive arguments, additional unjustifiable assumptions about the uniformity of nature across instances or over time are required. Yet, it simply isn’t possible to justify the needed assumptions that the future will resemble the past, or that the world is uniform in ways that can justify generalisations from observed instances to unobserved ones. These assumptions could only be supported by other inductive arguments, but then we’re in a vicious cycle of using induction to justify the use of induction. The assumptions necessary for us to believe in the conclusions of our inductive arguments imply epistemological crutches we rely on for psychological reasons. Contrary to popular opinion and our best wishes, without these grand assumptions about the world, induction never gives us any reason to think the conclusion of a strong inductive argument is made more probable by the premises that are given as evidence. This devastating critique of induction is owing to Hume.
Predictive Induction
We’ve come across predictive induction already when we talked about simple enumerative induction (some people call this a subcategory of inductive generalisation). Predictive induction is an argument where a conclusion about the future follows from our knowledge of the past. This form of reasoning draws a conclusion about the future using information from the past.
‘Predictive induction’: Inferring from known instances or cases to another future or unobserved instance or case.
We saw the general form above, so now for a concrete example:
In the past, ducks have always come to our pond.
The ducks will come to our pond this summer.
In contrast to generalisations, or the strong form of enumerative induction (and when I say strong here, I don’t mean it’s stronger in its inference or argument, but simply stronger in its claim – as in, it makes stronger claims), an inference isn’t made about a whole group or class, but just about the next instance of that group or class.
Every time I stop flossing my teeth, I start to develop gingivitis.
If I stop flossing again, I will develop gingivitis again.
We’ve also mentioned the problems with this type of induction many times, in that we can never know with any certainty what the future holds.
Cause and Effect
Rather than looking for patterns by way of enumerative generalisations, we often make inferences about cause and effect connections. Causal inductive reasoning is another common form of reasoning we use all the time without thinking about it. In fact, as I’ve mentioned at other times in this text, causality is always inferred (mostly inductively) and never directly observed. As a result, through repeated experiment, we build up plausible causal models that link events in our world.
A causal inference draws a conclusion about a causal connection based on the conditions of the occurrence of an effect. Premises about the correlation of two things can indicate only the possibility of a causal relationship between them – additional factors must be confirmed to offer any confidence in the existence of a causal relationship.
‘Causal induction’: Inferring from correlations (and additional premises) among known instances or cases to conclude a causal connection exists between them (i.e. that one of the events or instances causes the other).
The example below shows how a cause and effect argument can be used to make a predictive inference about a future case. Below, the first premise is an empirical premise that supports the causal inference to premise 2, which then is the warrant for inferring the conclusion. In this way, we can see how forms of inductive arguments can be combined or used to support each other.
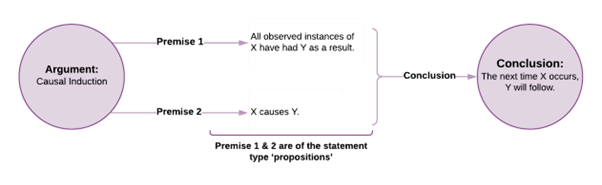
Causality isn’t so easily harnessed, though, and is just as complicated a notion to impose on our inductive reasoning as generalisations or the prediction of the future. For our inductive causal arguments to be compelling, we need some evidence that satisfies our concerns about other causes or reverse causation, as well as the sequence of events in time. When we fail to satisfy these other criteria, we’re at risk of committing a range of fallacies when we invoke cause and effect arguments in our inductive reasoning (e.g. historical fallacy, slippery slope, false cause, and confusing correlation and causation). We’ll look more at these in the next chapter. Identifying that two events co-occur or are correlated is a necessary condition for drawing a conclusion that there could be a causal connection between them because we can’t infer there is any causal connection for events that don’t have any co-occurrence or correlation. However, if you’ve heard the phrase ‘Correlation is not causation’, you should already understand that this co-occurrence or correlation is necessary, but not sufficient. Nothing is ever conclusively sufficient to confirm a causal link between events or things. The existence of causality is only ever an assumption that is plausible because we satisfy necessary conditions.
There are three necessary conditions that need to be met before we can consider a causal inference plausible. If any of these are not met, the inference to a causal connection is not yet plausible. However, they are not sufficient conditions in that meeting any one of them doesn’t give us any certainty about causality.
Our more accurate understanding of causality is once again due to Hume (as you can guess, I’m a big fan). If we’re true empiricists and truly only trust what we perceive with our senses, we’ve no right to any idea of causality, but rather we need to infer it rationally – that is, impose this idea on our understanding of the world. Seeing cause and effect all around us is like a mental habit, or one of those top-down processes on our perceptual experiences that produces an augmented reality. Cause and effect are always just a best guess or a compelling inductive inference.
The Four Types of Induction
The first thing I need to say is that the above list isn’t exhaustive, and so there are many other types of inductions and variants on these types. These four, however, are the ones I believe you’ll come across most in your daily life, in your science studies, and in confrontation with other people.
As you can see in Table 6.7 these types of induction not only have slightly different argument structures, but afford us different types of knowledge with different reach. This increasing reach must be paid for in ever shakier or more audacious assumptions (premises). The following table presents them from the simplest to the most difficult to establish. You’ll see the arguments get more and more powerful as they rely on more and more assumptions. In an ideal world, we would like to understand the causes of things and events, as this provides us with the most in-depth and useful information. This is why scientists are continually looking for the causes of things because once we know the causes of phenomena, we can explain, predict, and control them. Uncovering cause is the Holy Grail of science and the most difficult inductive argument to justify.
| AIM | Infer to…(read) | Needed Premises | Necessary/Unjustified Assumption |
| Predictive (weak enumeration) | The next instance of a class or population. | List of observed instances; Reasons to believe the future will resemble the past. | The future will resemble the past. |
| Generalised (strong enumeration) | All instance of a class or population. | List of observed instances; Reasons to think the sample is large, varied and representative enough. | The population resembles the sample (needs large, varied, random sample). |
| Analogous | A similar instance of a thing is already known/understood. | Establish compelling similarities between the known thing and the thing to be inferred about. | That the inferred similarities can be justified from the known similarities. |
| Cause and Effect | A casual connection between things and events. Consequently, infer the alleged cause producing the effect in the future. | Constant conjunction between cause and effect; Establish time sequence such that cause precedes effect (effects can’t happen before their causes); The elimination of rival candidates and other directions of casual influence (x causes y or y causes x or another variable z causes both). | That casual connections exist between things and events; That the direction of causality is known; That the specific cause is correctly identified (no confounds involved). |
Table 6.7. Features of Induction
Additional selection task-style puzzles to practice modus ponens and modus tollens.
Try solving these puzzles before seeing the answers below.
-
The Drinking Age Puzzle:
-
Four cards are placed on a table. Each card has an age on one side and a drink on the other. The visible faces show: 16, 25, Beer, Coke.
-
Rule: “If someone is drinking beer, then they must be over 18.”
-
Which card(s) must you turn over to test the rule?
- Answer: The “Beer” card (to confirm the rule using modus ponens) and the “16” card (to potentially falsify the rule using modus tollens).
-
-
The Pet and Treat Puzzle:
-
Four cards are placed on a table. Each card has an animal on one side and a treat on the other. The visible faces show: Dog, Cat, Bone, Fish.
-
Rule: “If an animal is a cat, then it gets a fish.”
-
Which card(s) must you turn over to test the rule?
- Answer: The “Cat” card (to confirm the rule using modus ponens) and the “Bone” card (to potentially falsify the rule using modus tollens).
-
Answers
Absolutely! Let’s break down how modus ponens and modus tollens help us solve these puzzles:
1. The Drinking Age Puzzle
- Rule: “If someone is drinking beer, then they must be over 18.”
- Cards: 16, 25, Beer, Coke
Modus Ponens (Affirming the Antecedent):
- To confirm the rule, we need to turn over the “Beer” card. The rule states that if someone is drinking beer (antecedent), then they must be over 18 (consequent). Finding an age over 18 on the other side of the “Beer” card would support the rule.
Modus Tollens (Denying the Consequent):
- To potentially disprove the rule, we need to turn over the “16” card. The rule implies that if someone is under 18 (not the consequent), then they cannot be drinking beer (not the antecedent). Finding “Beer” on the other side of the “16” card would violate the rule.
Why the Other Cards Don’t Matter:
- The “25” card is irrelevant because the rule doesn’t say anything about what people over 18 must drink. They could be drinking beer or coke without violating the rule.
- The “Coke” card is irrelevant because the rule only specifies the conditions for drinking beer, not other beverages.
2. The Pet and Treat Puzzle
- Rule: “If an animal is a cat, then it gets a fish.”
- Cards: Dog, Cat, Bone, Fish
Modus Ponens (Affirming the Antecedent):
- To confirm the rule, we need to turn over the “Cat” card. The rule states that if the animal is a cat (antecedent), then it gets a fish (consequent). Finding “Fish” on the other side of the “Cat” card would support the rule.
Modus Tollens (Denying the Consequent):
- To potentially disprove the rule, we need to turn over the “Bone” card. The rule implies that if an animal does not get a fish (not the consequent), then it cannot be a cat (not the antecedent). Finding “Cat” on the other side of the “Bone” card would violate the rule.
Why the Other Cards Don’t Matter:
- The “Dog” card is irrelevant because the rule doesn’t state what treats dogs receive. They could be getting a bone, fish, or something else without violating the rule.
- The “Fish” card is irrelevant because the rule only specifies the treat for cats, not which animals might receive fish.
In both puzzles, the key to solving them lies in correctly applying modus ponens and modus tollens to identify the cards that are relevant to testing the rule.
Additional Resources
 By scanning the QR code below or going to this YouTube channel, you can access a playlist of videos on critical thinking. Take the time to watch and think carefully about their content.
By scanning the QR code below or going to this YouTube channel, you can access a playlist of videos on critical thinking. Take the time to watch and think carefully about their content.
Further Reading:
- Summary article for deductive syllogisms: Lander University. (n.d.). Introduction to logic. In Philosophy Course Notes. Retrieved December 8, 2022. From https://philosophy.lander.edu/logic/prop.html#:~:text=Quantifier%20%5Bsubject%20term%5D%20copula%20%5Bpredicate%20term%5D.&text=Quantity%2C%20and%20Distribution-,A.,universal%20or%20particular%20in%20quantity
- Master syllogisms: wikiHow Staff. (2020). How to understand syllogisms. In wikiHow. Retrieved December 8, 2022, from https://www.wikihow.com/Understand-Syllogisms
- Wikipedia. (n.d.). Affirming the consequent. Retrieved December 8, 2022, from https://en.wikipedia.org/wiki/Affirming_the_consequent#:~:text=Affirming%20the%20consequent%2C%20sometimes%20called,is%20dark%2C%20so%20the%20lamp. Used under a CC BY-SA 3.0 licence. ↵
- Coles, P. (2019, April 15). Einstein, Eddington and the 1919 eclipse. Nature. https://www.nature.com/articles/d41586-019-01172-z ↵
- For those who are curious, the baby is a rambunctious little boy named Jack. ↵
- Discussion based on Rudolf Carnap's taxonomy of the varieties of inductive inference: Hawthorne, J. (2012). Inductive logic. In Stanford Encyclopedia of Philosophy Archive, Summer 2016. Retrieved December 8, 2022, from https://plato.stanford.edu/archives/sum2016/entries/logic-inductive/ ↵
- Salmon, W. C. (1984). Logic (3rd ed.). Prentice-Hall. ↵
- Wikipedia. (n.d.). Inductive reasoning. Retrieved December 8, 2022, from https://en.wikipedia.org/wiki/Inductive_reasoning#Argument_from_analogy ↵

